大模型与无限猴子定律——复杂推理的Repeated Sampling Scaling Law

本文链接：https://blog.csdn.net/qq_36426650/article/details/142471776

Large Language Monkeys: Scaling Inference Compute with Repeated Sampling

Github：https://github.com/ScalingIntelligence/large_language_monkeys

无限猴子定律也被称为猴子和打字机定理，是一个概率论中的概念，用于阐述随机性和概率的问题。这个定律的基本思想是：如果有一大群猴子随机地敲打打字机的键盘，那么理论上，只要时间足够长，它们最终会打出任何给定的文本，包括莎士比亚的全部著作。

提升训练规模和资源有助于LLM的性能，然而在推理（Inference）阶段则通常计算资源很有限，因此本文旨在探索Inference阶段的对生成的sampling数量进行scaling。对于SWE-bench Lite，如果进行repeated sampling 250次，相比于只生成一个sample，性能可以从15.9%提升到56%。此外，按照当前的 API 定价，使用五个样本来放大更便宜的 DeepSeek 模型比为 GPT-4o 或 Claude 3.5 Sonnet 中的一个样本支付额外费用更具成本效益，并且能解决更多问题。有趣的是，覆盖率和样本数量之间的关系通常是对数线性的，可以用指数幂律建模，这表明推理时间缩放定律的存在。

Scaling Repeated Sampling

目前在Inference阶段探索the amount of computation 还相当有限，大模型在推理时可以通过CoT的形式增加生成的token数量来提高结果的质量。本文则通过探索Repeated Sampling，常识增加采样推理的数量来提高效果。

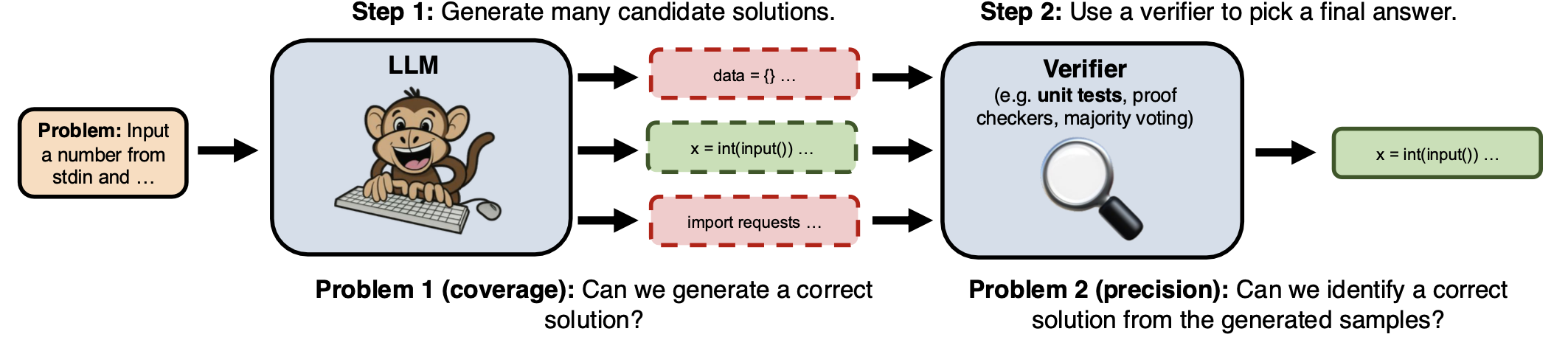
主要流程如上图所示：

首先让一个LLM多次采样生成（上百次），从而尽可能覆盖到正确答案；
其次如何获取一个Verifier并找到这个正确答案。

因此，Repeated Sampling主要建立在如下两个keynote：

Repeated Sampling需要建立在一个可接受的预算范围内执行

例如在CodeContests任务上采用Gemma-2B模型，随着采样生成样本数量的增加（一次生成 -> 10000次生成），覆盖率提高了 300 多倍（ 0.02% -> 7.1%）

为了加速推理，菜哟过vLLM进行Repeated Sampling

考虑的复杂推理任务包含如下5个：

验证LLM性能的一个指标是任务解决的success rate，即Pass@K（覆盖率）。Pass@K的无偏估计定义为：给定一个prompt $i$ ，对应 $N$ 个采样生成样本，正确的样本有 $C_i$ 个，那么Pass@K为：

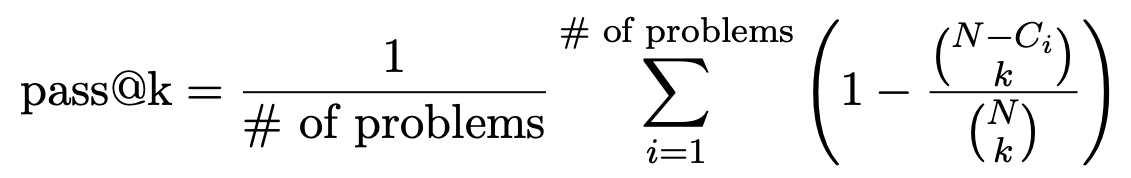
通过在5个不同的推理任务上实验，发现采样数量$ N $与Pass@K存在近乎log线性的关系，如下所示：

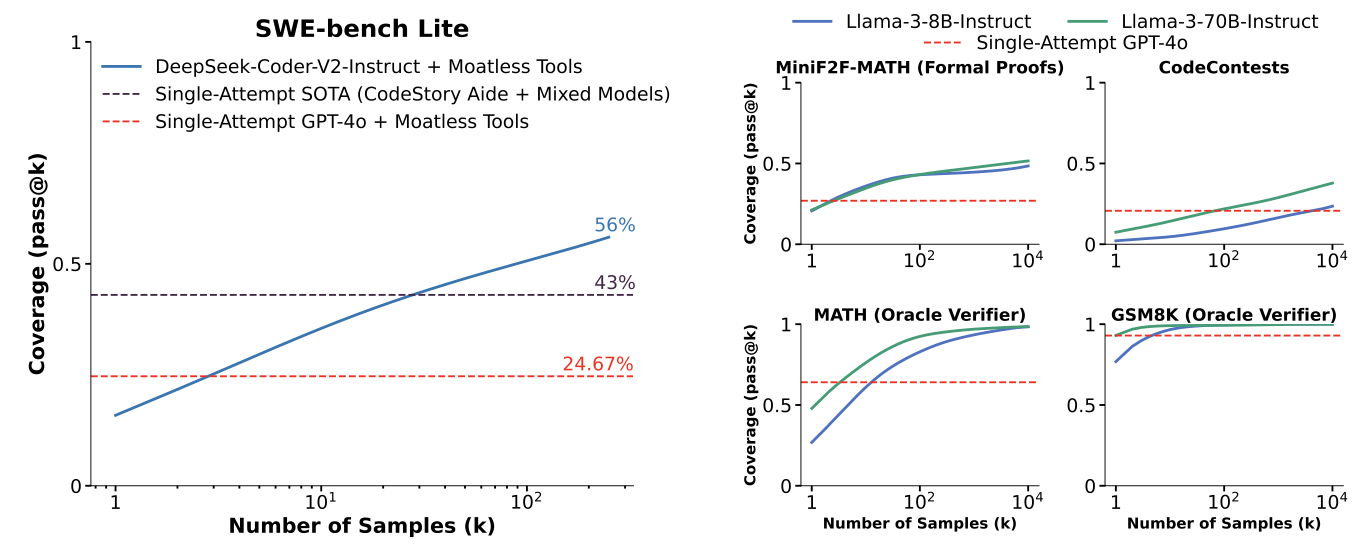
而且不论模型的规模有多大（最小70M，最大70B），这种log线性关系一直都符合，如下图所示：

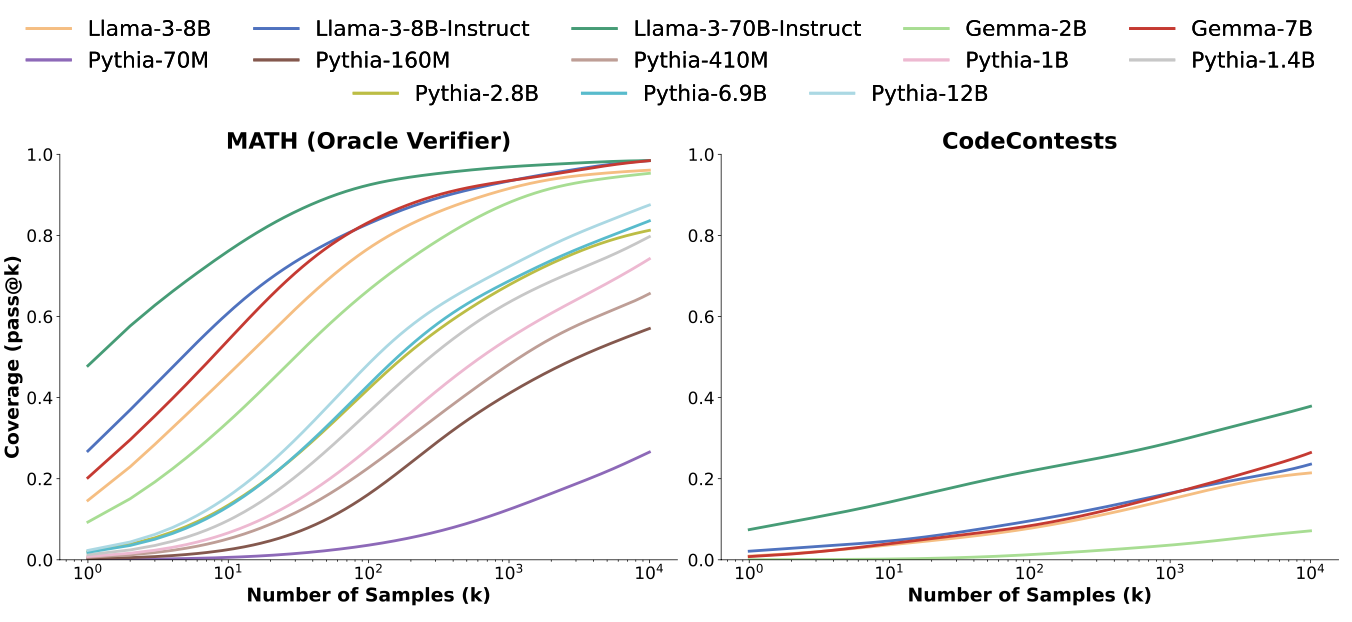
针对Weak LLM进行Repeated Sampling在消耗预算（Cost Budget）上优于Strong LLM。选择FLOPs作为计算消耗指标。总的FLOPs计算可估计为：

Pass@K（覆盖率）于FLOPs的关系如下所示：

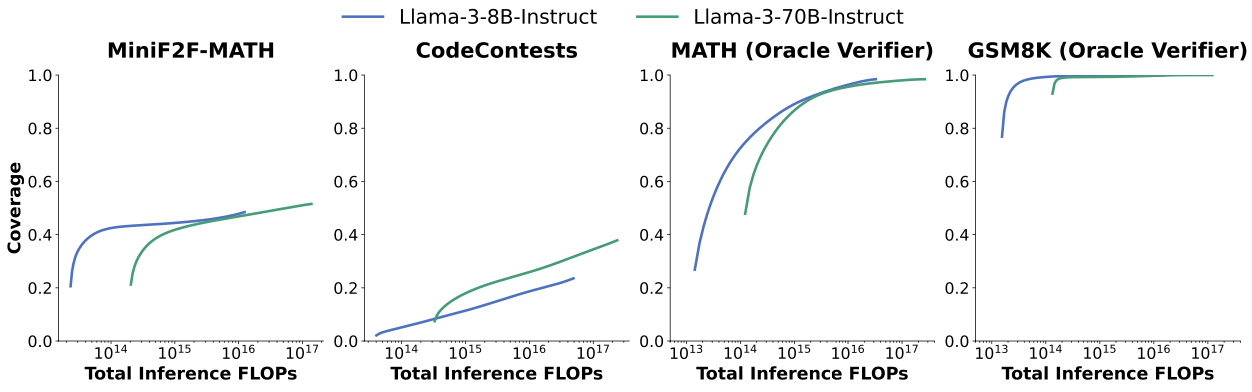
可以发现，在MiniF2F-MATH、MATH和GSM8K任务上，达到相同覆盖率下的FLOPs计算量8B模型远远低于70B模型，这说明Weak LLM在Cost Budget上优于Strong LLM。

从API费用开销来看（如下表所示），较小的模型（DeepSeek）在进行5次Reapted Sampling所需要的开销低于仅一次生成的GPT-4o，且效果反而更好。

Characterizing Repeated Sampling

先上结论：

Repeated Sampling中，Pass@K覆盖率于采样生成的数量满足指数幂律（exponentiated power law）
对于给定的任务，同一系列的不同模型的覆盖曲线类似于 S 曲线，具有相似的斜率但不同的水平偏移。

首先定义Pass@K（coverage）的Power Law： $\log(c)\approx ak^{(-b)}$ ，并可以变换为 $\c\approx \exp (ak^{(-b)})$ 。

不同规模类型的模型在MiniF2F-MATH任务上的Pass@K-K曲线与标准Power Law曲线的重合程度情况如下图所示：

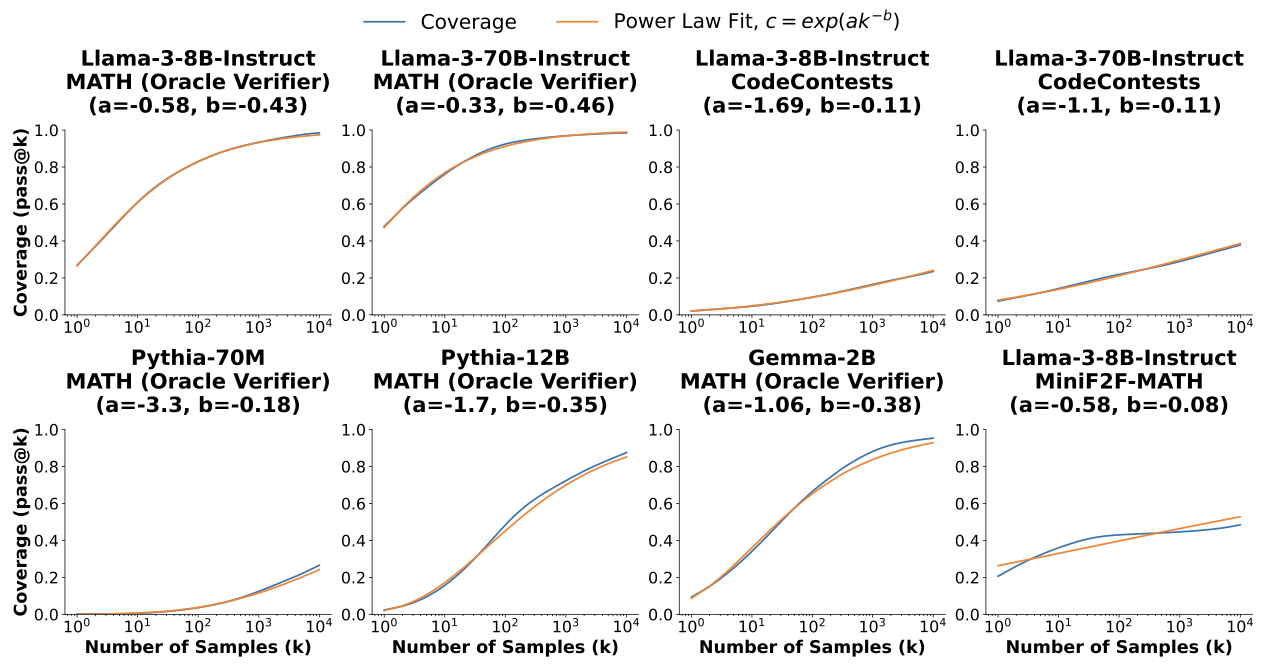
可发现Pass@K-K曲线几乎与Power Law曲线相吻合。

另外，根据之前的观测结论，Pass@K与采样生成的数量存在log线性关系。不过可以发现，不同类型的模型对应的斜率（ $a$ ）和指数（ $- b$ ）各不相同。但是，相同类型的模型不论规模多大，对应斜率和指数大致相同，且都呈现相似的S形。

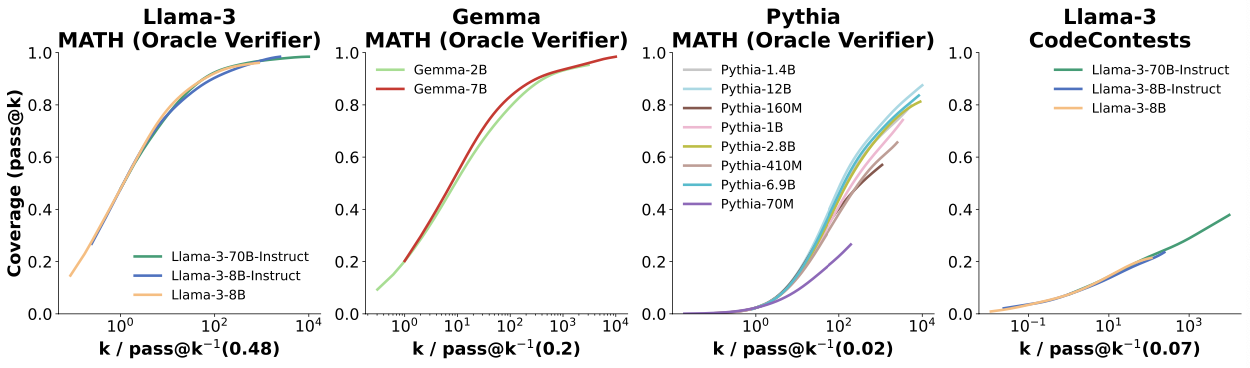
Difference Verifier Don’t Scale Repeated Sampling

Pass@K是指被采样中的样本正确的无偏估计，那么如何挑选出这些正确的采样生成样本呢？这里有三种方式：

Majority Vote：挑选结果一致最多的答案，等价于Self-Consistency；
Reward Model + Best-of-N：对所有样本进行打分，并取得分最高的答案；
Reward Model + Majority Vote：基于Reward分数加权求和后，分数最高的且结果一致的答案；

如下图所示，可以发现，三种Verifier都不满足Scaling Law

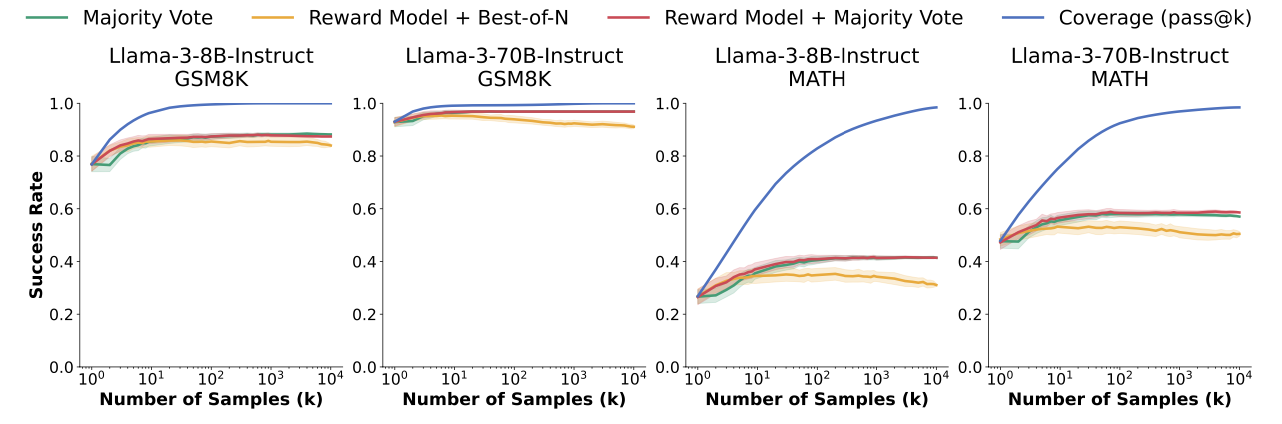
其次，探索不同模型在GSM8K和MATH上进行10000次Reapted Sampling过程中正确的CoT数量，如下图：

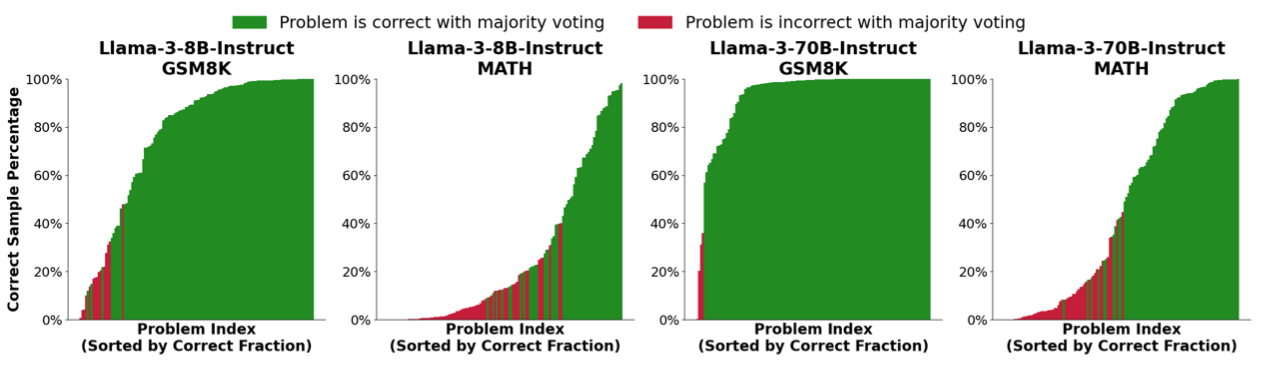
绿色表示10000次采样中通过Majority Vote得到的答案正确的比例，可发现投票数达到一定比例时几乎都是正确。

Improvement Repeated Sampling

如何利用Repeated Sampling来提高LLM推理能力呢？

Solution多样性：通过结合采样策略（例如temperature）与其他方法来增加推理过程的多样性；
多轮交互：通过多轮交互的形式引入环境工具反馈信息，可以提高solution的质量，这样虽然每一次采样生成变成多轮模式，但是在相同覆盖率条件下采样生成的次数可以大大降低；
Learning From Previous：基于已有的采样生成样本，通过Verifier获得反馈，来帮助更好地完成下一次采样生成。