论文翻译：The basic physics of the binary black hole merger GW150914（引力波发现的那双黑洞的基本物理性质，2016.10.4发表）

妖歌长安

于 2020-02-06 22:56:40 发布

阅读量1.1k

点赞数 3

分类专栏：天体物理翻译

天体物理同时被 2 个专栏收录

3 篇文章 0 订阅

订阅专栏

翻译

2 篇文章 0 订阅

订阅专栏

摘要：2015年9月14日，LIGO第一次探测到了GW（一个恒星级双黑洞）的引力波信号，给爱因斯坦广义相对论预言强有力的证明。信号被LIGO两个探测器（LA和WA，简写）探测到。而提取关于源的全部信息需要更深入的分析方法和计算机算法。然而，对于普通人来讲可以从这次直接观测中知道更多。这个简单的分析表明信号源时两个互相绕转的黑洞并且合并形成了另一个黑洞。

黑洞是时空的奇点其引力场强到以至于没有任何物质或辐射可以逃离。与质量相关的引力半径我们称为施瓦西半径：

$r_{Schwarz}(m)=\frac{2Gm}{c^2}=2.95(\frac{m}{M_\odot})Km$

其中 $M_\odot=1.99\times10^{30}kg$ 表示太阳质量， $G=6.67\times10^{-11}m^3/s^2kg$ 表示牛顿引力常数， $c=2.998\times10^{8}m/s$ 是光速。根据环猜想（百度：一个物体，当它经历高度非球形压缩时，只有当它在各个方向的周长都小于临界周长时，它才会形成黑洞），当一个非自旋物体被压缩至小于施瓦西半径，那它一定会形成黑洞。一旦黑洞形成，在半径以内的东西就再也逃不出去了。

从仪器的可见数据以及一系列分析（主要是牛顿轨道动力学和引力波源光度的爱因斯坦四极矩公式）可得GW（看见GW当信号就ok）是由两个黑洞的激发和合并产生的。这些计算太简单直接以至于能用笔一会就可以验证。我们的内容通过巧妙近似来强调简单的论点。

尤其是当两个物体的轨道运动在足够远的间距与足够低的速度下用牛顿动力学和开普勒定律来近似，即使在轨道末端的运动我们仍然用牛动力学来描述。广义相对论的完全非线性理论能让牛顿力学分析彻底失效，然而，爱因斯坦方程的数值解表明双黑洞系统的分离直到演化后期都可以从牛顿力学用有限微扰分析法解释我们的观点。

这里介绍的用基本物理的方法作为一种使用直观但粗略的方法来建立直觉的工具，更接近于教学形式介绍引力波信号的物理意义。这里的讨论是有设计基础的，但是给出的结果与高级处理方法一致。完整严格的过程包括描述系统的精确数字以及发表在其他地方了。

论文的结构如下：讨论从探测器的数据开始，第二部分是从应变数据读取的信号属性，还有他们如何给出与双星激发系统有关的性质。第三部分我们就用最简单的假设讨论为什么双星构成必须又致密又小，与之符合只有黑洞。第四部分就是测试和验证受约束的质量必须远大于已知最重的中子星。第五部分是用引力波峰值光度来估计我们到源的距离，并计算系统的总光度。

第二部分：观测数据分析

我们从图1开始看，仪器观察到的应变数据是 $h(t)$ ，将带通滤波器用到LIGO的敏感频率带（35-350 Hz），带阻滤波器用到仪器噪声上。信号的时频行为在图2。也可以直接从图1的应变数据通过测量连续过零点的 $\Delta t$ 并估计引力波频率 $f_{GW}=1/(2\Delta t)$ 直接获得时频演化形式，而且没有假定波形模型。我们画了频率的 $f_{GW}^{-8/3}$ 图并解释了它的物理意义。

Figure 1.两个探测器信号数据（蓝的是L1，红的H1），两组信号都经过了带通滤波器处理的，H1的数据是经过6.9ms向前时移和反向处理的。

Figure 2 用时频图来表示应变数据，其中信号随频率的增加可以沿时间追踪到。

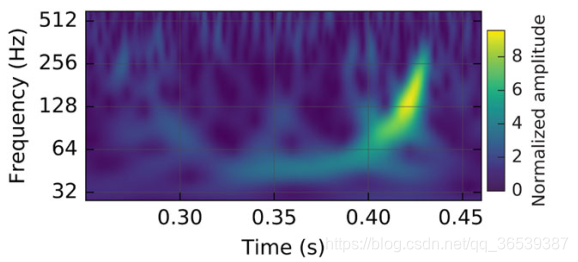
从0.3s开始，振幅开始增加的信号由波形的多个周期主导。这段时间内引力波周期的减少即频率的增加。在0.42s附近，信号振幅迅速下跌，而频率趋于稳定。最后一次可见周期显示瞬时频率超过了200Hz。整段可见信号部分持续了大约0.15s。

按广义相对论，引力波是物体加速产生的。由于波形显示了至少8个振荡，我们知道那儿是一个或多个物体在振荡。引力波频率和振幅的增大表明源系统的振荡频率也在增大。这样的初始行为并不是由于受扰系统返回平衡位置导致，因为平衡位置的振荡一般有大致的频率常数和衰减振幅为特征。比如在圆球绕流（流体绕圆球体的流动）情况下，振动会被粘性力衰减。

在引力波频率振幅增加过程中，两个物体的轨道行为的唯一的合理解释：唯一的阻尼力由引力波辐射提供，它使得两物体轨道越来越近（也可以叫特殊的“激发过程”），也增大了轨道频率和系统的引力波能能量。（我好奇自己的辐射使得自己的获得的能量增加，真神奇。）

引力辐射在加速电荷方面与电磁场有很多类似的地方。一个重要区别是没有与电磁偶极辐射类比量，电磁偶极辐射的振幅与偶极矩的二阶时间导成正比。这是因为引力模拟是质量偶极矩（ $\sum m_AX_A$ 以速度）的时间一阶导是封闭系总线性动量守恒量，其二阶导因此就是0了。因此按优先顺序，引力辐射是四极矩的。因为四极矩在围绕轨道轴旋转 pi 后是对称的，且辐射频率是轨道频率的2倍（具体计算在附录）。

8个频率逐渐增大引力波信号周期要求至少4次轨道公转，而且离得足够远到不会碰撞（要相比于物体本身大小）。频率停止增大表明轨道的激发停止了。当振幅衰减频率稳定系统回到稳定位置。我们将给出唯一合理的频率演化观测解释是系统由两个互相绕转的黑洞组成并之后合并的结果。

确定最大压力振幅处的频率为 $f_{GW}|_{max}$ ：本论文中信号最重要的一个推理量就是波形在最大振幅处的引力波频率。用图1峰值附近的零轴交点和图2最亮的点，我们取保守值：

$f_{GW}|_{max}\sim 150Hz$ (2)

这里和其他地方的垂线前符号是用来表示对线后的那个时间点进行估计（意思就是垂线前那个字符是垂线右下角那个代表时间处的估计值）。我们因此呢插入观测数据来表示物体在以一个轨道角频率互相绕转

$w_{kep}|_{max}=\frac{2\pi f_{GW}|_{max}}{2}=2\pi \times 75 ~Hz$ (3)

Fig 3 绿线是对频率 f-{GW}^{-8/3}(t)的线性拟合。虽然插值用到了组合H1和L1的应变数据（实际上就是之前解释的L1的时移和信号翻转）。类似的用H1或者L1的应变数据都可以做到独立拟合。拟合的残差平方和为 R^2~0.9，同时H1与L1的独立残差平方和为 R^2_{H1}~0.9、R^2_{L1}~0.8。用公式8代入拟合曲线的斜率给出 chirp mass 的估计值大约37个太阳质量。蓝色和红色线分布的 chirp mass 值为30倍太阳质量和40倍太阳质量。通过在GW信号之前给LIGO中加入相同振幅和频率的波形，再重复上述步骤（也就是插值法算残差吧）就可以得到误差曲线。使用H1和L1的零轴交点差异可以得到相似结论。

确定质量范围：爱因斯坦发现在离系统 $d_L$ 远的引力波应变值 $h$ 的质量四极矩 $Q_{ij}$ 定义为：

$h_{ij}=\frac{2G}{c^4d_L}\frac{d^2Q_{ij}}{dt^2}$ （4）

引力波的带出能量率由四极矩公式给出：

$\frac{d E_{GW}}{dt}=\frac{c^3}{16\pi G}\iint\dot{|h|}dS=\frac{1}{5}\frac{G}{c^5}\sum_{i,j=1}^{3}\frac{d^3Q_{ij}}{dt^3}\frac{d^3Q_{ij}}{dt^3}$ (5，顺带一句我没抄错)

其中 $\dot{|h|}^2=\sum_{i,j=1}^{3}\frac{dh_{ij}}{dt}\frac{dh_{ij}}{dt}$

积分遍及整个半径为 $d_L$ 的球壳，右侧的值必须在一条轨道上积分取平均值。

在这个积分5式中，给出了轨道能量给引力波的效率，其中轨道上物体的速度与光速很不接近，而且应力也不是特别大；我们会反复用它（指公式5）直到频率 $f_{GW}|_{max}$ 求出来。这个波的描述适用于弱引力场和宇宙膨胀可忽略的波形区域。

对于双星系统我们用 $m_1$ 和 $m_2$ 表示质量，总质量就是 $M=m_1+m_2$ ，折合质量就是 $\mu =m_1m_2/M$ 。定义质量比 $q=m_1/m_2$ 在不失一般性的假设 $m_1\geq m_2$ ，这样的话 $q\geq 1$ 。为了描述系统发出的引力波，一个有用的质量物理量就是chirp mass $\texttt{M}$ ，通过下式与质量分量联系在一起

$\texttt{M}=\frac{(m_1m_2)^{3/5}}{(m_1+m_2)^{1/5}}$ (6)

对系统的引力波光度用牛顿运动定理和牛顿引力公式以及爱因斯坦四极矩公式，与频率和引力波的频率导数有关的chirp mass $\texttt{M}$ ：

$\texttt{M}=\frac{c^3}{G}((\frac{5}{96})^3\pi ^{-8}(f_{GW})^{-11}(\dot{f}_{GW})^3)^{1/5}$ (7)

其中 $\dot{f}_{GW}=d~f_{GW}/dt$ 表示频率变化率。这个公式只要牛顿近似成立那么它就成立。

因此呢，chirp mass 的取值直接取决于观测数据，用任意时刻的引力波频率和频率的导数就可以。比如频率就可以从图二的时频图中预测，对于频率导数则可以通过画时频图的切线得到。时间间隔是在探测器的敏感波段对应于引力波在频率 $30<f_{GW}<150 ~\texttt{Hz}$ 范围内。经过这段时间，频率变化了 5(1/5) 倍（这儿不会读），而频率导数则变化超过2个数量级。然而对于 chirp mass 值，仍然保持在常值的35%以内，精确值我们这里没有严格讨论，所以为了简单起见取了 $\texttt{M}=30M_{\odot}$ 。

要注意辐射系统的质量范围的特征是通过观测数据的时频情况直接获得的。

在频率 $f_{GW}<150 ~\texttt{Hz}$ 时 chirp mass 近似保持恒值为轨道解释提供了强有力支持。引力波的应变振幅随频率的增强而增强也支持了这一解释，表明计算得出这些公式用的那个假设是适用的：双体系统的速度不能太接近于光速且轨道行为有绝热变化的半径和开普勒瞬时周期（这个绝热变化的半径没查到什么意思）。观测数据也表示随着振幅停止增加，当引力波频率大于 $f_{GW}|_{max}$ 时假设就失效了。

或者公式7可以整合得到：

$f_{GW}^{-8/3}(t)=\frac{(8\pi)^{8/3}}{5}(\frac{G\texttt{M}}{c^3})^{5/3}(t_c-t)$ (8)

其中并没有显含 $\dot{f}_{GW}$ ，这公式也可以用来从应变数据的零点间时间周期直接计算 chirp mass $\texttt{M}$ 。积分常数 $t_c$ 是合并时刻，我们进行了图3这样的分析来寻找类似的结论。之后我们就对 chirp mass 就保守估计为 $\texttt{M}=30M_{\odot}$ 。我们注意到这个质量值是从探测器测量的那些值中得到的，因此它和其他值都是我们从探测器中得到的。

3 最简单情况下致密性的证据

最简单情况，我们假设两个物体质量相等 $m_1=m_2$ 。那么 chirp mass 意味着 $m_1=m_2=2^{1/5}\texttt{M}=35M_{\odot}$ ，因此呢总质量就会变成 $M=m_1+m_2=70M_{\odot}$ 。我们还假设物体没有自旋，且轨道在到达振幅峰值前（我：峰值就是双星合并了）依然符合开普勒定律和圆形轨道。

因此在峰值附近的双星间距 $R$ 由下式给出：

$R=(\frac{GM}{w^2_{kep}|_{max}})^{1/3}=350\texttt{km}$ (9)

与恒星的轨道间距尺寸相比这算是很小的值了。这就限制该星体要极其的小否则在到达这么近距离前就会撞击或者合并。主序星的轨道半径在几百几千或者几百万公里，白矮星轨道的半径一般是几万公里。尺度公式（9）表示这类恒星的激发演化将随着轨道频率低到几个 mHz 时合并而终结。

目前已知最致密的恒星就是中子星了，其半径就是十几公里。两个中子星可以在这么近距离下不碰撞绕行或者合并，但是合并成一个黑洞前一个中子星质量最大大约是 $3M_{\odot}$ 。

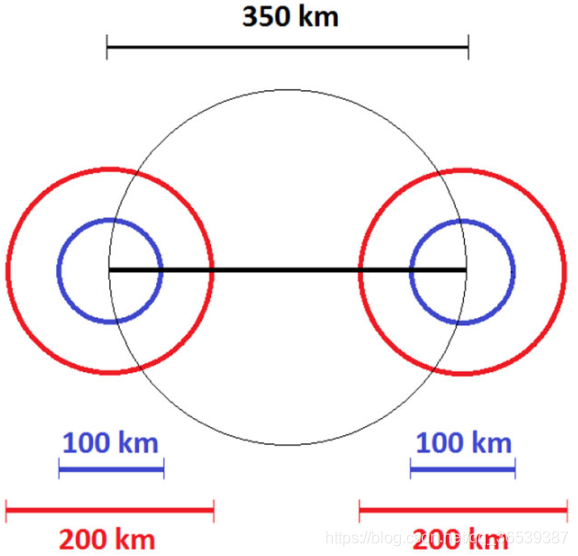
在我们的情况里两个星体质量 $m_1=m_2=35M_{\odot}$ ，且各自对应的施瓦西半径为 103 km。这些在图4中由解释。两星体轨道间距是 350 km ，仅仅大约是他们施瓦西半径和的二倍。

为了量化两星体相对于其引力半径的的接近程度（我有点懵），我们引入紧密率参数 $\mathfrak{R}$ ，它被定义为中心两天体间牛顿轨道半径比上各自最小半径之和。对于我们刚讨论的等质量、非自旋和圆轨情况， $\mathfrak{R}=350\texttt{km}/206\texttt{km} \sim 1.7$ 。

Figure 4 最小间距下的轨道大小（黑的，350km）与紧密星体半径：施瓦西半径（红的，200km那个）还有克尔半径（蓝的，直径100km那个）的对比。注意这里两星体质量相等，若质量不相等那么系统还会更加致密。然而相对论里测量点和点之间距离的刚性参考系并不唯一，这种复杂性只有在强引力场中才会出现，而在开普勒情况下（也就是低致密和弱引力势情况）下系统的质心相对静止参考系就可以用。因此呢，如果系统明确是非致密的，那么就可以拿开普勒情况讨论就站得住脚，而且要限制间距防止模型致密。于是非致密的概率与数据是不吻合的。

与其他开普勒系统相比，太阳系最里边的水星的 $\mathfrak{R} \sim 2\times10^7$ ，对于天鹅座那个恒星级双黑洞 X-1 的 $\mathfrak{R} \sim 3\times10^5$ ，已知的双黑洞系统最高频率是在双白矮星 HM Cancri (又名 RX J0806,最短周期的双星系统)其紧密率参数 $\mathfrak{R} \sim 2\times10^4$ 。围绕我们的银河系中心的轨道观测表明存在一个超级黑洞起名叫 $\texttt{Sgr A*}$ (又名天马座A*)，恒星 S2 紧绕着它转对应的参数 $\mathfrak{R} \sim 10^3$ 。对于双中子星系统其紧密率参数将介于 $\sim 2$ 和 $\sim 5$ 之间（这他妈也太近了，NB）。

GW的信号的轨道推断间距是黑洞半径量级时更进一步证明两物体的高度致密性，在牛顿或者开普勒演化理论里失效了。

4 回顾假设

我们在第3部分用数据展示了圆轨假设下合并情况得是无自旋的黑洞才行。但用这种程度的近似直接去限制这些系统的参数是这不可能的（尽管我们有更先进的技术来限制参数）。然后，研究这些假设是如何影响我们结论还是可能的，这一小节部分我们将展示不限制这些参数也不会对结果有影响。我们也用了开普勒近似来讨论这三种模型（4.1-4.3），然后重新回顾开普勒近似本身并讨论前述的结果（4.4-4.5部分）。在4.6我们讨论离源的距离和其是能影响。

4.1 轨道偏心率

对于非圆形轨道的离心率 $e>0$ ,开普勒第三定律中的 R 不再只代表轨道距离，也代表半长轴（椭圆的）。瞬时轨道距离 $r_{sep}$ 上界由半长轴 R 限制，下界由近心点（类似于咱们的近日点）限制，即 $r_{sep}\geq (1-e)R$ 。因此偏心轨道限制的致密边界更加紧密了（致密率 $\mathfrak{R}$ 更小了）。

对偏心率依赖的光度进行了修正，但是修正仅对高偏心率轨道起作用（原因是：偏心率与光度关系是 $\mathfrak{l}(e)=(1-e^2)^{-7/2}(1+\frac{73}{24}e^2+\frac{37}{96}e^4)\geq 1$ ，因此呢公式7减小 chirp mass 到 $\texttt{M}(e)=\mathfrak{l}^{-3/5}(e)\cdot \texttt{M}(e=0)$ 。代入计算轨道间距在近心点值与半长轴的比，就能得到 $\mathfrak{R}(e)=(1-e)\mathfrak{l}^{2/5}(e)\cdot\mathfrak{R}(e=0)$ 。因此呢致密率增加，离心率一定 $e\gtrsim 0.6$ ，如果致密率增大2倍 $e\gtrsim 0.9$ ，见图5）。对于这些，信号应该显示出调制：近心点速度大于远心点速度，所以信号就会在最高最低振幅间来回。而这种调制并没有出现在数据中，信号振幅反而单调递增。

这并不惊奇，当引力波带着动量离开导致轨道趋向圆形速度要比其轨道收缩要快。这个修正可以忽略（嗷~~，可以忽略）。

4.2 质量不相等情况

很容易得到随着质量比增加，致密率在变小，因为那意味着观测到更大的 chirp mass 总质量。为了清楚认清这一点，我们用 chirp mass 和质量比 $q$ 表示出各自质量和总质量， $m_1=\texttt{M}(1+q)^{1/5}q^{2/5},m_2=\texttt{M}(1+q)^{1/5}q^{-3/5}$

$M=m_1+m_2=\texttt{M}(1+q)^{6/5}q^{-3/5}$ (10)

致密率 $\mathfrak{R}$ 是轨道间距 R 和两星体的施瓦西半径和比值，即 $r_{Schwarz}(M)=r_{Schwarz}(m_1)+r_{Schwarz}(m_2)$ ，有了下式：

$\small \mathfrak{R}=\frac{R}{r_{Schwarz}(M)}=\frac{c^2}{2(w_{kep}|_{max}GM)^{2/3}}=\frac{c^2}{2(\pi f_{GW}|_{max}G\texttt{M})^{2/3}}\frac{q^{2/5}}{(1+q)^{4/5}}\approx \frac{3.0q^{2/5}}{(1+q)^{4/5}}$ (11)

这个值在图5中画出来了，清楚的展现质量比 $q>1$ 时致密率在减小：以半径总和为单位衡量的星体间距变的更小了。因此对于给定 chirp mass 和轨道频率，由质量不相等组成的系统比质量相等的系统要更加致密。

纯粹在数据的基础上， $m_2$ 规定一个小一点的边界，对质量比就有了上限。这个边界来自最小的致密值：从图5的致密率图上我们发现在超过质量比 $q\sim13$ 时系统变得太致密以至于处于两星体总质量的施瓦西半径内。这就告诉我们得给小质量星体一个质量限制即 $m_2\geq 11M_\odot$ 。由于这比中子星质量极限的 3-4 倍还多，因此两个星体都有可能成为黑洞。

Figure 5 这个图显示了致密率限制了双星系统 chirp mass =30 M_sun和 f_GW|_max=150 Hz。致密率作为质量比和离心率函数的图像，离心率从0到0.8。左下角（q=1，e=0）相当于第3部分的情况。如4.1部分解释那样，修正质量比后系统会随着离心率增加变得更加致密直到离心率 e=0.27。底部 e=0 则解释了4.2讨论的情况和公式11：系统会送质量比增加而更加致密。我们也注意到对于 e=0下，若质量比 q>13时，系统会变得比施瓦西半径还小。

4.3 自旋效应

我们第三个剩余的假设涉及到物体的自旋，对于质量 m 的物体自旋角动量 S ，我们定义无量纲自旋参数：

$\small \chi =\frac{c}{G}\frac{S}{m^2}$ (12)

$\small m_1$ 与 $m_2$ 的自旋会调整引力半径和轨道动力。

对于无自旋 $\small \chi =0$ 的非黑洞星体其最小半径是其施瓦西半径。物体有自旋后其角动量会将最小半径减小2倍（意思是变成1/2？）达到 Kerr 黑洞半径的极限（ $\small \chi =1$ ），即 $\small r_{EK}(m)=\frac{1}{2}r_{Schwarz}(m)=Gm/c^2$ 。当其正比于质时，将半径线性相加我们得到一个非黑洞的相邻天体总质量为 $\small M$ 的牛顿间距更低的极限值：

$\small r_{EK}(m_1)+r_{EK}(m_2)=\frac{1}{2}r_{Schwarz}(M)=\frac{G~M}{c^2}\approx 1.5(\frac{M}{M_\odot})~~\texttt{km}$

致密率也可以用比 $r_{Schwarz}$ 更好的 $\small r_{EK}$ 来定义，与非旋转情况性比其致密率最大要大两倍。

我们也可以用下式来约束轨道紧密性（现在我们把离心率和质量不相等情况和自旋考虑进来）：

$\mathfrak{R}=\frac{r_{sep}(M)}{r_{EK}(M)} \leq\frac{R(M)}{r_{EK}(M)}=\frac{c^2}{(GM_{wkep})^{2/3}}\leq\frac{c^2}{(2^{6/5}G\texttt{M}f_{GW}|_{max})}\simeq 3.4$ (14)

其中最后一步用到了 $\texttt{M}=30M_{\odot}$ 和 $f_{GW}|_{max}=150\texttt{Hz}$ 。这就将间距限制在极限kerr半径的3.4倍以下，使其变得极其致密，致密机构图在图4中有解释。

由限制条件致密率必须大于1，我们就得到质量比q的上限。这是因为修正后的 chirp mass 和轨道频率 $f_{GW}|_{max}$ ，致密率随着质量比增加而减少。因此致密率 $\mathfrak{R}\geq 1$ 时给了质量比 $q$ 最大值限制，因此对于最大总质量有：

$(\frac{M_{max}}{\texttt{M}})\simeq 3.4^{3/2}\times2^{6/5}\simeq 14.4$ (15)

对于GW则代表 $M_{max}\simeq 432M_{\odot}$ （以及 $q\simeq 83$ ）。这就又限制了较小星体的质量至少要 $5M_{\odot}$ 高于中子星的质量极限。

结论与等质量情况和非自旋情况一样：俩星体必须是黑洞

4.4 牛顿动力学和紧密性

我们现在来检验牛顿动力学的可行性。当相对速度接近光速时动力学或者引力势能与物体静能相对比时将不能用牛顿动力学。对于由引力维持的双星系统和轨道速度为 $v$ ,这俩限制是一致的而且可以通过后牛顿参数 $x=(v/c)^2=G~M/(c^2r_{sep})$ 来量化。对牛顿动力学的修正或许可以用 x 的幂级数展开，并用其后牛顿值量级来对修正进行枚举（不知道在干嘛我）。在 x=0 处后牛顿近似是很精确的，其中动力部分是牛顿动力学和引力波辐射用四极矩公式5描述的很准确。

后牛顿参数的表达式包含了施瓦西半径，所以参数 x 会由于致密率改变而立即改变，因为 $x\sim(2\mathfrak{R})^{-1}$ 。当 x 足够小是牛顿动力学是成立的，而牛顿近似在直到几个数量级的致密率 $\mathfrak{R}$ 时都是有效的。运用反证法，一旦假设轨道是非致密的，那么我们对数据用牛顿力学的分析就被证明是广义相对论的近似并导出轨道是致密的结论。

如果两个星体都在快速自旋，其旋转速度又接近光速，就要增加自旋-轨道作用和自旋-自旋作用来修正牛顿动力学。然而这些修正都会随着后牛顿参数的幂级数而受到压制（分别是1.5PN 和 2PN ；意思大概是修正作用因为这俩量级不是很大吧），因此仅对致密轨道有意义。

同样的理由也可以用到四极矩公式15上面或者用坐标 R 来将开普勒间距和致密半径来比较时候用牛顿动力学来修正，当他俩都不完全适用或者可能错误时就可以用。而星体间距也受到规范自由度的限制。这里也一样，用这些坐标时的错误只要在轨道很接近于黑洞时才是不可忽略的，所以再一次论点不违反我们的结论。

4.5 chirp mass 好测量吗？——对个别质量进行约束
当我们分析合并前的最后一圈运动时已经接受了两星体非常致密的结论，有人会问公式 7 在非牛顿体系下描述下正确吗。事实上对于最后一圈时部队的，在牛顿动力学稳定圆轨情况下可能存在很多种合并方式，而且能量流失到到引力波使得它们互相旋进（就是互相靠近吧？）。然而在广义相对论中，近到足够合并的物体（至少一个物体要远大于另一个）系统没有下文给出典型位置这样的轨道可以越过最内稳定圆轨（物体可以绕黑洞运行而不被黑洞吞噬的最近点）。允许的内部轨道只能是非圆轨和向心的（“plunge” inwards这儿我译的向心的）。因此在最后公转中轨道间距和频率的变化并不受引力波发射的公式7主导。这也就是为什么我们用峰值频率 $f_{GW}|_{max}$ 而不用最终频率 $f_{GW}|_{fin}$ 。

我们限制在 $f_{GW}|_{fin}$ 基础上约束各物体，因此我们后面就不需要牛顿近似了。至今还没有观测到超过 $3M_{\odot}$ 的中子星；我们将采取一个更保守的中子星质量上限值 $4.76M_{\odot}$ ，这是因为从早期可见周期信号中得到的 chirp mass 值（前面讨论的），为了让较小的那天体质量小于这个阈值（我想肯定是chirp mass），那么 $m_1$ 至少要 $476M_{\odot}$ ，也意味着质量比 $q\geq100$ 。我们的数据可能有这么高的质量比吗？这么高的质量比表明可以将系统视为极端质量比旋进系统，其中小质量轨道可以近似为沿着大质量的测地线轨道（ $m_1\sim \texttt{M}$ ，这个词在广相里说到过好像）。围绕物体附近的测试粒子的轨道频率与其质量成反比，包括无量纲自旋 $\chi$ 也是成反比。在半径为 r 的赤道轨道的无穷远圆轨测得的轨道频率 $w_{orb}$ （这里又是翻译不通）下式给出：

$w_{orb}=\frac{\sqrt{GM}}{r^{3/2}+\chi (\sqrt{GM}/c)^3}=\frac{c^3}{GM}(\chi+(\frac{c^2r}{GM})^{3/2})^{-1}$ (16)

举个例子，施瓦西半径黑洞的附近，四极矩引力波频率（这个名词以后改一下）在最内稳定圆轨道处（也就是在 $r=6GM/c^2$ ）因此等于 $f_{GW}=4.4(M_{\odot/M}) ~\texttt{kHz}$ ，然而对于极端 kerr 黑洞（ $\chi =1$ ）的最内稳定圆轨道（ $r=GM/c^2$ ）频率为 $w_{orb}=c^3/2GM$ ，且四极矩引力频率为 $f_{GW}=c^3/2\pi GM=32(M_{\odot/M}) ~\texttt{kHz}$ 。由于引力波迅速变弱，最高的期待频率接近于光环的频率（LR，哪儿冒出来的 light ring?!），因为没有任何物质的环绕能比光还快，并且当光环内的波在光环发出的位置遇到了有效势垒。光环位置在：

$r_{LR}=\frac{2GM}{c^2}(1+cos(\frac{2}{3})cos^{-1}(-x)))$ (17)

对于施瓦西黑洞的半径是 $3GM/c^2$ ，然而对于自旋黑洞而言随着自旋增加其光环半径在减小。对于极限黑洞其半径与最內圆稳定轨道半径一致都是 $GM/c^2$ 。则半径跌到 $m_1$ 时的最大引力波频率是67 Hz（最后这一句很不确定含义，到底是什么跌倒 m1 没看明白，从上下文一直在说半径，我就这么做了，太难了）。

由于我们测得的轨道发出的引力波比这个最大值要高很多，不管有没有自旋这个系统都不能用了（论文说的出局了）。因此呢即使质量要轻一点也至少要 $4.76M_{\odot}>3M_{\odot}$ ，比已知的中子星最大质量还大。

4.6 由光度的限制带来的可能红移

引力波在宇宙中传播时会因为宇宙膨胀而拉伸。相比于引力波刚发射出来的波长与频率，这种拉伸增加了波长和减小了频率。同样的效应也能解释光子从远处物体过来的红移现象。这对引力波的相位影响相当于在地球上测的质量的缩放比例（这个a scaling of the masses没有想明白）；公式 7 的无量纲分析表明源系下质量要比探测器系要小 $(1+z)$ 倍，其中 z 是红移量。探测器直接测量会产生受红移波影响的质量值。那么如何把它们从源值中区分出来?下一小节我们就估计离源的距离，因此嘞通过关联引力波振幅与光度从探测的合并产生的应力及流的信号，这样也可以估计红移。结果就是发现红移 $z \leq 0.1$ 所以探测器系或者源系下质量区别就小于10%的量级。

5 光度与距离

在物理讨论基础上也给了对引力波峰值处光度的估计，其离我们的距离和引力波辐射的总能量也估计了。

引力波的振幅 $h$ 随着光度距离 $d_L$ 增加而衰减的反比关系 $h\propto 1/d_L$ 。这些图一也说了，测量的应变峰值在 $h|_{max}\sim10^{-21}$ 。如果探测器离源再近十倍，那么测得的应变也会大十倍。这个反比关系在 $h$ 到达单位之前都是成立的，因为在靠近系统的施瓦西半径 $R\sim200~km$ 附近时引力的非线性将会很明显。这样我们就得到了一个离源距离的粗略的数量级上限：

$d_L<10^{21}\times 200km\sim6Gpc$ (18)

我们其实可以根据光度得到更精确的距离估计，因为从等质量双星系统的引力波光度有一个与质量无关的峰值。这是可以从四极矩公式的量纲分析看出来的，公式给了光度 $L\sim\frac{G}{c^5}M^2r^4w^6$ ，对于最后那几圈很紧密的公转有 $w\simc/r,r\sim GM/c^2,Mw\sim c^2/G$ 。将这些估计结合到普朗克光度公式：

$L\sim L_{Planck}=c^5/G=3.6\times10^{52}W$ (19)

然而仔细看公式（在附录A里的A4）的话发现给出的前面因子应该是 $\frac{32}{5}(\frac{\mu}{M})^2$ ，这样给出了等质量系统值为 $\frac{2}{5}$ 还很接近于 $q\sim 1$ 的情况。对于小质量物体掉入施瓦西半径的分析表明 $M\sim \frac{1}{6}c^2 r_{ISCO}/G,wr\sim0.5c$ 。将这些正确的指数参数结合起来，光度就要求有个因子 $0.4\times6^{-2}\times0.5^6\sim 0.2\times10^{-3}$ 。然而数值解可能因为一点自旋因子而发生变化，对质量接近的双星系统，我们可以将其数量级视为通用来用。

用公式 5 我们将引力波光度于其在光学距离 $d_L$ 处的应变值 $h$ 联系起来：

$L\sim\frac{c^3}{4}\frac{d^2_L}{G}|\dot{h}|^2\sim\frac{c^5}{4G}(\frac{w_{GW}d_Lh}{c})^2$ (20)

因此呢我们有：

$\frac{L_{peak}}{L_{Planck}}\equiv \frac{L|_{max}}{L_{Planck}}\sim0.2\times10^{-3}\sim(\frac{w_{GW}d_Lh|_{max}}{c})^2$ (21)

由此我们可以在整个周期下的振幅峰值处的测量的应变值中估计出距离：

$d_L\sim45Gpc(\frac{Hz}{f_{GW}|_{max}})(\frac{10^{-21}}{h|_{max}})$ (22)

对于GW信号得到距离 $d_L\sim300Mpc$ 。该距离对应于红移值 $z\leq 0.1$ ，因此基本上不会影响结论。对于依赖应变数据的其他距离光度计算方法看论文（达到的估计值都差不多）:L. M. Burko, arXiv:1602.04666 [physics.ed-ph] (2016)。

利用轨道能量 $E_{orb}$ (附录A中有定义)我们可以估计引力波在轨道间距非常远（以至于 $E_{orb}^i\rightarrow0$ ）到轨道间距为 r 时发出的系统总能量辐射。对于GW信号，利用估计 $m_1\sim m_2\sim35M_{\odot}$ 和 $r\sim R=350km$ ，得到：

$E_{GW}=E_{orb}^i-E_{orb}^f=0-(-\frac{GM\mu}{2R})\sim 3M_{\odot}3c^2$ (23)

这个值应当作为总能量辐射的下限估计（因为合并或者振荡时会放出能量），与1-3计算的精确结果相比而言的。

我们发现这次合并的大部分能量都很清楚。在其一千万年时间里，我们的太阳将不到1%的质量转化成了光和辐射。GW不仅释放了300倍引力波能量的能量（几乎完全超过了图1所展示那），而且对于一个周期内光度峰值，其以引力波形式释放的强度 $L_{peak}$ 大约比我们的太阳释放的强度的22个数量级。

6 结论

通过这些对GW观测的应变数据的物理性质讨论可以获得很多认识。这说明产生的引力波是由一对合并前彼此靠的很近的黑洞激发的。系统最后稳定下来极有可能时形成了一个黑洞。简单的讨论也能获得关于距离和其他的基本性质信息。

这些讨论后我们只得出关于质量比的有限结论，因为频率演化并不依赖于质量比。而质量比出现在后牛顿近似中，所以质量比值可以从数据中来得到更多的约束。

这些结论并不适用于所有信号，比如质量比如果特别低到一个中子星能被排除掉，就像小节 4.5 所做的。但至少对像GW这样的信号是管用的。已经有了另一个引力波探测了GW151226，其振幅要小一点，因此如果不用更先进的技术就没法在应变数据中看到。

这些技术结合了分析法和数值算法后能够给我们足够的信息。所以我鼓励读者们去探索这些算法与模型是如何用到估计这类系统的参数，并用来测试和限制高等相对论下广义相对论的结果，以及了解如何用到动力学和基于这个事件的天体物理的研究中。

在引力波观测的开始的时代，我们希望这篇论文作为进入这个领域的一个邀请作用。

附录A:双星系统的引力辐射计算

这里我们大概说一下双星系统引力波放出的能量和这些能量对系统的影响。

首先我们计算系统质量的四极矩 $Q_{ij}$ 。用笛卡尔坐标系 $\small X=(x_1,x_2,x_3)=(x,y,z)$ 其远点在质量中心，r 为距离原点的距离。 $\small \delta _{ij}=\texttt{diag}(1,1,1)$ 是Kronecker符号， $\small \rho(x)$ 代表质量密度。故：

$\small Q_{ij}=\int d^3x \rho(X)(x_ix_j-\frac{1}{3}r^2\delta_{ij})$ (A1)

$\small =\sum_{A\in \{1,2\}}m_A(\begin{array}{ccc} \frac{2}{3}x^2_A-\frac{1}{3}y^2_A & x_Ay_A& 0\\ x_Ay_A& \frac{2}{3}y^2_A-\frac{1}{3}x^2_A &0\\ 0 &0&-\frac{1}{3}r^2_A \end{array} )$ (A2)

其中第二等式在双星系统在xy平面上才成立。对于简单的圆轨情况，距离 $\small r=r_1+r_2$ 频率则为 $\small f=\frac{w}{2\pi}$ ，对每个对象用三角形分析如图A1：

$\small Q_{ij}^A(t)=\frac{m_Ar_A^2}{2}I_{ij}$ (A3)

其中 $\small I_{xx}=cos(2wt)+\frac{1}{3},I_{yy}=\frac{1}{3}-cos(2wt),I_{xy}=I_{yx}=sin(2wt),I_{zz}=-\frac{2}{3}$ 。结合起来就得到 $\small Q_{ij}(t)=\frac{1}{2}\mu r^2I_{ij}$ ，从公式5得到的引力波光度是：

$\small \frac{d}{dt}E_{GW}=\frac{32}{5}\frac{G}{c^5}\mu^2r^4w^6$ (A4)

能量的这种流失会消耗轨道能量 $\small E_{orb}=-\frac{GM\mu}{2r}$ ，因此呢 $\small \frac{d}{dt}E_{orb}=\frac{GM\mu}{2r^2}\dot{\mathbf{r}}=-\frac{d}{dt}E_{GW}$ 。为了可以用开普勒定律去近似轨道，我们假设辐射到各轨道的能量要远小于轨道能量

接下来用开普勒第三定律 $\small r^3=GM/w^2$ 而且其导数 $\small \dot{\mathbf{r}}=-\frac{2}{3}r\dot{w}/w$ 我们就能把所有的 r 值替换掉，然后得到：

$\small \dot{w}^3=(\frac{96}{5})^3\frac{w^{11}}{c^{15}}G^5\mu^3M^2=(\frac{96}{5})^3\frac{w^{11}}{c^{15}}(G~\texttt{M})^5$ (A5)

已经定义的 chirp mass $\small \texttt{M}=(\mu^3M^2)^{1/5}$ 。

我们可以发现，在开普勒定律导致轨道间距缩小时，公式 A5 描述了系统的激发演化过程。

A.1 不同旋转系统的引力辐射

在其它旋转系统中，引力波振幅会随着频率增加而增加。频率以增加系统就会越转越快，除非获得角动量，否则系统的尺寸长度 $\small r(t)$ 就会减少。对于不受能量损失影响和引力波角动量影响的系统，也很难一下损失很多角动量，因此系统会保持其角动量 $\small L=\alpha Mr^2w$ ，所以就有 $\small w\propto L/r^2$ 。

四极矩公式 4 也说明引力波应变应振幅应符合四极矩的二阶时间导数， $\small h\propto Mr^2w^2\propto Lw$ 。

因此我们知道对于不受引力波发射影响的系统，当其系统尺寸 $\small r$ 明显缩小时其引力波频率与振幅都会增加，但是仍然彼此保持一定比例。但是这与GW的数据是不一致的，图二说明振幅增长2倍时候而频率至少增加了5倍。

附录B：特大和致密星体的可能性

我们考虑质量范围在 $\small m\sim35M_{\odot}$ 的天体被约束到半径为 R 从而致密率满足 $\small \mathfrak{R}=\frac{c^2R}{Gm}\lesssim3.4$ 。这导致了牛顿密度有了范围值：

$\small \rho\geq \frac{m}{(4\pi/3)R^3}=3\times10^{15}(\frac{3.4}{\mathfrak{R}})^3(\frac{35M_{\odot}}{m})^2\frac{kg}{m^3}$ (B1)

其中等式对于成分一致的物体才成立。这个密度要比白矮星高 $\small 10^6$ 倍，因此我们可以排除它是其他主序星那样靠电子简并压支持情况。然而这个密度比中子星密度要少大约 $\small 10^2$ 个量级，中子星质量极限大概 $\small 3M_{\odot}$ ，这些星体质量超过了最大的中子星质量一个数量级。对于频率变化的更细致分析包括潮汐扭力影响必然要求更加致密以满足最后一次公转的轨频率。这将使得大家伙越发逼近中子星密度，因此将状态方程约束到一个跟紧密的地步。尽管理论上对于均匀物质的致密率低到 $\small \mathfrak{R}=4/3$ 是合理的，我们会得到数据确实说明如果这些物体有一个是物质构成的，它就需要在恒星到处都有的环境下中占据一个极端、狭窄且迄今为止从未探索与观测到的位置。有这样致密性和质量的最像的物体就是黑洞了。

附录C：后激发相位：我们能从振荡和最终物体得到什么结论？

待完成

妖歌长安

关注

3
点赞
踩
5

收藏

觉得还不错? 一键收藏
0
评论
论文翻译：The basic physics of the binary black hole merger GW150914（引力波发现的那双黑洞的基本物理性质，2016.10.4发表）

摘要：2015年9月14日，LIGO第一次探测到了GW（一个恒星级双黑洞）的引力波信号，给爱因斯坦广义相对论预言强有力的证明。信号被LIGO两个探测器（LA和WA，简写）探测到。而提取关于源的全部信息需要更深入的分析方法和计算机算法。然而，对于普通人来讲可以从这次直接观测中知道更多。这个简单的分析表明信号源时两个互相绕转的黑洞并且合并形成了另一个黑洞。黑洞是时空的奇点其引力场强到以至于没有任何...
复制链接

扫一扫