PyTorch 量化 原理与复现

   神经网络的量化是指将浮点数的权重和（或）activation用定点数表示，此外，比较完全的量化还希望整个网络的数学运算全部是基于定点数的数学运算。对于定点数来讲，小数点的选取是人为的，（例如一个3比特的定点数的二进制形式为101，如果我们把小数点定在第一位之前，这个数就表示0.625；如果把小数点放在最后一位之后，就表示5）因此也往往称定点数量化为整数量化。
   深度神经网络的量化方法有很多，但目前工业界的主流是INT8量化，即量化位宽为8比特 [1]。个人总结认为选用8比特位宽的主要原因有两个：

• 一是为了适应与CPU、GPU等较为通用的硬件平台
• 二是8比特的位宽在实验中被证实对于目前最流行的网络（例如MobileNet等）不会导致明显精度下降

对于第一点，当然如果硬件平台是更底层的FPGA或者ASIC，可以考虑低于8比特的更不规则的量化位宽。
   神经网络的量化最主要的作用有3个方面：一是压缩模型大小的；二是加速模型推理（我了解的量化还是对于推理阶段，训练阶段好像都是用浮点计算保证精度）；三是量化后的模型能更高效地进行硬件（例如ASIC）实现。naive的量化大概率会引起模型精度下降（但是好像对于MNIST数据集的模型精度下降也不明显，主要是大规模的网络），因此需要精心设计量化方案。在Google退出量化感知训练之后，量化可以以是否重训练为划分标准分为：无训练量化和有重训练的量化。

• 无训练量化是指在拿到已经训练好的浮点数模型之后，整个量化过程不会再进行训练（但可能会有推理）
• 有重训练量化指的是在对已经训练好的浮点数模型进行量化的过程中，会需要重训练

1 量化方案

   我们首先介绍INT8量化的量化方案，TensorFlow和PyTorch的量化实现均是基于这个量化方案。其中NVIDIA的量化方案公开得更早一点，但仅仅是无训练量化的方案；Google的量化方案公开得稍晚，首次公开是通过论文 [3]，其中包括了含有重训练的量化方法。

1.1 NVIDIA方案

   NVIDIA的量化方案在 [4] 中的PDF给出。在网上很多博客有详细的解释。因为Google的量化方案包含了NVIDIA的方案并且更加完善，提供的资料也更多，因此我们粗略地讲解NVIDIA的量化方案，然后将部分内容放到Google的方案中一起讲解。
   一个浮点数到int8定点数的量化关系可以表示为
$$r=s\times q+b.$$其中$r$,$s$,$b$是浮点数，$q$是int8定点数。$s$是把定点数映射到浮点数上的scaling factor，$b$是bias。NIVIDIA的实验表明，$b$可以去掉而没有明显精度损失。因此，在NIVIDA给出的方案中，浮点数与int8定点数之间就是纯粹的按比例映射：
$$r=s\times q.$$

1.2 Google方案

1.2.1 浮点数-定点数映射

   Google的量化方案保留了bias，但是他给bias的赋予了新的解释，称之为zero-point（零点）。仍然是利用线性映射，浮点数$r$和int8定点数$q$之间的关系表示为：
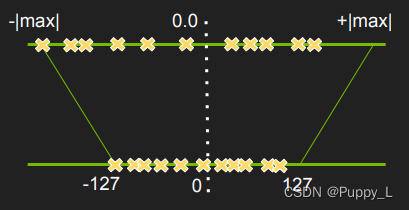
$$r=S(q-Z).$$其中$S$是scaling factor，是一个浮点数；$Z$是零点，是一个定点数。$Z$代表的是浮点数的0映射到定点数上的值。这里借用NVIDIA pdf中的一个图来说明浮点到定点的映射，图中浮点的0的位置对应定点的0，这是因为这个图里面浮点数的表示范围正负对称了（虽然图里面看起来好像正负并不对称，因为正轴上的叉代表的最大绝对值明显更小，但是图里面用的max是一样的）。

   为求得scaling factor，我们需要知道$r$的最大值与最小值，分别记为$r_{max}$和$r_{min}$。同样地，$q$也有最大值与最小值，记为$q_{max}$和$q_{min}$。$q$的位宽虽然是8比特，但是可能是有符号形式或者无符号形式，因此取值范围不同。对于无符号形式，取值范围为
$[q_{min},q_{max}]=[0,255]$；无符号形式有$[q_{min},q_{max}]=[-128,127]$。注意取值可以人为进行规定，例如在TensorFlow的TensorFlow Lite 8 位量化规范中 [5]，权重的取值范围为$[-127,127]$，而activation的取值范围为$[-128,127]$。至此，我们给出scaling factor $S$的计算方式：
$$S=\frac{r_{max}-r_{min}}{q_{max}-q_{min}}.$$零点计算方法为
$$Z=⟨q_{max}-\frac{r_{max}}{S}⟩.$$其中$⟨\cdot ⟩$是四舍五入取整。

例如我们有$[r_{min},r_{max}]=[-1,1]$和$[q_{min},q_{max}]=[-127,127]$，则
$$S=\frac{1-(-1)}{127-(-127)}=\frac{2}{254}.$$这个映射显然两个范围完全，因此我们猜想零点也是0。计算零点
$$Z=⟨127-\frac{1}{\frac{2}{254}}⟩=0.$$
   在看一个浮点数范围与定点数不对称的例子。假设有$[r_{min},r_{max}]=[-1,1]$和$[q_{min},q_{max}]=[0,255]$，
$$S=\frac{1-(-1)}{255-0}=\frac{2}{255}.$$$$Z=⟨255-\frac{1}{\frac{2}{255}}⟩=127.$$

1.2.2 定点数算数运算

两个数的乘法
   仅仅是量化权重和activation是不够的，为了进一步加速推理，并且利于高效硬件实现，我们需要将所有的运算全部在定点数上进行。这一节我们说明如何将神经网络的乘加运算放到定点数上。
   首先考虑最简单的两个数的乘法，记$r_1$和$r_2$相乘得到$r_3$，即
$$r_1\times r_2=r_3,$$三者均是浮点数。
写成定点数的形式为
$$S_1(q_1-Z_1)S_2(q_2-Z_2)=S_3(q_3-Z_3).$$简单变换可以得到
$$q_3=\frac{S_1{S}_2}{S_3}(q_1-Z_1)(q_2-Z_2)+Z_3.$$其中只有$\frac{S_1{S}_2}{S_3}$是浮点数。在[3]中表示实验发现$\frac{S_1{S}_2}{S_3}$总是在$(0,1)$之间，于是将他表示成
$$\frac{S_1{S}_2}{S_3}=2^{-n}{M}_0,$$$M_0$是一个$[0.5,1)$上的数，$n$是一个非负数。假如用int32，即32位的整数来表示$M_0$，则[3]给出表示方法为
$$\frac{S_1{S}_2}{S_3}=2^{-31}{M}_0.$$$M_0$用int32表示，且小数点在第1位之前。假设二进制形式下$M_0=1011$，则他表示的是$0.1011$，等于0.6875。[3]中说$M_0$的取值范围为$[0.5,1)$，但是我没有太清楚为什么。总之，综上我们可以看出，$\frac{S_1{S}_2}{S_3}$是一个$(0,1)$之间的小数，并且用63位定点数表示（$M_0$是32位定点数，$2_{-31}$对应移位31）。并且，这种表示方式表明$\frac{S_1{S}_2}{S_3}$的二进制定点表示数的最高的31位均是零，而低32位是$M_0$。我们记$M_0$的二进制表示为
$$0.\underset{32比特}{\underbrace{M_{0,1},M_{0,1},\cdots ,M_{0,32}}}.$$则$\frac{S_1{S}_2}{S_3}$被表示为
$$0.\underset{31个0比特}{\underbrace{00\cdots 0}}\underset{32比特}{\underbrace{M_{0,1},M_{0,1},\cdots ,M_{0,32}}}.$$这里其实有点疑问，就是如果$\frac{S_1{S}_2}{S_3}$可以表示成这么小的一个值（前31位都是0），那么意味着$S_3$要比$S_1{S}_2$大很多，差不多31个数量级，但这是不对的。$S_3$对应多个int8的输入与int8的权重的乘累加，即使是上千个输入累加，最大表示的范围也就变为$2^8\times 2^8\times 2^{10}=2^{26}$，位宽为26。这里虽然是粗略估计，但是$S_3$显然不可能数值上大$S_1\times S_2$ 31个数量级。

乘累加以及bias
   后面讨论PyTorch的量化方法的时候，我们会详细讨论基于tensor和基于channel的两种量化方案，基于channel的量化方案是更细粒度的量化，他保证了一个tensor的每个channel上的scaling factor S以及零点Z是一样的。这意味着一个神经元的乘累加运算中，所有输入的S和Z相同。考虑一个有$N$个输入的神经元的乘累加为
$$r_3=\sum _{i=1}^N{r}_{1,i}\times r_{2,i}.$$$r_{1,i}$是输入的activation，他们拥有相同的$S_1$和$Z_1$；$r_{2,i}$是对应权重，他们拥有相同的$S_2$和$Z_2$。写成量化形式并变换得到
$$\begin{array}{rl}{q}_3& =\frac{S_1{S}_2}{S_3}\sum _{i=1}^N(q_{1,i}-Z_1)(q_{2,i}-Z_2)+Z_3\\ & =2^{-n}{M}_0\sum _{i=1}^N(q_{1,i}-Z_1)(q_{2,i}-Z_2)+Z_3\end{array}.$$在[3]中还将括号展开进一步化简，我们这里就不进一步讨论了。
   考虑有bias的情况，
$$r_3=\sum _{i=1}^N{r}_{1,i}\times r_{2,i}+b.$$量化形式为
$$\begin{array}{rl}{q}_3& =\frac{S_1{S}_2}{S_3}\sum _{i=1}^N(q_{1,i}-Z_1)(q_{2,i}-Z_2)+\frac{b}{S_3}+Z_3\\ & =\frac{S_1{S}_2}{S_3}[\sum _{i=1}^N(q_{1,i}-Z_1)(q_{2,i}-Z_2)+b_Q]+Z_3\\ & =2^{-n}{M}_0[\sum _{i=1}^N(q_{1,i}-Z_1)(q_{2,i}-Z_2)+b_Q]+Z_3\end{array}.$$其中$b=\frac{S_1{S}_2}{S_3}{b}_Q$，$b_Q$是int32比特量化的bias，并且零点为0.

   上面的式子涉及到两个int8整数的乘法，显然乘积应该用16比特表示。但又因为有求和，多个16比特整数可能有更大的数值，需要更大位宽表示。同时考虑到$b_Q$是用int32表示的，因此上面的乘累加的中间值均用int32表示，即用int32的精度计算${\sum }_{i=1}^N(q_{1,i}-Z_1)(q_{2,i}-Z_2)+b_Q$。在https://github.com/tensorflow/tensorflow/blob/4952f981be07b8bf508f8226f83c10cdafa3f0c4/tensorflow/contrib/lite/kernels/internal/reference/reference_ops.h#L493-L534中的493到534行给了全连接的实现代码。

可以看到乘累加中间过程精度均为int32。其中的MultiplyByQuantizedMultiplierSmallerThanOne则是实现与$2^{-n}{M}_0$的乘法，如下图所示

其中SaturatingRoundingDoublingHighMul是用于实现与$M_0$的乘法，中间过程用更高的int64精度，最后只保留高32位，因此与$M_0$的乘积还是采用的int32。但是最后对应$2^{-31}$的31位位移应该会将这个int32位的数变成最大值小于1的数，而不是int8。这里没太弄懂怎么转换回int8的。

加法以及concatenate
   在ResNet等一些模型中，存在单纯的加法（不是不是乘累加中的加法）和concatenation，因此也需要考虑如何进行量化形式的变换。这个部分还没有完全弄懂，可以参考[2]以及[6]。

1.3 PyTorch量化实现

   PyTorch的量化和TensorFlow基本一直，但PyTorch的量化API退出更晚，也更不完善。可是鉴于PyTorch的使用率逐渐提高，应该也没有人会为了量化方便而又去学用TensorFlow吧，希望PyTorch的量化方案以后更完善一点。。。
   PyTorch的量化分为3大类 [2] [7]：

• Dynamic quantization 动态量化
• Static quantization 静态量化
• Quantization aware training 量化感知训练

其中动态量化是对权重进行线下量化，即拿到训练好的浮点模型后量化权重。但是对于activation，是根据推理过程中activation的取值范围进行量化，这意味着同一个模型在处理不同输入图片时，activation采用的量化参数很可能是不一样的。动态量化其实并不是最优方案，毕竟运算过程中量化是很少见的实现方式，因此对应于动态量化，静态量化是在拿到训练好的浮点模型后，对权重和activation均进行线下量化。因此同一个量化模型在处理不同图片时的量化参数是一样的。量化感知训练是通过量化后的重训练改善量化模型的精度，对于某些（例如MobileNet）在静态量化下精度损失较大的网络有着明显精度提升。
   因为动态量化很少用到，我们只关注静态量化和量化感知训练。

1.3.1 静态量化

   首先，静态量化可以基于tensor和基于channel。在PyTorch和TensorFlow中，向量基本计算单元均是tensor，他的维度是4维：输出channel数目，输入channel数目，高度，宽度。对于卷积来说，一个filter包含多个卷积核，每个卷积核（kernel）对应一个输出channel，高度和宽度则是卷积核的高度和宽度。对于一个activation向量，输入channel数目为1，维度降低到3维。基于tensor的量化中，每个tensor使用的S和Z是一样的；而在基于channel的量化中，每个channel的权重或者每个channel的activation是一样的。
   在PyTorch中，静态量化分为两大类：最简单的是基于tensor的量化，并且采用真实的$r_{max}$, $r_{min}$, $q_{max}$和$q_{min}$；第二类是基于channel的量化，采用KL散度（相对熵）来衡量量化的好坏，并选取使得相对熵最小的阈值来做饱和量化。目前PyTorch量化的模型只支持CPU的计算。

1.3.1.1 一些准备和注意事项

   在PyTorch的官网上给出了详细的教程 [9]，此教程以MobileNetV2为例。在PyTorch的nn.Modules中有写好的浮点数MobileNetV2的网络结构，可以直接调用，但是为例做量化，需要对网络结果进行手动修改，主要包括：

• 量化与反量化模块的添加：QuantStub()，DeQuantStub()
• 加法以及concatenate单元的量化替换
• 模块融合

因此，在[9]中直接给出了MobilNetV2的量化模型的代码，可以复制粘贴调用。对于一个量化网络的forward函数，需要在输入时用QuantStub()将输入的tensor转换为量化的类型，并且在输出时用DeQuantStub()将量化类型的tensor转换回普通类型。注意量化类型的tensor可支持的算子没有普通类型的丰富，因此如果将量化类型的tensor传入某些不支持的算子就会报错。下面是[9]中给出的用于量化的MobileNetV2模型。

from torch.quantization import QuantStub, DeQuantStub

def _make_divisible(v, divisor, min_value=None):
    """
    This function is taken from the original tf repo.
    It ensures that all layers have a channel number that is divisible by 8
    It can be seen here:
    https://github.com/tensorflow/models/blob/master/research/slim/nets/mobilenet/mobilenet.py
    :param v:
    :param divisor:
    :param min_value:
    :return:
    """
    if min_value is None:
        min_value = divisor
    new_v = max(min_value, int(v + divisor / 2) // divisor * divisor)
    # Make sure that round down does not go down by more than 10%.
    if new_v < 0.9 * v:
        new_v += divisor
    return new_v


class ConvBNReLU(nn.Sequential):
    def __init__(self, in_planes, out_planes, kernel_size=3, stride=1, groups=1):
        padding = (kernel_size - 1) // 2
        super(ConvBNReLU, self).__init__(
            nn.Conv2d(in_planes, out_planes, kernel_size, stride, padding, groups=groups, bias=False),
            nn.BatchNorm2d(out_planes, momentum=0.1),
            # Replace with ReLU
            nn.ReLU(inplace=False)
        )


class InvertedResidual(nn.Module):
    def __init__(self, inp, oup, stride, expand_ratio):
        super(InvertedResidual, self).__init__()
        self.stride = stride
        assert stride in [1, 2]

        hidden_dim = int(round(inp * expand_ratio))
        self.use_res_connect = self.stride == 1 and inp == oup

        layers = []
        if expand_ratio != 1:
            # pw
            layers.append(ConvBNReLU(inp, hidden_dim, kernel_size=1))
        layers.extend([
            # dw
            ConvBNReLU(hidden_dim, hidden_dim, stride=stride, groups=hidden_dim),
            # pw-linear
            nn.Conv2d(hidden_dim, oup, 1, 1, 0, bias=False),
            nn.BatchNorm2d(oup, momentum=0.1),
        ])
        self.conv = nn.Sequential(*layers)
        # Replace torch.add with floatfunctional
        self.skip_add = nn.quantized.FloatFunctional()

    def forward(self, x):
        if self.use_res_connect:
            return self.skip_add.add(x, self.conv(x))
        else:
            return self.conv(x)


class MobileNetV2(nn.Module):
    def __init__(self, num_classes=1000, width_mult=1.0, inverted_residual_setting=None, round_nearest=8):
        """
        MobileNet V2 main class
        Args:
            num_classes (int): Number of classes
            width_mult (float): Width multiplier - adjusts number of channels in each layer by this amount
            inverted_residual_setting: Network structure
            round_nearest (int): Round the number of channels in each layer to be a multiple of this number
            Set to 1 to turn off rounding
        """
        super(MobileNetV2, self).__init__()
        block = InvertedResidual
        input_channel = 32
        last_channel = 1280

        if inverted_residual_setting is None:
            inverted_residual_setting = [
                # t, c, n, s
                [1, 16, 1, 1],
                [6, 24, 2, 2],
                [6, 32, 3, 2],
                [6, 64, 4, 2],
                [6, 96, 3, 1],
                [6, 160, 3, 2],
                [6, 320, 1, 1],
            ]

        # only check the first element, assuming user knows t,c,n,s are required
        if len(inverted_residual_setting) == 0 or len(inverted_residual_setting[0]) != 4:
            raise ValueError("inverted_residual_setting should be non-empty "
                             "or a 4-element list, got {}".format(inverted_residual_setting))

        # building first layer
        input_channel = _make_divisible(input_channel * width_mult, round_nearest)
        self.last_channel = _make_divisible(last_channel * max(1.0, width_mult), round_nearest)
        features = [ConvBNReLU(3, input_channel, stride=2)]
        # building inverted residual blocks
        for t, c, n, s in inverted_residual_setting:
            output_channel = _make_divisible(c * width_mult, round_nearest)
            for i in range(n):
                stride = s if i == 0 else 1
                features.append(block(input_channel, output_channel, stride, expand_ratio=t))
                input_channel = output_channel
        # building last several layers
        features.append(ConvBNReLU(input_channel, self.last_channel, kernel_size=1))
        # make it nn.Sequential
        self.features = nn.Sequential(*features)
        self.quant = QuantStub()
        self.dequant = DeQuantStub()
        # building classifier
        self.classifier = nn.Sequential(
            nn.Dropout(0.2),
            nn.Linear(self.last_channel, num_classes),
        )

        # weight initialization
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                nn.init.kaiming_normal_(m.weight, mode='fan_out')
                if m.bias is not None:
                    nn.init.zeros_(m.bias)
            elif isinstance(m, nn.BatchNorm2d):
                nn.init.ones_(m.weight)
                nn.init.zeros_(m.bias)
            elif isinstance(m, nn.Linear):
                nn.init.normal_(m.weight, 0, 0.01)
                nn.init.zeros_(m.bias)

    def forward(self, x):

        x = self.quant(x)

        x = self.features(x)
        x = x.mean([2, 3])
        x = self.classifier(x)
        x = self.dequant(x)
        return x

    # Fuse Conv+BN and Conv+BN+Relu modules prior to quantization
    # This operation does not change the numerics
    def fuse_model(self):
        for m in self.modules():
            if type(m) == ConvBNReLU:
                torch.quantization.fuse_modules(m, ['0', '1', '2'], inplace=True)
            if type(m) == InvertedResidual:
                for idx in range(len(m.conv)):
                    if type(m.conv[idx]) == nn.Conv2d:
                        torch.quantization.fuse_modules(m.conv, [str(idx), str(idx + 1)], inplace=True)

   而非量化版本的模型在https://github.com/pytorch/vision/blob/main/torchvision/models/mobilenetv2.py上给出，对比可以发现量化版本最主要的变化是：

• 在forward中添加了量化和反量化函数
• 将浮点模型的加法x + self.conv(x)替换为skip_add.add(x, self.conv(x))
• 将ReLU6替换为ReLU

这些变化更详细地说明参考[10]。上述的量化模型可以和浮点模型一样进行推理训练等等。
   值得注意的是，虽然[9]单独贴出了MobilNetV2的模型代码，但实际上PyTorch在vision/torchvision/models/quantization/mobilenetv2.py 中已经给出了相关的代码，可以直接调用：

from torchvision.models import quantization
model = quantization.mobilenet_v2()

1.3.1.2 模块融合

   batch-normalization（BN）作为一种线性变换，当紧跟在全连接或者卷积后面的时候，是可以与他们融合的，即使是非量化的网络，在结束训练只考虑推理的时候，融合BN也是提升推理速度提高效率的有效方式。BN的原理如下图，其中$\gamma$和$\beta$是可学习的参数，在训练结束后确定；${\mu }_B$和${\sigma }_B$分别是输入$x_i$的平均值和标准差，在训练的过程中通过对所有$x_i$进行统计得到；$ϵ$是一个非零极小值，为了保证分母不为0。BN层主要是为了加快收敛。

   在训练结束后，BN层实际上就是为了实现下列的线性变换：
$$y_i=\frac{\gamma }{\sqrt{{\sigma }_B^2+ϵ}}{x}_i+(\beta -\frac{\gamma {\mu }_B}{\sqrt{{\sigma }_B^2+ϵ}})$$因此，与卷积或者全连接融合后，权重$w$变为
$$w\times \frac{\gamma }{\sqrt{{\sigma }_B^2+ϵ}}$$偏置$b$变为
$$b\times \frac{\gamma }{\sqrt{{\sigma }_B^2+ϵ}}+(\beta -\frac{\gamma {\mu }_B}{\sqrt{{\sigma }_B^2+ϵ}})$$
   卷积与BN融合的代码实现可以参考[11]，我复现了，测试了一两个网络，有明显的处理速度的提升。但是在PyTorch量化中，不要用自己的融合模块，将会出错，后面将说明出错点。

1.3.1.3 基于tensor的最简单量化

   [9]中提供了URL来下载训练好的MobileNetV2的参数，但是我没太弄懂怎么搞。。。所以我的实现中先加载一个PyTorch提供的预训练的MobileNetV2网络，然后把他的参数存下来。再加载量化的MobileNetV2，把存好的参数读进去。

# load the pretrained MobileNeytV2 and extract its parameters
model = models.mobilenet_v2(pretrained=True)
torch.save(model.state_dict(), 'saved_model/model_mobilenet_v2_state_dict.pth')

# instantiate the quantized model and load the saved parameters
#model = quantization.mobilenet_v2(pretrained=True) 
model = my_model.MobileNetV2()
model.load_state_dict(torch.load('saved_model/model_mobilenet_v2_state_dict.pth'))

这里的my_model保存了[9]中MobileNetV2的代码，也可以用

model = quantization.mobilenet_v2(pretrained=True) 

直接调用PyTorch内置的模型，基本上是一样的。
   通过以上方式，我对初始化的模型进行推理，精度有71.8%几，四舍五入到71.9%，和官网一致，但实际上我对比过浮点数的MobileNetV2的精度，以及我们使用的预加载该浮点数MobileNetV2的参数的量化的MobileNetV2，发现后者的精度稍差一点点，大概就是低万分之几。我个人认为是因为量化模型中把浮点模型中的ReLU6替换成了ReLU，导致了精度的不完全一致。
   将batch size和[9]中一样定为50，测试融合前后处理20个batch的速度分别为16s和11s，可见融合BN对速度还是有很大的提升。并且PyTorch的融合函数在卷积、BN、ReLU三者连着的时候不仅只融合卷积核BN，而是将3者融合在一起。观察融合前后的MobileNetV2第一层（第一层是普通的卷积层，参考论文《MobileNetV2: Inverted Residuals and Linear Bottlenecks》Tabel2）的网络结构。

   一定要注意的是，融合前一定要调用model.eval()。eval()本来是用来在推理阶段终止dropout和正则化等训练时更新的网络参数的，刚开始我认为融合这个过程也不会涉及到网络参数的更新，即使更新了也不影响我们量化，因为毕竟权重偏置啥的也不会再更新了。可是事实上是，融合前一定要调用model.eval()，否则最后量化的结果将是错误的。

# fuse some submodules of the model
print('\n Inverted Residual Block: Before fusion\n\n',model.features[1].conv)
model.eval()
model.fuse_model()
#model_fuse.fuse_module(model)
print('\n Inverted Residual Block: After fusion\n\n',model.features[1].conv)

   最后得到的精度是55.90%，和官方给出的56.7%并没有完全对上，不知道问题在哪。。。模型大小从原来的14.26M，到融合后的13.99M，再到量化后的3.63M。推理速度也有了明显提升。

1.3.1.4 基于channel的量化

   仍然是上面的网络，按照[9]中的代码执行，但是calibration这一步采用所有batch（[9]中只用了32个batch），最后的精度结果是67.23%，离官方给的67.3%的精度还是差一点点。但是完全按照官方给的batch size为50，校准32个batch的方案得到的精度只有64.66%，不知道为啥我总是比官方的结果差一点点。。。

1.3.1.5 基于tensor和基于channel的量化原理

   基于tensor的最简单的量化另每个tensor使用相同$S$和$Z$。在1.2中我们知道
$$S=\frac{r_{max}-r_{min}}{q_{max}-q_{min}}.$$
$$Z=⟨q_{max}-\frac{r_{max}}{S}⟩.$$$q_{max}$和$q_{min}$是人为确定的，并且权重的$r_{max}$和$r_{min}$是很好确定的（因为我们已经拿到了训练好的浮点模型参数）。因此我们在基于tensor量化的过程中，有一步校准（calibration）就是为了统计activation的$r_{max}$和$r_{min}$。在PyTorch中校准的实现就是进行多推理，在推理的过程中观察每层activation的最大值与最小值。因此在校准前的prepare就是在相应的地方插入observer，用以观察范围。显然，遍历所有图片得到的最大值最小值是最优的，但是实验表明其实只需统计部分的batch，得到的$r_{max}$和$r_{min}$用以量化就已经足够好。比如下面官方的代码里只观察了32个btach（每个batch50张图片）。

num_calibration_batches = 32

myModel = load_model(saved_model_dir + float_model_file).to('cpu')
myModel.eval()

# Fuse Conv, bn and relu
myModel.fuse_model()

# Specify quantization configuration
# Start with simple min/max range estimation and per-tensor quantization of weights
myModel.qconfig = torch.quantization.default_qconfig
print(myModel.qconfig)
torch.quantization.prepare(myModel, inplace=True)

# Calibrate first
print('Post Training Quantization Prepare: Inserting Observers')
print('\n Inverted Residual Block:After observer insertion \n\n', myModel.features[1].conv)

# Calibrate with the training set
evaluate(myModel, criterion, data_loader, neval_batches=num_calibration_batches)
print('Post Training Quantization: Calibration done')

# Convert to quantized model
torch.quantization.convert(myModel, inplace=True)
print('Post Training Quantization: Convert done')
print('\n Inverted Residual Block: After fusion and quantization, note fused modules: \n\n',myModel.features[1].conv)

print("Size of model after quantization")
print_size_of_model(myModel)

top1, top5 = evaluate(myModel, criterion, data_loader_test, neval_batches=num_eval_batches)
print('Evaluation accuracy on %d images, %2.2f'%(num_eval_batches * eval_batch_size, top1.avg))

有了$S$和$Z$，量化剩下的步骤就是把所有的$r$转化成$q$：
$$q=⟨\frac{r}{S}⟩+Z$$
有意思的是，当$r=r_{max}$时
$$q=⟨\frac{r_{max}}{\frac{r_{max}-r_{min}}{q_{max}-q_{min}}}⟩+⟨q_{max}-\frac{r_{max}}{\frac{r_{max}-r_{min}}{q_{max}-q_{min}}}⟩\approx q_{max}$$当$⟨q_{max}-\frac{r_{max}}{\frac{r_{max}-r_{min}}{q_{max}-q_{min}}}⟩$向上取整时,$⟨\frac{r_{max}}{\frac{r_{max}-r_{min}}{q_{max}-q_{min}}}⟩$向下取整；反之$⟨\frac{r_{max}}{\frac{r_{max}-r_{min}}{q_{max}-q_{min}}}⟩$向上取整。只有当$\frac{r_{max}}{\frac{r_{max}-r_{min}}{q_{max}-q_{min}}}=0.5$时两者均向上取整，相加结果会比$q_{max}$大1。
   基于channel的量化方法除了把参数$S$和$Z$的细粒度提升到channel级别，还对量化方案做了小修改。原本1.2的量化称之为非饱和量化，因为没有一个饱和值，量化范围反映了原浮点数的真实范围。实际上，在某些时候，较大的浮点数值也许没那么多；另一方面，模型中数值的相对大小才是真实反应其影响的量。相对大小的思想告诉我们，在量化中，我们如果把某些特别大的浮点数用足够大的定点数表示，也许就足够了，因为在定点数的系统中，这个被量化的数已经比其他的被量化的数大，保证了相对大小。基于上述讨论，引出一种称之为饱和量化的量化方案。考虑一个阈值$T>0$，当浮点数大于$T$时量化为$q_{max}$；小于$-T$时量化为$q_{min}$；在$T$和$-T$之间仍然z妇之前的线性量化方案。NVIDIA的实验表明对activation采用这种量化方案可以带来明显的精度提升效果。这种方案带来精度提升的一个直接原因是缩小了需要表示的浮点数的范围，使得可表示的浮点数更多了。

   因此，基于饱和量化的$S$和$Z$的计算公式变为
$$S=\frac{T-(-T)}{q_{max}-q_{min}}=\frac{2T}{q_{max}-q_{min}}.$$
$$Z=⟨q_{max}-\frac{T}{S}⟩.$$有了$S$和$Z$，$r$转化成$q$的公式为：
$$q=clamp(q_{min},q_{max},⟨\frac{r}{S}⟩+Z).$$其中$clamp(a,b,x)$是一个阶截断函数，他表示
$$clamp(a,b,x)=\{\begin{array}{l}b,\text{if}x>b\\ a,\text{if}x<a\\ x,\text{otherwise}\end{array}$$这是因为当$r=r_{max}$时
$$⟨\frac{r_{max}}{\frac{2T}{q_{max}-q_{min}}}⟩+⟨q_{max}-\frac{T}{\frac{2T}{q_{max}-q_{min}}}⟩$$是很可能大于$q_{max}$的（同理取最小值时也小于$q_{min}$），因此需要一个阶段函数保证量化后数值的正确性。
   现在的问题是如何确定阈值$T$？
   [4]中提出利用交叉熵（KL散度）来衡量量化编码与浮点编码两种对表示方式之间的差距，交叉熵越小表示量化编码越接近浮点编码。因此，找寻阈值的过程就是测试多种阈值并选择交叉熵最小的阈值的过程。更详细地讨论可见[8]，因为我也没弄懂细节o(╥﹏╥)o。

1.3.2 静态量化更多的实验结果

1.3.2.1 MNIST

   MNIST实际上是一很小的网络，我们采用3层全连接就可以轻易达到97%以上的精度。现在考虑经典的LeNet5，其网络结果如下（已经插入了量化与反量化层）。精度为99.2%，模型大小为0.25M。

   用基于tensor的量化方式量化后，模型大小变为0.07M，精度仍然是99.2%。

在前几年提出的BNN和TNN（二值和三值网络）的工作中也可以看出，MNIST这个小数据集对量化的容忍度很高，甚至BN这种极端量化方式也能达到和浮点几乎一样的性能。因此我们仅仅使用基于tensor的简单量化方式也取得了和浮点模型一样的性能也就不奇怪了。

1.3.2.2 Cifar10

   Cifar10相较于MNIST要更加复杂，因为通道数目变成了3，图片大小也稍大。为了尽可能少的修改，我们仍然考虑用MobileNetV2来实现。模型的代码仍然采用前面的MobileNetV2代码，只是需要根据CIfar10的特点改一些参数，我们参考了中的参数设置。校准的时候遍历了所有测试图片。精度和如下表。

	未量化（浮点）	基于tensor的量化	基于channel的量化
精度	94.53%	92.34%	94.25%

基于channel的量化精度上还是有个0.28%的损失，感觉还是不太爽。。。毕竟NVIDIA给的结果中ReNet用基于channel的量化精度损失都很小。

1.3.2.3 ResNet50 for ImageNet

  加载预训练的ResNet50，测试得到大小为102M，量化后为25M。设置batch size为100，校准的batch数目为32。量化前后的精度如下表所示。基于channel的量化相较于浮点的精度损失为0.46%，比NVIDIA提供的上面的表里面的精度下降要多。。。

model = quantization.resnet50(pretrained=True)

	未量化（浮点）	基于tensor的量化	基于channel的量化
精度	76.13%	74.93%	75.67%

参考文献

[1] 黎明灰烬，神经网络量化简介，2019.05.01。
[2] 返回主页把明天没收，Pytorch quantize 官方量化-VGG16 + MobileNetV2，2021.01.27。
[3] B. Jacob et al., “Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference,” 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018, pp. 2704-2713。
[4] Szymon Migacz, 8-bit Inference with TensorR, 2017.05.08。
[5] TensorFlow Lite 8 位量化规范。
[6] Raghuraman Krishnamoorthi,Quantizing deep convolutional networks for efficient inference: A whitepaper, 2018.
[7] QUANTIZATION.
[8] arleyzhang,TensorRT(5)-INT8校准原理,.2018.09.03.
[9] (BETA) STATIC QUANTIZATION WITH EAGER MODE IN PYTORCH
[10] Pytorch量化感知训练详解，2021.01.19
[11] Captain Jack，PyTorch 卷积与BatchNorm的融合，2020.05.27
[12] Owen718/mobileNet-v2_cifar10。