1. 有限域
1.1 有限域的characteristic。
对于一个有限域
F
F
F,记它的单位元为
e
e
e,则存在一个最小整数
p
p
p,使得
e
+
e
+
⋯
+
e
⏟
p
个
=
0
,
\underbrace{e+e+\cdots+e}_{p \text{个}}=0,
p个
e+e+⋯+e=0,则称
p
p
p是
F
F
F的characteristic。
■
\blacksquare
■
1.2 一个有限域的characteristic一定是质数(prime)。
■
\blacksquare
■
1.3 一个有限域的大小一定是characteristic的幂次(power),即
∣
F
∣
=
p
a
|F|=p^a
∣F∣=pa,其中
a
a
a是一个正整数。
■
\blacksquare
■
举例,一个有限域 G F ( 2 7 ) GF(2^7) GF(27)的characteristic是2,有限域元素个数为 2 7 2^7 27,是characteristic的幂次。
1.4 考虑一个有限域
F
F
F及其characteristic
p
p
p,则对任意两个
F
F
F中的元素有
(
a
+
b
)
p
=
a
p
+
b
p
.
(a+b)^p=a^p+b^p.
(a+b)p=ap+bp.
证明:
先利用二项公式打开括号,得到
(
a
+
b
)
p
=
∑
i
=
0
p
C
p
i
a
i
b
p
−
i
=
a
p
+
b
p
+
∑
i
=
1
p
−
1
C
p
i
a
i
b
p
−
i
.
(a+b)^p=\sum^{p}_{i=0}C^{i}_{p}a^ib^{p-i}=a^p+b^p+\sum^{p-1}_{i=1}C^{i}_{p}a^ib^{p-i}.
(a+b)p=i=0∑pCpiaibp−i=ap+bp+i=1∑p−1Cpiaibp−i.当
1
≤
i
≤
p
−
1
1\leq i\leq p-1
1≤i≤p−1时,
C
p
i
=
p
!
(
p
−
i
)
!
i
!
.
C^{i}_{p}=\frac{p!}{(p-i)!i!}.
Cpi=(p−i)!i!p!.因为
p
p
p是一个质数,因此上式中分母部分没有因子
p
p
p,所以
C
p
i
C^{i}_{p}
Cpi必然是
p
p
p的倍数,这意味着
C
p
i
a
i
b
p
−
i
=
0
C^{i}_{p}a^ib^{p-i}=0
Cpiaibp−i=0。综上,有
(
a
+
b
)
p
=
a
p
+
b
p
.
(a+b)^p=a^p+b^p.
(a+b)p=ap+bp.
■
\blacksquare
■
1.5 利用1.4很容易得到
(
a
1
+
a
2
+
⋯
+
a
n
)
p
k
=
a
1
p
k
+
a
2
p
k
+
⋯
+
a
n
p
k
.
(a_1+a_2+\cdots+a_n)^{p^k}=a^{p^k}_1+a^{p^k}_2+\cdots+a^{p^k}_n.
(a1+a2+⋯+an)pk=a1pk+a2pk+⋯+anpk.其中
a
i
∈
F
a_i\in F
ai∈F,
p
p
p是
F
F
F的characteristic,
k
k
k是正整数。
■ \blacksquare ■
1.6 考虑将1.4推广至多项式形式。假设
a
a
a和
b
b
b是两个
F
F
F中的元素,并且
p
p
p是
F
F
F的characteristic,则
(
a
x
+
b
y
)
p
=
a
p
x
p
+
b
p
y
p
.
(ax+by)^p=a^px^p+b^py^p.
(ax+by)p=apxp+bpyp.
证明:
由1.4的证明可知
(
a
x
+
b
y
)
p
=
a
p
x
p
+
b
p
y
p
+
∑
i
=
1
p
−
1
C
p
i
a
i
x
i
b
p
−
i
y
p
−
i
.
(ax+by)^p=a^px^p+b^py^p+\sum^{p-1}_{i=1}C^{i}_{p}a^ix^ib^{p-i}y^{p-i}.
(ax+by)p=apxp+bpyp+i=1∑p−1Cpiaixibp−iyp−i.因为
C
p
i
C^{i}_{p}
Cpi是
p
p
p的倍数,所以
C
p
i
a
i
x
i
b
p
−
i
y
p
−
i
=
0.
C^{i}_{p}a^ix^ib^{p-i}y^{p-i}=0.
Cpiaixibp−iyp−i=0.
■
\blacksquare
■
1.7 考虑一个多项式
f
(
x
)
=
f
0
+
f
1
x
+
f
2
x
2
+
⋯
+
f
n
x
n
,
f(x)=f_0+f_1x+f_2x^2+\cdots+f_nx^n,
f(x)=f0+f1x+f2x2+⋯+fnxn,其中
f
i
∈
F
f_i\in F
fi∈F.记
F
F
F的characteristic为
p
p
p,对于正整数
k
k
k,有
f
p
k
(
x
)
=
f
(
x
p
k
)
.
f^{p^k}(x)=f(x^{p^k}).
fpk(x)=f(xpk).
因此对于一个有限域GF(
p
n
p^n
pn),有
f
p
n
(
x
)
=
f
(
x
p
n
)
.
f^{p^n}(x)=f(x^{p^n}).
fpn(x)=f(xpn).
■
\blacksquare
■
1.8 不可约多项式:
一个
F
F
F上的多项式如果不能被另一个次数小于自己且大于0的
F
F
F上的多项式整除,则称该多项式为不可约多项式(irreducible polynomial)。
■
\blacksquare
■
1.9 最小多项式:
考虑一个有限域GF(
q
q
q)及其扩域GF(
q
m
q^m
qm),记
β
\beta
β是GF(
q
m
q^m
qm)中的一个元素。考虑等式
β
q
k
=
β
,
\beta^{q^k}=\beta,
βqk=β,记
d
d
d为满足该等式的最小正整数。则
β
\beta
β在GF(
q
q
q)上的最小多项式为
∏
i
=
1
d
−
1
(
x
−
β
q
i
)
.
\prod^{d-1}_{i=1}(x-\beta^{q^i}).
i=1∏d−1(x−βqi).
■
\blacksquare
■
1.10 设 β \beta β是GF( q m q^m qm)上的元素, ϕ ( x ) \phi(x) ϕ(x)使其在GF( q q q)上的最小多项式,则:
- 显然 ϕ ( β ) = 0 \phi(\beta)=0 ϕ(β)=0
- 可以证到 ϕ ( x ) \phi(x) ϕ(x)是拥有根 β \beta β的次数最小的GF( q q q)上的多项式(最小多项式名称的由来)。
-
ϕ
(
x
)
\phi(x)
ϕ(x)是不可约的(如果可约则有更低次多项式有根
β
\beta
β)。
■ \blacksquare ■
2. 生成矩阵与校验矩阵
2.1
生成矩阵和校验矩阵均是行满秩的。
■
\blacksquare
■
2.2 记一个线性码的最小距离为 d d d,则:
- 其校验矩阵 H H H存在 d d d列线性相关,每 d − 1 d-1 d−1列线性无关
- 生成矩阵 G G G的每 n − d + 1 n-d+1 n−d+1列无关
■ \blacksquare ■
2.3 记一个MDS码的最小距离为 d d d,则:
- 其校验矩阵 H H H的每 n − k n-k n−k列线性无关
- 生成矩阵 G G G的每 k k k列无关
■
\blacksquare
■
2.4 MDS码的对偶码也是MDS码。
■
\blacksquare
■
3. Syndrome decoding
考虑一个基于有限域
F
F
F的
(
n
,
k
)
(n,k)
(n,k)线性码,将其码字全部列出,记为一个陪集(coset)。在向量空间
F
n
F^n
Fn中除去该线性码的向量中选择重量最小的,与线性码的码字相加,得到新的向量,组成一个新的陪集。继续在
F
n
F^n
Fn的还没使用的向量中找重量最小的向量,与线性码的码字相加,得到一组新的向量,即一个新的陪集。重复这样的操作知道整个向量空间的向量全部被找出。

上图给了一个陪集的例子,第一行是一个线性码的所有码字,组成一个陪集。在组建第二行的陪集时,在第一行之外的向量中找到重量最小的向量00100,加到第一行上,得到新的陪集。重复操作得到所有向量。
syndrome decoding将先计算接收到的向量的校正子
s
=
y
H
T
.
s=\bm{y}H^T.
s=yHT.如果通过校正子找到对应的陪集,陪集首被认为就是错误向量。
■
\blacksquare
■
4. 汉明码与循环码
4.1 二元汉明码的定义。
考虑大小为
m
×
(
2
m
−
1
)
m\times (2^m-1)
m×(2m−1)的校验矩阵
H
H
H,他由
2
m
−
1
2^m-1
2m−1个GF(2)上的非零列向量组成。该校验矩阵对应一个汉明码,最小距离为
d
=
3
d=3
d=3。
■
\blacksquare
■
4.2 非二元汉明码的定义。
考虑有限域GF(
q
q
q),和一个GF(
q
q
q)上的大小为
m
×
q
m
−
1
q
−
1
m\times \frac{q^m-1}{q-1}
m×q−1qm−1的校验矩阵
H
H
H,他由
q
m
−
1
q
−
1
\frac{q^m-1}{q-1}
q−1qm−1个GF(
q
q
q)上的非零列向量组成,并且任意两个列向量不为倍数关系。该校验矩阵对应一个非二元汉明码,最小距离为
d
=
3
d=3
d=3。
对于GF(
q
q
q)上的非零列向量,乘上一个非零元素可以得到一个新的列向量,把这些列向量看做一组。因此一个GF(
q
q
q)上的长度为
m
m
m的列向量一共有
q
m
−
1
q
−
1
\frac{q^m-1}{q-1}
q−1qm−1组,非二元汉明码的校验矩阵的每一列对应一组。
■
\blacksquare
■
4.3 循环码的任意码字循环移位仍是该循环码的一个码字。
■
\blacksquare
■
4.4 一个
(
n
,
k
)
(n,k)
(n,k)循环码可以用一个次数为
n
−
k
n-k
n−k的生成多项式
g
(
x
)
g(x)
g(x)表示。记消息多项式为
m
(
x
)
m(x)
m(x),其次数为
k
−
1
k-1
k−1,则
(
n
,
k
)
(n,k)
(n,k)循环码的码字多项式为
c
(
x
)
=
m
(
x
)
g
(
x
)
.
c(x)=m(x)g(x).
c(x)=m(x)g(x).
■
\blacksquare
■
4.5 如何得到一个循环码的生成多项式?
考虑有限域GF(
q
q
q),则基于GF(
q
q
q)的多项式
x
n
−
1
x^n-1
xn−1有若干因式,每一个因式就是一个循环码的生成多项式,即每一个因式对应一个循环码。
■
\blacksquare
■
4.6 一个生成多项式为
g
(
x
)
=
g
0
+
g
1
x
+
⋯
+
g
n
−
k
x
n
−
k
g(x)=g_0+g_1x+\cdots+g_{n-k}x^{n-k}
g(x)=g0+g1x+⋯+gn−kxn−k的生成多项式为

他是生成多项式的系数向量移位得到的。
■
\blacksquare
■
4.7 根据4.5可知一个循环码的生成多项式整除
x
n
−
1
x^n-1
xn−1,记
h
(
x
)
=
x
n
−
1
g
(
x
)
.
h(x)=\frac{x^n-1}{g(x)}.
h(x)=g(x)xn−1.则
h
(
x
)
h(x)
h(x)称为该循环码的校验多项式。记
h
(
x
)
=
h
0
+
h
1
x
+
⋯
+
h
k
x
k
,
h(x)=h_0+h_1x+\cdots+h_kx^k,
h(x)=h0+h1x+⋯+hkxk,则该循环码的校验矩阵为
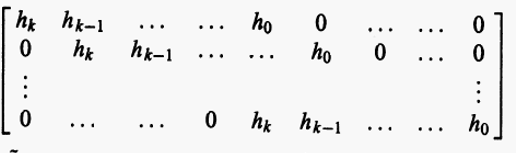
■
\blacksquare
■
4.8 一个生成多项式为
g
(
x
)
g(x)
g(x)的循环码的校验多项式为
h
(
x
)
=
x
n
−
1
g
(
x
)
h(x)=\frac{x^n-1}{g(x)}
h(x)=g(x)xn−1,他的反多项式(reciprocal polynomial)记为
h
~
(
x
)
=
x
k
h
(
x
−
k
)
=
h
k
+
h
k
−
1
x
+
⋯
+
h
0
x
k
,
\tilde{h}(x)=x^kh(x^{-k})=h_k+h_{k-1}x+\cdots+h_0x^k,
h~(x)=xkh(x−k)=hk+hk−1x+⋯+h0xk,该反多项式是该循环码的对偶码的生成多项式,即该对偶码也是一个循环码,并且该对偶码的生成矩阵为4.7中的校验矩阵。
■
\blacksquare
■
5. 码的个数
5.1 有限域
F
q
F_q
Fq上的一个行满秩的大小为
m
×
n
m\times n
m×n的矩阵的个数为
∏
i
=
0
m
−
1
(
q
n
−
q
i
)
.
\prod^{m-1}_{i=0}(q^n-q^i).
i=0∏m−1(qn−qi).逐行构建,每一行不能是之前行的线性组合。
■
\blacksquare
■
5.2 给定一个
(
n
,
k
)
(n,k)
(n,k)线性码,其生成矩阵的个数为
∏
i
=
0
k
−
1
(
q
k
−
q
i
)
.
\prod^{k-1}_{i=0}(q^k-q^i).
i=0∏k−1(qk−qi).逐行构建,每一行不能是之前行的线性组合,并且行向量的总数为
2
k
2^k
2k。
■
\blacksquare
■
5.3 根据5.1 和5.2 ,有限域
F
q
F_q
Fq上的
(
n
,
k
)
(n,k)
(n,k)的线性码的个数为
∏
i
=
0
m
−
1
(
q
n
−
q
i
)
∏
i
=
0
k
−
1
(
q
k
−
q
i
)
=
(
q
n
−
1
)
(
q
n
−
1
−
1
)
⋯
(
q
n
−
k
+
1
−
1
)
(
q
k
−
1
)
(
q
k
−
1
−
1
)
⋯
(
q
−
1
)
.
\frac{\prod^{m-1}_{i=0}(q^n-q^i)}{\prod^{k-1}_{i=0}(q^k-q^i)}=\frac{(q^n-1)(q^{n-1}-1)\cdots(q^{n-k+1}-1)}{(q^k-1)(q^{k-1}-1)\cdots(q-1)}.
∏i=0k−1(qk−qi)∏i=0m−1(qn−qi)=(qk−1)(qk−1−1)⋯(q−1)(qn−1)(qn−1−1)⋯(qn−k+1−1).
■
\blacksquare
■
5.4 二元汉明码的所有校验矩阵个数为
n
!
.
n!.
n!.给定一个二元汉明码,其校验矩阵个数为
∏
i
=
0
m
−
1
(
q
m
−
q
i
)
.
\prod^{m-1}_{i=0}(q^m-q^i).
i=0∏m−1(qm−qi).因此二元汉明码的个数为
n
!
∏
i
=
0
m
−
1
(
q
m
−
q
i
)
.
\frac{n!}{\prod^{m-1}_{i=0}(q^m-q^i).}
∏i=0m−1(qm−qi).n!
■
\blacksquare
■
5.5 非二元汉明码的所有校验矩阵个数为
(
q
−
1
)
n
n
!
.
(q-1)^nn!.
(q−1)nn!.这里的
(
q
−
1
)
n
(q-1)^n
(q−1)n是因为每一列都可以乘上一个非零的其他元素得到一个新的列。给定一个非二元汉明码,其校验矩阵个数为
∏
i
=
0
m
−
1
(
q
m
−
q
i
)
.
\prod^{m-1}_{i=0}(q^m-q^i).
i=0∏m−1(qm−qi).因此二元汉明码的个数为
(
q
−
1
)
n
n
!
∏
i
=
0
m
−
1
(
q
m
−
q
i
)
.
\frac{(q-1)^nn!}{\prod^{m-1}_{i=0}(q^m-q^i).}
∏i=0m−1(qm−qi).(q−1)nn!
需要注意非二元汉明码的码长为
n
=
q
m
−
1
q
−
1
n=\frac{q^m-1}{q-1}
n=q−1qm−1.
■
\blacksquare
■
5.5 一个
F
q
F_q
Fq上的循环码的个数与
F
q
F_q
Fq上的多项式
x
n
−
1
x^n-1
xn−1的因式的个数相同。
■
\blacksquare
■
参考文献
[1] Roman S . Coding and information theory,1992。
[2] 林舒,差错控制编码。







 本文介绍了有限域的基本概念,如特征、质数特征、域的大小、运算性质以及不可约多项式和最小多项式。此外,深入探讨了生成矩阵与校验矩阵在编码理论中的角色,包括MDS码和汉明码的构造,以及循环码的生成与校验过程。最后,涉及了码的数量计算和不同类型的编码如汉明码和循环码的详细讨论。
本文介绍了有限域的基本概念,如特征、质数特征、域的大小、运算性质以及不可约多项式和最小多项式。此外,深入探讨了生成矩阵与校验矩阵在编码理论中的角色,包括MDS码和汉明码的构造,以及循环码的生成与校验过程。最后,涉及了码的数量计算和不同类型的编码如汉明码和循环码的详细讨论。
















 204
204

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








