【现代通信原理笔记】7 差错控制编码（信道编码）

【现代通信原理】7 差错控制编码（信道编码）

重点

• 检错、纠错
• 检纠错能力两个公式。纠错能力 t、检错能力 e（重要）
• 差错控制方式：前向纠错，检错重传，混合纠错
• 分组码：校验矩阵、监督码元、效率、码长、（最小）码距、码重
• 恒比码正反码（仅了解）
• 线性分组码：线性码、汉明码、校正子的作用。清楚原理
• H 矩阵，G 矩阵 构成，转换关系（重要）

部分内容结合计算机网络原理

• 第 10 章：检错与纠错（线性分组码、CRC）
• 第 11 章：数据链路控制（ARQ 系统）

概述

通信的可靠性

可靠性增加，有效性减小

要将质量要求与误码率两者匹配起来

误码

• 针对乘性干扰：采用均衡等措施
• 针对加性干扰：合理选择调制/解调方法、增大发射功率
• 对剩余的误码：采用差错控制、交织等措施，加以纠正

差错控制方式

应根据信道类型、对实时性和误码率的要求等因素来选择。

信道类型 — 根据错码的不同分布规律分为：

• 随机信道:错码是随机独立出现的
• 突发信道:错码是成串集中出现的
• 混合信道:既有随机错码又有突发错码

差错控制方式：

• 检错重发——自动请求重发(ARQ)
• 前向纠错（英语：forward error correction，缩写 FEC）前向纠错是一种差错控制方式，即纠错编码
• 混合纠错

技术措施：

• 纠错编码
• 纠错策略 —— 即以上差错控制方式

3 种自动请求重发(ARQ)系统

• 停止等待 ARQ 系统

• 拉后 ARQ 系统​

  • 回退 N 帧 ARQ
  • 选择重发 ARQ 系统
  • 选择性重复 ARQ

参考计网

编码器 对输入的信码进行分组编码（加入校验元）后发送。若收到接收端的重发(NAK)指令，执行重发。

译码器 对接收码校验，若发现有错，则通过反向信道发送一个 重发(NAK)指令，指示发送端重发。若无错，则发送确认(ACK) 指令，指示发送端正常发送。

ARQ 的主要优点：与前向纠错 (FEC) 方法相比

• 能抵抗大误码率，适应不同特性的信道；
• 检错的计算复杂度较低；

ARQ 的主要缺点：

• 重发使得 ARQ 系统的传输效率降低。
• 需双向信道来重发，不适用单向信道和一点到多点的通信系统

第 1 讲 基本原理及简单编码

校验（监督）码元：发送端在信息码元序列中增加一些差错控制码元，以便收端判断正误，它们被称为校验码元。校验码元位数不同，检错或纠错能力就不同。

编码效率（简称码率）：设编码序列中信息码元数量为 k，总码元数量为 $n(n>k)$ ，则比值 $R=k/n$ 就是码率。校验码元数 $r=n-k$。

差错控制编码表面上降低有效性，换取更低误码率，提高可靠性。但信息速率可能更接近信道容量

分组码基本原理

分组码：把一个长数据文件分成若干个长度相等的信息码组，在每个码组后加上校验码。与分组码并称的另一种码是卷积码。

系统码：信息位保持不变，在其后加上校验位的纠错码

非系统码：编码码组中无对应信息位（信息位和校验位交叉）

许用码组

禁用码组：接收端一旦收到禁用码组，就认为出现了错码。

校验码元：系统码的校验码元冗余

码长 ($n$)：码组（码字）中的码元个数。

码重 ($W$)：码组 $a$ 中“1”的数目，$w(a)$。

码距 ($d$)： 两个码组 a、b 对应位上不同值的个数，称为码组 的距离 $d(a,b)=w(a+b)$。—又称汉明距离。（“+”按位模 2 加）

最小码距 ($d_0$)：某种编码各个码组之间距离的最小值

最小码距 $d_0$ 和检纠错能力的关系（可以画图方便理解）

• 检 e 个错码 $d_0⩾e+1$
• 纠 t 个错码 $d_0⩾2t+1$
• 纠 t 个错码 & 检 e 个错码 $d_0⩾e+t+1(e>t)$

1.1 奇偶校验（监督）码

1.2 二维奇偶校验（监督）码（方阵码）

1.3 恒比码(等重码)（仅了解）

“1”的数目与“0”的数目之比保持恒定。

1.4 正反码（仅了解）

每个码组的校验位数等于信息位数，校验位值由信息码中的“1” 的数目确定：

• 当信息码中有奇数个“1”时，校验位是信息位的重复；
• 当信息码中有偶数个“1”时，校验位是信息位的反码；

该码能够严格地纠正任意 1 位错码，码率为 1/2。

校验和

计网内容

反码、求和、0

第 2 讲 线性分组码

• 线性码：按照一组线性方程构成的代数码。即每个码字的校验码元是信息码元的线性组合。
• 代数码：建立在代数学基础上的编码。
• 分组码：每一码组的校验码元仅与本组中的信息码元有关。
• 线性分组码：按照一组线性方程构成的分组码。例如，奇偶校验码就是一种 $(n,n-1)$ 线性分组码。

符号表示：一种码若码长是 n，其中信息码有 k 位，称为 $(n,k)$ 码，如 (7, 4) 码。以下以 (7, 4) 码为例。

信息码向量 $\vec{m}=(m_3,m_2,m_1,m_0)$

发送码向量 $\vec{A}=(a_6,a_5,a_4,a_3,a_2,a_1,a_0)$

接收码向量 $\vec{B}=(b_6,b_5,b_4,b_3,b_2,b_1,b_0)$

汉明码

校正子：s

校验关系式：

若 s=0，认为无错（偶校验时）；若 s=1，认为有错 。—— 检错

若要构造具有纠错能力的 (n, k) 码，则需增加校验元的数目。 s (即方程)的个数等于校验元位数 r。

对于 (n, k) 线性分组码，若希望用 r=n-k 个校验码元构造出 r 个校验

关系式来指出一位错码的 n 种可能的位置，则 r 必须满足：

$$2^r-1\ge n或2^r\ge k+r+1$$

-1 是因为还有一种可能性没有错

当“=”成立时，构造的线性分组码称为汉明码——能纠 1 位错码高效线性分组码

$$(n,k)=(2^r-1,2^r-1-r)$$

信息元和校验 (parity check)元是平等的

• 汉明码特点

码参数：

式 $2^r-1\ge n$ 中的等号成文. 即 $(n,k)=\left(2^r-1,2^r-1-r\right)$，$ r$ 是不小于 3 的任意正整数

最小码距:

$$d_0=3\text{ (纠1或检2) }$$

编码效率:

$$R_c=\frac{k}{n}=\frac{n-r}{n}=1-\frac{r}{2^r-1}$$

当 $n$ 很大时, $r$ 相对很小, 码率 $R_{\mathrm{c}}$ 接近 1 。

可见，汉明码是能够纠正 1 位错码的最高效线性分组码。

线性分组码一般原理

H 校验矩阵

若矩阵由一个小矩阵和满秩的单位阵组合而成，则称它为典型矩阵。

H 的各行是线性无关的。否则得不到 r 个线性无关的校验关系式。

若一矩阵能写成典型阵形式 $[P{I}_r]$，则其各行一定是线性无关的。

G 生成矩阵

将上面汉明码例子中的校验位计算公式： 改写成矩阵形式：

式中，$Q$ 为一个 $k\times r$ 阶矩阵，它是 $P$ 的转置，即

$$Q=P^{\text{T}}$$

可见，给定信息位后用信息位行向量乘矩阵 $Q$ 就产生校验位。

将 $Q$ 的左边加上一个 $k\times k$ 阶单位方阵，就构成矩阵:

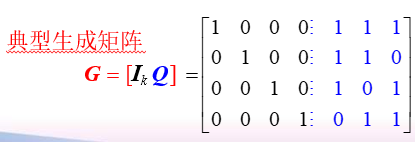
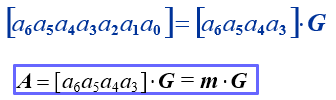
具有 $[I_{k}Q]$ 形式的 $G$ 称为典型生成矩阵。由典型得 $G$ 到的码称为系统码

系统码：信息位保持不变，在其后加上校验位的纠错码

G 矩阵的性质

① G 矩阵是 $k\times n$ 矩阵。

② G 的各行是线性无关的；它的各行本身就是一个码组。

∴ 若有 k 个线性无关的码组，则可用其组成生成矩阵 G，生成其余码组。

可以看出：任一码组 A 都是 G 的各行的线性组合。G 共有 k 行，可以组合出 $2^k$ 种不同的码组 A。

G 和 H 的关系

非典型的 G 或 H 可以通过行线性变换变成典型的 G 、H ，仍然对应于该编码。可以由此进行 G 、H 互求。

校正子与错误图样

则发送码组和接收码组之差就是错误图样

设发送码组为一个 $n$ 元行向量 $A$, 接收码组行向量 $B$

$$\mathbf{A}=\left[\begin{array}{lll}{a}_{n-1}{a}_{n-2}& \cdots & a_1{a}_0\end{array}\right]\mathbf{B}=\left[b_{n-1}{b}_{n-2}\cdots b_1{b}_0\right]$$

则发送码组和接收码组之差就是错误图样:

$$\mathbf{B}-\mathbf{A}=\mathbf{E}=\left[\begin{array}{ll}{e}_{n-1}{e}_{n-2}& \cdots e_1{e}_0\end{array}\right]$$

式中：

$$e_i=\{\begin{array}{lll}0,& \text{ 当 }{b}_i=a_i& \text{ 表示该接收码元无错 }\\ 1,& \text{ 当 }{b}_i\ne a_i& \text{ 表示该接收码元有错 }\end{array}$$

$S$ 称为校正子（伴随式）。

校正子 $S$ 与错误图样 E 一一对应，而与发送码 A 无关。

(n,k) 线性分组码译码的三个步骤：

1. 由接收码组 B 计算：$ S = H · B^T$
2. 由 $S$ 找到错误图样 E；
3. 由公式 $A=B–E$ 得到译码器译出的码组。

注：若 B 中错误超过纠错能力，则也可能 $S=H\cdot B^T=0$。此种错误不可检。

线性分组码的性质

① 封闭性

一种线性码中任意两个许用码组 $A_1$ 和 $A_2$ 之和 $(A_1+A_2)$ (按位模 2 加) 后的码组，仍为该码中的一个许用码组。

证明：若 $A_1$ 和 $A_2$ 是两个码组，则有 $H\cdot A_1^{\text{T}}=0$ 和 $H\cdot A_2^{\text{T}}=0$，

将两式相加，有 $H\cdot A_1^{\text{T}}+H\cdot A_2^{\text{T}}=H\cdot (A_1+A_2{)}^{\text{T}}=0$（证毕）

② 最小距离

码的最小距离就是码的最小重量

证明：根据码的封闭性，可知两个码组 $A_1$ 和 $A_2$ 之间的距离(即对应位不同的数目)必定是另一个码组 $A_1+A_2$ 的重量(即“1”的数目)。

注：从生成矩阵 G 的最小行重量常常就能判断最小距离

第 3 讲 循环码

具体内容略

循环性：指任一码组循环移位（将最左端的一个码元移至右端， 或反之），仍为该码中的一个码组；

循环码：除了具有线性分组码的一般性质外，还具有循环性

循环冗余校验(CRC)码

计网重点

• 数据字：$d(x)$
• 码字：$c(x)$
• 生成多项式：$g(x)$
• 校正子：$s(x)$
• 差错：$e(x)$

$$\frac{接受的码字}{g(x)}=\frac{c(x)}{g(x)}+\frac{e(x)}{g(x)}$$

差错检验能力

• 单个位差错

  • 如果 $g(x)$ 项数至少为 2 且 $x^0$ 的系数为 1，那么所有的单个位差错都能捕捉到。

• 两个独立的单个位差错

  • 如果生成多项式不能整除 $x^t+10\le t\le n-1$，那么所有的独立双差错都能被检测到

• 奇数个差错

  • 包含因子 $x+1$ 的生成多项式能检测到所有奇数个差错

• 突发性差错 （$L$：差错长度； $r$：校验位数）

  • 所有 $L\le r$ 的突发性差错都能被检测到
  • 所有 $L=r+1$ 的突发性差错有 $1-(1/2{)}^{r-1}$ 的概率会被检测到
  • 所有 $L>r+1$ 的突发性差错有 $1-(1/2{)}^r$ 的概率会被检测到

高性能生成多项式 $g(x)$ 需要有以下特性：

• 至少有 2 项
• $x^0$ 项的系数是 1
• 它不能整除 $x^t+1$，（t 是 2 到 n-1 之间）
• 它有因子 $x+1$

参考

作业

（模二运算？）