0-1背包问题

对于0-1背包问题核心问题是：判断当前这个物品我是放入背包之后可获取更大价值，还是不放入会获取更大价值

情况1：放入了该物品n

总价值 = 放入该物品的价值 + 背包剩余容量可放入的最大价值

情况二：没有放入该物品

总价值 = 前n-1件物品的价值

因为前n-1件物品的最优解是已经知道了的，所以只需要比较这两种情况就可以知道当背包容量为m时，前n件物品的可放入背包的最优解，那么从n=0、1....开始的情况是很简单的，很容易获取到，所以后面的大容量多物品只需要借助前面的已知最优解的基础上就很容易得到其最优解。

#include <iostream>
#include <vector>
#include <list>
using namespace std;

/*
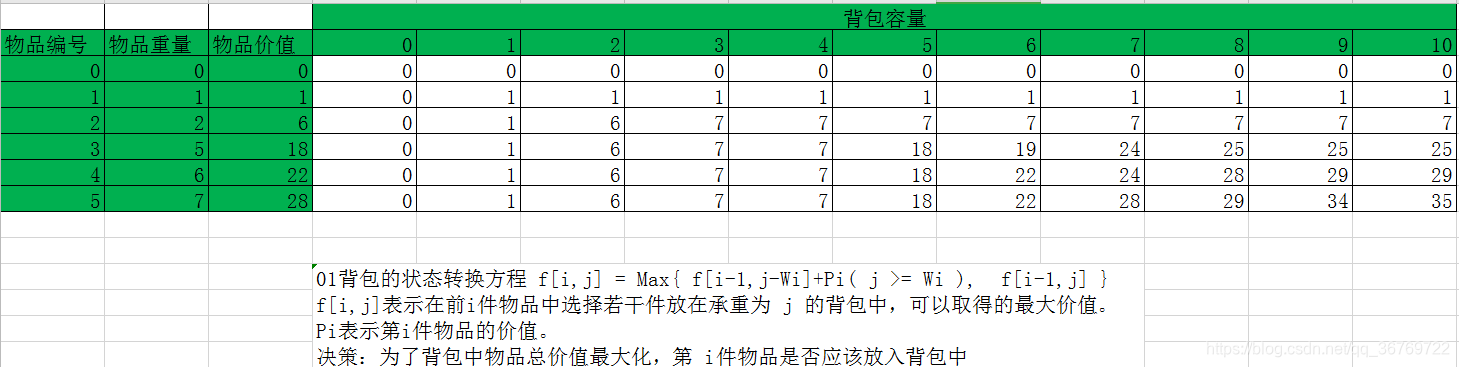
01背包的状态转换方程 f[i,j] = Max{ f[i-1,j-Wi]+Pi( j >= Wi ),  f[i-1,j] }
f[i,j]表示在前i件物品中选择若干件放在承重为 j 的背包中，可以取得的最大价值。
Pi表示第i件物品的价值。
决策：为了背包中物品总价值最大化，第 i件物品应该放入背包中吗 ？
*/
struct Goods
{
	int weight;		//物品重量
	int value;			//物品价值
};
const int maxCapacityPackage = 10;
int tempArray[6][maxCapacityPackage + 1] = { 0 };
//Goods goods[6] = { {0,0}, {2,6},{2,3},{6,5},{5,4},{4,6} };
Goods goods[6] = { {0,0}, {1,1},{2,6},{5,18},{6,22},{7,28} };
vector<list<int>> answer(maxCapacityPackage+1);		//存放各种背包容量的物品方案选择
void Answer(int capacity,int goodsIndex,list<int>& curCapacityAnswer)
{
		for (int row = goodsIndex; row > 0; row--)
		{
			if (tempArray[row][capacity] != tempArray[row - 1][capacity])
			{
				curCapacityAnswer.push_back(row);
				return Answer(capacity - goods[row].weight, row - 1,curCapacityAnswer);
			}
		}
}


int main()
{

	for (int capacity  = 1; capacity <= maxCapacityPackage; capacity++)
	{
		for (int goodsIndex = 1; goodsIndex <= 5; goodsIndex++)
		{
			//当前物品不能装入背包，那么和上一件物品装入最大值一样
			if (goods[goodsIndex].weight > capacity)
			{
				tempArray[goodsIndex][capacity] = tempArray[goodsIndex - 1][capacity];
			}
			else
			{
				//情况一：装入当前物品总价值
				//最大价值为：当前物品价值+背包剩余空间的前N-1件物品的最大价值
				int  canditionOneValue = goods[goodsIndex].value+ tempArray[goodsIndex-1][capacity -goods[goodsIndex].weight];
				//情况二：不装入当前物品的总价值
				//最大价值为：和不装入当前物品的最大价值一样
				int canditionTwoValue = tempArray[goodsIndex - 1][capacity];
				//计算更大价值装法
				tempArray[goodsIndex][capacity] = canditionOneValue > canditionTwoValue ? canditionOneValue : canditionTwoValue;
			}
		}
	}

	cout << "各种容量背包可装入物品的最大价值：" << endl;
	cout << "id\t容量\t价值\t\t";
	for (int capacity = 0; capacity <= maxCapacityPackage; capacity++)
	{
		cout << capacity << "\t";
	}
	cout << endl<<"-\t-\t-\t-\t";
	for (int capacity = 0; capacity <= maxCapacityPackage; capacity++)
	{
		cout << "-" << "\t";
	}
	cout << endl;
	for (int goodsIndex = 0; goodsIndex <= 5; goodsIndex++)
	{
		cout <<goodsIndex<<"\t"<< goods[goodsIndex].weight <<"\t"<< goods[goodsIndex].value<<"\t|\t";
		for (int capacity = 0; capacity <= maxCapacityPackage; capacity++)
		{
			cout<<tempArray[goodsIndex][capacity] << "\t";
		}
		cout << endl;
	}
	cout <<endl<< "选择方案为：";
	for (int capacity = 1; capacity <= maxCapacityPackage; capacity++)
	{
		Answer(capacity, 5,answer[capacity]);
		cout <<endl<< "容量为" << capacity << "的最大价值方案为：";
		for (auto iter=answer[capacity].begin(); iter!= answer[capacity].end(); iter++)
		{
			cout<< *iter<<"\t";
		}
	}
}