倪震华教授版《振动力学》学习（一）

绪论

1. 三种问题

系统物理参数：M K C
系统模态参数：固有频率与振型
激励：输入
响应：输出
已知系统、激励，求响应。
已知激励、响应，求系统。物理参数识别：识别系统的M K C；模态参数识别/实验模态分析：识别系统的固有频率与振型
已知系统、响应，求激励。
我最近对第二种很感兴趣，所以买了本《模态分析理论与应用》来看。

2. 自由度数

自由度数是指描述系统一切部位在任何瞬时运动所需要的坐标数

3. 分布参数系统与集中参数系统

取决于系统物理参数是均匀分布还只在某一处或几处集中

4. 振动种类

线性振动、非线性振动：振动方程是线性微分方程还是非线性微分方程

第一章 简谐振动与频谱分析

1. 简谐振动及其合成

简谐振动的位移响应用简谐函数表示

两个同频率的简谐函数的合成仍是简谐函数，且保持原频率
两个频率接近的简谐函数的合成是一个拍，红色部分是其包络线

我认为频率比不论是有理数还是无理数，其合成函数都是一个周期函数

2. 傅里叶级数

简谐函数表示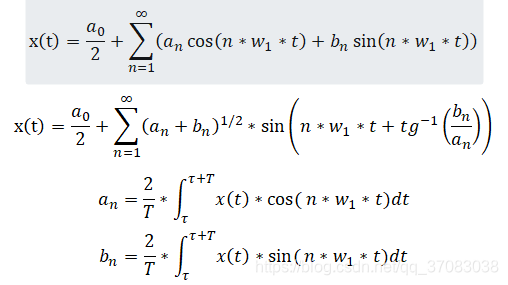

复数表示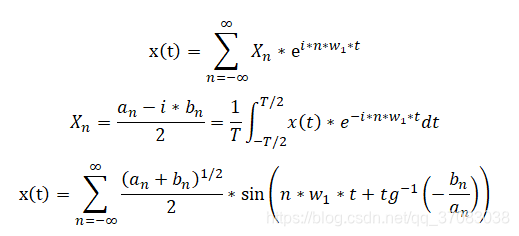

3. 傅里叶积分

非周期函数
一段周期函数就是非周期函数，因为他只在一段时间内是周期函数，其余时间为0。
将该非周期函数当作周期为无穷的函数后，只要x(t)满足狄利克雷条件且绝对可积，即可变换到频域。

傅里叶级数用于：时间无穷的连续周期函数
傅里叶积分用于：时间无穷的连续非周期函数
而我们平时软件处理的是时间有限的离散函数，利用DFT可以将其变换到频域
硬件处理的是时间有限的连续函数，对于硬件如何处理我没接触过

4. 脉冲力

δ函数：t=0时为∞，其余时刻为0
脉冲力：作用时间无限短，而具有有限冲量的力。作用空间集中，作用时间集中。
集中力：作用空间集中。
脉冲力与集中力可由δ函数描述。

第二章 单自由度系统

1.常微分方程的解

前面已说过，同频率的简谐函数可以合成一个简谐函数

2.能量法

阻尼导致机械运转时产生热量，消耗系统能量，对于可看作能量守恒即不计阻尼的系统，可以用能量法求解
考虑惯性元件的动能与弹性元件的势能

3. 瑞利法

同时考虑弹性元件的动能

4.等效质量、等效刚度

等效刚度：系统在坐标方向产生单位位移而需要在坐标方向上施加的力
等效质量：系统在坐标方向产生单位加速度而需要在坐标方向上施加的力
其实就是求系统的刚度与质量，系统可能包含多个弹性元件、多个惯性元件

5. 有粘性阻尼的自由振动

阻尼即阻力：摩擦阻尼、电磁阻尼、介质阻尼、结构阻尼等
粘性阻尼/粘滞阻尼Pd：在流体中低速运动或沿润滑表面滑动的物体，通常认为受到粘性阻尼，其与相对速度成正比
Pd=c*v，c为(粘性)阻尼系数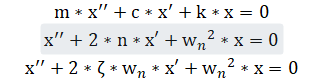


n为衰减系数，ζ为相对阻尼系数

讨论其根，会有三种形式，过阻尼、欠阻尼、临界阻尼
注：可直接写出特征方程或者将带入得到特征方程，求解特征方程可得到其根，再分别讨论

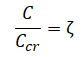
ζ也称阻尼比

临界阻尼Ccr只取决于系统本身的质量与刚度

欠阻尼系统
两根为共轭复数
阻尼固有频率

6. 常微分方程的解

根据特征根可写出微分方程的解
根据特征根可判断系统的稳定性，特征根在右半平面则振动不是稳定的

过阻尼

临界阻尼

欠阻尼

第三章 单自由度系统的强迫振动

激励：直接作用到结构上的力、支撑的运动
简谐力激励时系统的响应包括：初始条件引起的自由振动、伴随强迫振动的自由振动、等幅的稳态强迫振动。如果初始条件为0，那么也就不存在第一种振动了。自由振动会逐渐衰减，称之为其响应为瞬态响应，最终只剩下强迫振动，称之为稳态响应。

1.振幅放大因子

又要研究微分方程的解了，哈哈

频率比

振幅放大因子，共振时的振幅放大因子也称品质因子Q

共振峰：β-λ曲线在λ=1附近的曲线
Q反映了系统阻尼大小与共振峰的陡峭程度

2.用旋转矢量来表示稳态振动

3.机械阻抗

简谐激振时复数形式的输入与输出之比。其倒数为幅频响应函数或频率响应函数，也叫导纳
位移阻抗：动刚度 
位移导纳：动柔度
速度阻抗：简称阻抗
加速度阻抗：视在质量

4. 微分方程

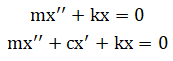
这是无激励时讨论的两个方程

周期激励时讨论的两个方程

计算下面问题的通解

方1：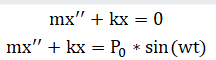

计算方程1的通解
方程2的特解
两个解之和即为通解，再将初始条件带进去，即为最终结果
方2：

计算方程1的通解，再将初始条件带进去
计算方程2的通解，再将初始条件带进去
两个解之和即为通解，即为最终结果

观察最终结果，会发现有四项，前两项为初始条件引起的自由振动，第三项为自由伴随振动，第四项为稳态强迫振动
由于该方程无阻尼项，自由振动是不会减小的

对于有阻尼的系统，两种自由振动前面就都会乘一个衰减项了

5. 迟滞回线

两种迟滞回线
粘性阻尼Pd与x绘制的曲线，其面积为一周期运动消耗的能量，当消耗的能量与振幅平方呈正比时，迟滞回线为椭圆
应力与应变绘制的曲线，其面积为一周期运动消耗的能量，当消耗的能量与应变幅度平方呈正比时，迟滞回线为椭圆

还有两种学过的闭合的曲线：
磁滞回线，B与H绘制的曲线
本构曲线，应力与应变绘制的曲线

6. 阻尼

粘性阻尼，后三个为非线性阻尼，他们是外面的介质对结构产生的阻力
干摩擦阻尼/库伦阻尼
低粘度流体阻尼
指数阻尼

结构阻尼/迟滞阻尼：材料内摩擦
结构阻尼比位移在相位上超前Pi/2，大小与位移成正比

称为复刚度

https://mp.weixin.qq.com/s/XCT14gJvIdVVI_1KFTg0lQ

7. 周期激励与非周期激励

周期激励可看作多个简谐激励的合成，施加周期激励相对于分别施加简谐激励后的响应和
非周期激励可看作多个脉冲激励的积分，施加非周期激励相对于分别施加脉冲激励后的响应和
杜哈梅积分：任意激励的响应可看作所有脉冲响应的和
Borel定理：线性系统对任何激励的响应等于其脉冲响应与激励的卷积

8. 传递函数、复频响应函数、脉冲响应函数

传递函数：系统输出的拉氏变换与输入拉氏变换之比
复频响应函数：也称频响函数，频率响应函数 FRF。系统输出的傅氏变换与输入傅氏变换之比
脉冲响应函数：脉冲力激励时的时域响应函数

9. 响应谱

最大响应值与系统的关系
最大响应值与激励的某一参数的关系