可变形卷积

可变形卷积

论文下载地址：https://openaccess.thecvf.com/content_ICCV_2017/papers/Dai_Deformable_Convolutional_Networks_ICCV_2017_paper.pdf
代码地址：https://github.com/4uiiurz1/pytorch-deform-conv-v2/blob/master/deform_conv_v2.py

一.普通卷积

我们先看一看普通卷积的计算过程，可以更好的去理解可变形卷积的实现过程。普通卷积的计算公式如下：
$$y(P_0)=\sum _{P_n\in R}W(P_n)\ast X(P_0+P_n)$$
R域定义了卷积操作的kernel size和dilation
假设使用3*3的卷积核，R = {(−1, −1), (−1, 0), . . . , (0, 1), (1, 1)

$P_0$表示窗口的中心位置，R是相对位置坐标矩阵，$P_n$则是其周围距离不超过1个像素的相对位置的枚举值。

卷积计算就是图像中有一个给定的滑动窗口，与kernel中的权重做加权和。即中心坐标$P_0$加上相对位置坐标$P_n$,这样去迭代出窗口中每一个像素的坐标，$X(P_0+P_n)$就表示取每一个位置的像素，而$W(P_n)$就是每一个位置像素对应的权重，将所有的$W(P_n)\ast X(P_0+P_n)$累加输出一个位置的像素值。

二.为什么使用可变形卷积

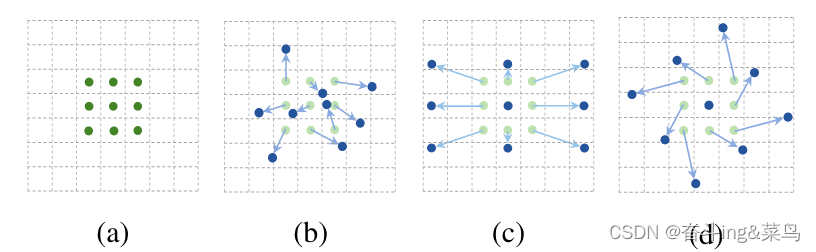
传统的卷积操作是将特征图分成一个个与卷积核大小相同的部分，然后进行卷积操作，每部分在特征图上的位置都是固定的。这样对于形变比较复杂的物体，使用这种卷积的效果就可能不太好了。可变形卷积基于一个平行的网络来学习偏移，让卷积核在输入特征图能够发散采样，使网络能够聚焦目标中心，从而提高对物体形变的建模能力。
标准卷积中的固定感受野(a)和可变形卷积中的自适应感受野(b)的图解，使用两层。顶部:顶部特征图上的两个激活单元，在两个不同比例和形状的对象上。激活来自一个3 × 3的过滤器。中间:3 × 3滤波器在上述特征图上的采样位置。另外两个激活单元被突出显示。下图为两级3 × 3滤波器在上述特征图上的采样位置。突出显示的位置对应于上面突出显示的单元。

三.什么是可变形卷积？

与普通卷积不同的是可变形卷积计算过程中添加了offset来适应图像特征

可变形卷积的计算公式如下：
$$y(P0)=\sum _{P_n\in R}W(P_n)\ast X(P_0+P_n+\Delta P_n)$$
y是新的像素坐标，$\Delta P_n$是偏移量offset，$P_0+P_n+\Delta P_n$是新的坐标，$X(P_0+P_n+\Delta P_n)$表示取出该位置的像素值，$W(P_n)$表示卷积核相对$P_0+P_n+\Delta P_n$位置像素的权重值。迭代相加所有位置的值$W(P_n)\ast X(P_0+P_n+\Delta P_n)$输出结果像素值。

四.怎样实现可变形卷积

实现过程详解

首先看一下偏移计算全过程图：

使用3x3的卷积核示范某个window的可变形卷积计算过程。我们将原图像坐标$P_0$（3，3）处的像素作为window的中心坐标，记为（0，0），计算其R范围中各坐标像素的偏移量和最终的偏移后像素值。我们以R域左上角（-1，1）处取值为例，（-1，1）在整个图像中的位置坐标为$P_0+P_n$=（2，4），可变形卷积会学习一个偏移量offset,即$\Delta P_n$=（0.9，1），与原始坐标（2，4）相加得到得到新的像素点坐标为$P_0+P_n+\Delta P_n$=（2.9，5），再采用双线性插值来处理偏移后新的像素点的像素值（对于分数阶的偏移量，在可变形卷积中采样需要通过双线性插值来实现。这个过程可以通过计算偏移后位置 $P_0+P_n+\Delta P_n$ 和周围最近邻像素的距离权重，并进行加权平均来估计偏移后位置处的像素值。）。
图解如下：

得到所有偏移后的位置和偏移后的像素取值计算出所有位置的坐标和像素值之后，每个位置的像素与卷积核权重相乘的到最终输出像素值。如下所示：
$$\left[\begin{array}{ccc}{V}_1& V_2& V_3\\ V_4& V_5& V_6\\ V_7& V_8& V_9\end{array}\right]\ast \left[\begin{array}{ccc}{W}_1& W_2& W_3\\ W_4& W_5& W_6\\ W_7& W_8& W_9\end{array}\right]=[value]$$
第一个矩阵表示偏移后window中各位置取得的各像素值，第二个矩阵表示卷积核的权重W，两个矩阵相乘的到最终要取的元素值。

重点过程解释
1.计算offset
使用3x3，输出通道数为2xkernel_size x kernel_size的卷积核计算offset(偏移量)

计算偏移量的卷积输出通道out_channel数和可变形卷积的输出通道数不一样，
这里的out_channel数是2倍的kernel _size 的平方，因为偏移是x和y轴都进行的。假设我们使用RGB的图像，使用3*3的卷积进行处理（步长和padding取值都为1），那么输入的通道数为3，输出的通道时就为18。蓝色部位为某一个可变形卷积的窗口，这个窗口做卷积输出像素channel数为18，将对应的channel拿出来reshape一下，得到偏移R域的九个位置坐标（每个位置的X轴坐标值和Y轴坐标值）。

2.双线性插值
(以下内容来自维基百科)

假如我们想得到未知函数 f 在点 P = (x, y) 的值，假设我们已知函数 f 在 Q11 = (x1, y1)、Q12 = (x1, y2), Q21 = (x2, y1) 以及 Q22 = (x2, y2) 四个点的值。最常见的情况，f就是一个像素点的像素值。首先在 x 方向进行线性插值，得到

然后在 y 方向进行线性插值，得到
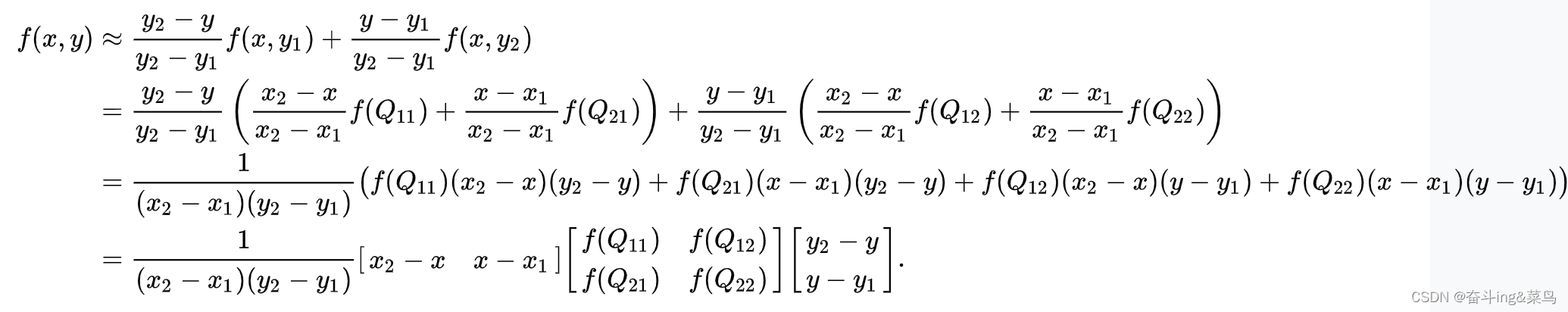对偏移后的采样点使用双线性插值计算获取每个采样点附近的特征信息。即计算与其周围4个最近邻像素之间的距离权重。对周围4个最近邻像素的像素值进行加权平均，得到偏移后位置处的像素值。

代码分析

import torch
from torch import nn


class DeformConv2d(nn.Module):
    def __init__(self, inc, outc, kernel_size=3, padding=1, stride=1, bias=None, modulation=False):
        """
        Args:
            modulation (bool, optional): If True, Modulated Defomable Convolution (Deformable ConvNets v2).
        """
        super(DeformConv2d, self).__init__()
        self.kernel_size = kernel_size
        self.padding = padding
        self.stride = stride
        self.zero_padding = nn.ZeroPad2d(padding)
        #可变形卷积
        self.conv = nn.Conv2d(inc, outc, kernel_size=kernel_size, stride=kernel_size, bias=bias)
				#求偏差值
        self.p_conv = nn.Conv2d(inc, 2*kernel_size*kernel_size, kernel_size=3, padding=1, stride=stride)
        nn.init.constant_(self.p_conv.weight, 0)
        self.p_conv.register_backward_hook(self._set_lr)

        self.modulation = modulation
        if modulation:
        #这个卷积层的作用在于计算出每个空间位置上的调制因子，该因子用于缩放特征图上不同空间位置的特征响应值，从而更好地适应不同形状、姿态的目标。
            self.m_conv = nn.Conv2d(inc, kernel_size*kernel_size, kernel_size=3, padding=1, stride=stride)
            nn.init.constant_(self.m_conv.weight, 0)
            self.m_conv.register_backward_hook(self._set_lr)

    @staticmethod
    #对梯度值进行缩放，减缓梯度更新的速度。该缩放操作可以帮助网络更平稳地收敛，避免梯度更新过快地跳出局部最优点。
    def _set_lr(module, grad_input, grad_output):
        grad_input = (grad_input[i] * 0.1 for i in range(len(grad_input)))
        grad_output = (grad_output[i] * 0.1 for i in range(len(grad_output)))
	#使用self.p_conv计算出偏移量offset，然后判断是否启用了调制（modulation），如果是，则通过self.m_conv计算出调制因子m，m的取值范围为[0, 1]，并在计算时使用sigmoid函数对输出进行映射。接下来根据偏移量和调制因子计算出各个采样点的位置，并进行采样操作。偏移量和调制因子都是可学习的，因此模型可以根据输入图像的不同区域自适应地学习到不同的偏移量和调制因子，从而更好地适应不同形状、姿态的目标。
    def forward(self, x):
        offset = self.p_conv(x)
        if self.modulation:
            m = torch.sigmoid(self.m_conv(x))

        dtype = offset.data.type()
        ks = self.kernel_size
        #表示在可变形卷积中，每个采样点的偏移量张量（offset）的通道数为N。在索引上，前N个通道表示x方向的偏移量，后N个通道表示y方向的偏移量。
        N = offset.size(1) // 2

        if self.padding:
            x = self.zero_padding(x)

        # (b, 2N, h, w)
        p = self._get_p(offset, dtype)

        # (b, h, w, 2N)
        p = p.contiguous().permute(0, 2, 3, 1)
        q_lt = p.detach().floor()
        q_rb = q_lt + 1

        q_lt = torch.cat([torch.clamp(q_lt[..., :N], 0, x.size(2)-1), torch.clamp(q_lt[..., N:], 0, x.size(3)-1)], dim=-1).long()
        q_rb = torch.cat([torch.clamp(q_rb[..., :N], 0, x.size(2)-1), torch.clamp(q_rb[..., N:], 0, x.size(3)-1)], dim=-1).long()
        q_lb = torch.cat([q_lt[..., :N], q_rb[..., N:]], dim=-1)
        q_rt = torch.cat([q_rb[..., :N], q_lt[..., N:]], dim=-1)

        # clip p
        p = torch.cat([torch.clamp(p[..., :N], 0, x.size(2)-1), torch.clamp(p[..., N:], 0, x.size(3)-1)], dim=-1)

        # bilinear kernel (b, h, w, N)
        g_lt = (1 + (q_lt[..., :N].type_as(p) - p[..., :N])) * (1 + (q_lt[..., N:].type_as(p) - p[..., N:]))
        g_rb = (1 - (q_rb[..., :N].type_as(p) - p[..., :N])) * (1 - (q_rb[..., N:].type_as(p) - p[..., N:]))
        g_lb = (1 + (q_lb[..., :N].type_as(p) - p[..., :N])) * (1 - (q_lb[..., N:].type_as(p) - p[..., N:]))
        g_rt = (1 - (q_rt[..., :N].type_as(p) - p[..., :N])) * (1 + (q_rt[..., N:].type_as(p) - p[..., N:]))

        # (b, c, h, w, N)
        x_q_lt = self._get_x_q(x, q_lt, N)
        x_q_rb = self._get_x_q(x, q_rb, N)
        x_q_lb = self._get_x_q(x, q_lb, N)
        x_q_rt = self._get_x_q(x, q_rt, N)

        # (b, c, h, w, N)
        x_offset = g_lt.unsqueeze(dim=1) * x_q_lt + \
                   g_rb.unsqueeze(dim=1) * x_q_rb + \
                   g_lb.unsqueeze(dim=1) * x_q_lb + \
                   g_rt.unsqueeze(dim=1) * x_q_rt

        # modulation
        if self.modulation:
            m = m.contiguous().permute(0, 2, 3, 1)
            m = m.unsqueeze(dim=1)
            m = torch.cat([m for _ in range(x_offset.size(1))], dim=1)
            x_offset *= m

        x_offset = self._reshape_x_offset(x_offset, ks)
        out = self.conv(x_offset)

        return out

    def _get_p_n(self, N, dtype):
        p_n_x, p_n_y = torch.meshgrid(
            torch.arange(-(self.kernel_size-1)//2, (self.kernel_size-1)//2+1),
            torch.arange(-(self.kernel_size-1)//2, (self.kernel_size-1)//2+1))
        # (2N, 1)
        p_n = torch.cat([torch.flatten(p_n_x), torch.flatten(p_n_y)], 0)
        p_n = p_n.view(1, 2*N, 1, 1).type(dtype)

        return p_n

    def _get_p_0(self, h, w, N, dtype):
        p_0_x, p_0_y = torch.meshgrid(
            torch.arange(1, h*self.stride+1, self.stride),
            torch.arange(1, w*self.stride+1, self.stride))
        p_0_x = torch.flatten(p_0_x).view(1, 1, h, w).repeat(1, N, 1, 1)
        p_0_y = torch.flatten(p_0_y).view(1, 1, h, w).repeat(1, N, 1, 1)
        p_0 = torch.cat([p_0_x, p_0_y], 1).type(dtype)

        return p_0

    def _get_p(self, offset, dtype):
        N, h, w = offset.size(1)//2, offset.size(2), offset.size(3)

        # (1, 2N, 1, 1)
        p_n = self._get_p_n(N, dtype)
        # (1, 2N, h, w)
        p_0 = self._get_p_0(h, w, N, dtype)
        p = p_0 + p_n + offset
        return p

    def _get_x_q(self, x, q, N):
        b, h, w, _ = q.size()
        padded_w = x.size(3)
        c = x.size(1)
        # (b, c, h*w)
        x = x.contiguous().view(b, c, -1)

        # (b, h, w, N)
        index = q[..., :N]*padded_w + q[..., N:]  # offset_x*w + offset_y
        # (b, c, h*w*N)
        index = index.contiguous().unsqueeze(dim=1).expand(-1, c, -1, -1, -1).contiguous().view(b, c, -1)

        x_offset = x.gather(dim=-1, index=index).contiguous().view(b, c, h, w, N)

        return x_offset

    @staticmethod
    def _reshape_x_offset(x_offset, ks):
        b, c, h, w, N = x_offset.size()
        x_offset = torch.cat([x_offset[..., s:s+ks].contiguous().view(b, c, h, w*ks) for s in range(0, N, ks)], dim=-1)
        x_offset = x_offset.contiguous().view(b, c, h*ks, w*ks)

        return x_offset
        
if __name__ == "__main__":
    input = torch.randn(1,3,224,224)
    model = DeformConv2d(3,64,3,1,1)
    out = model(input)
    print(out.shape)

喜欢的朋友可以关注我的公众号，搜索：啥也不是的AI技术栈
或者扫描下方的二维码：
感谢您的关注！！！