文章目录
0 前言
最近在学习贝叶斯网络，有些概念已经忘记了，索性就从头开始，将概率—>贝叶斯定理—>贝叶斯网络的公式和概念都串起来讲一遍。
1 概率公式
1.1 联合概率
联合概率指的是包含多个条件且所有条件同时成立的概率，记作P(X=a,Y=b)或P(A,B)，有的书上也习惯记作P(AB)。注意是所有条件同时成立，同时发生。
1.2 边缘概率(又称先验概率)
边缘概率是与联合概率对应的，P(X=a)或P(Y=b)，这类仅与单个随机变量有关的概率称为边缘概率
1.3 联合概率与边缘概率的关系
P
(
X
=
a
)
=
∑
b
P
(
X
=
a
,
Y
=
b
)
P
(
Y
=
b
)
=
∑
a
P
(
X
=
a
,
Y
=
b
)
\begin{aligned} &P(X=a)=\sum_b{P}(X=a,Y=b)\\ &P(Y=b)=\sum_a{P}(X=a,Y=b)\\ \end{aligned}
P(X=a)=b∑P(X=a,Y=b)P(Y=b)=a∑P(X=a,Y=b)
1.4 条件概率(又称先验概率)
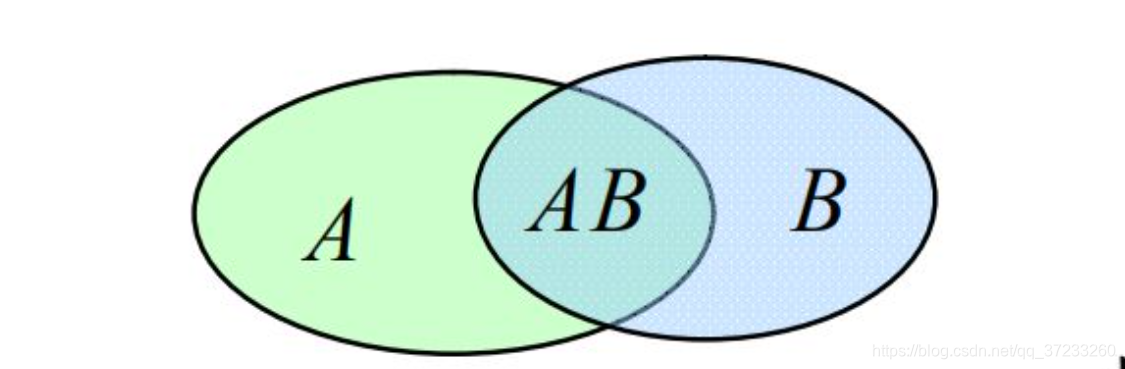
如图，
A
A
A和
B
B
B不是相互独立的，求在条件
B
B
B成立的情况下，
A
A
A的概率，记作
P
(
X
=
a
∣
Y
=
b
)
P(X=a|Y=b)
P(X=a∣Y=b)或
P
(
B
∣
A
)
P(B\mid A)
P(B∣A)，且有
P
(
B
∣
A
)
≠
P
(
B
)
P(B\mid A)\ne P(B)
P(B∣A)=P(B)。也就是
A
B
AB
AB中基本事件数占
A
A
A中的比例：
P
(
B
∣
A
)
=
P
(
A
B
)
P
(
A
)
P(B\mid A)=\frac{P(AB)}{P(A)}
P(B∣A)=P(A)P(AB)
1.5 全概率公式
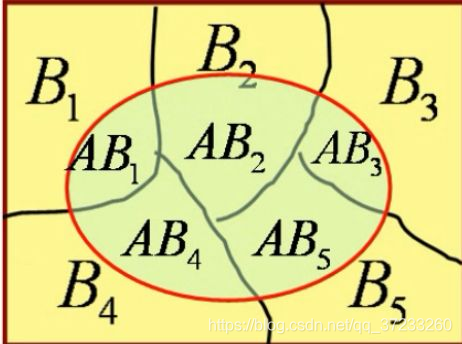
简单推导一下，如图：
P
(
A
)
=
P
(
A
B
1
)
+
P
(
A
B
2
)
+
P
(
A
B
3
)
+
P
(
A
B
4
)
+
P
(
A
B
5
)
P(A)=P\left( AB_1 \right) +P\left( AB_2 \right) +P\left( AB_3 \right) +P\left( AB_4 \right) +P\left( AB_5 \right)
P(A)=P(AB1)+P(AB2)+P(AB3)+P(AB4)+P(AB5)
由条件概率公式：
P
(
A
B
1
)
=
P
(
A
)
P
(
B
1
∣
A
)
=
P
(
B
)
P
(
A
∣
B
1
)
P\left( AB_1 \right) =P(A)P\left( B_1\mid A \right) =P(B)P\left( A\mid B_1 \right)
P(AB1)=P(A)P(B1∣A)=P(B)P(A∣B1)
代入可以得到：
P
(
A
)
=
P
(
A
)
P
(
B
1
A
)
+
P
(
A
)
P
(
B
2
∣
A
)
+
⋯
+
P
(
A
)
P
(
B
5
∣
A
)
=
P
(
B
1
)
P
(
A
∣
B
1
)
+
P
(
B
2
)
P
(
A
∣
B
2
)
+
⋯
+
P
(
B
5
)
P
(
A
∣
B
5
)
\begin{aligned} P(A)&=P(A)P\left( B_1A \right) +P(A)P\left( B_2\mid A \right) +\cdots +P(A)P\left( B_5\mid A \right)\\ &=P\left( B_1 \right) P\left( A\mid B_1 \right) +P\left( B_2 \right) P\left( A\mid B_2 \right) +\cdots +P\left( B_5 \right) P\left( A\mid B_5 \right)\\ \end{aligned}
P(A)=P(A)P(B1A)+P(A)P(B2∣A)+⋯+P(A)P(B5∣A)=P(B1)P(A∣B1)+P(B2)P(A∣B2)+⋯+P(B5)P(A∣B5)
简写为：
P
(
A
)
=
∑
i
P
(
A
∣
B
i
)
P
(
B
i
)
P(A)=\sum_i{P}\left( A\mid B_i \right) P\left( B_i \right)
P(A)=i∑P(A∣Bi)P(Bi)
2 贝叶斯公式
2.1 贝叶斯学派
讲解贝叶斯方法之前，先简单总结下频率派与贝叶斯派各自不同的思考方式：
- 频率派把需要推断的参数 θ θ θ看做是固定的未知常数，即概率 θ θ θ虽然是未知的，但最起码是确定的一个值，同时，样本 X X X是随机的，所以频率派重点研究样本空间，大部分的概率计算都是针对样本 X X X的分布；
- 而贝叶斯派的观点则截然相反，他们认为参数 θ θ θ是随机变量，而样本 X X X是固定的，由于样本是固定的，所以他们重点研究的是参数 θ θ θ的分布。
贝叶斯派既然把 θ θ θ看做是一个随机变量，所以要计算 θ θ θ的分布，便得事先知道 θ θ θ的无条件分布，即在有样本之前（或观察到X之前）， θ θ θ有着怎样的分布呢？比如往台球桌上扔一个球，这个球落会落在何处呢？如果是不偏不倚的把球抛出去，那么此球落在台球桌上的任一位置都有着相同的机会，即球落在台球桌上某一位置的概率服从均匀分布。这种在实验之前定下的属于基本前提性质的分布称为先验分布，或的无条件分布。
至此，贝叶斯及贝叶斯派提出了一个思考问题的固定模式：先验分布 p ( θ ) p(θ) p(θ)+ 样本信息 X X X⇒ 后验分布 p ( θ ∣ X ) p(θ|X) p(θ∣X)
上述思考模式意味着，新观察到的样本信息将修正人们以前对事物的认知。换言之，在得到新的样本信息之前，人们对的认知是先验分布 p ( θ ) p(θ) p(θ)，在得到新的样本信息后 X X X，人们对θ的认知为 p ( θ ∣ X ) p(θ|X) p(θ∣X)。而后验分布 p ( θ ∣ X ) p(θ|X) p(θ∣X)一般也认为是在给定样本 X X X的情况下 θ θ θ的条件分布，而使达到最大的值称为最大后验估计。
2.2 贝叶斯定理
此外，贝叶斯除了提出上述思考模式之外，还特别提出了贝叶斯定理。
考虑一个问题： P ( A ∣ B ) P(A|B) P(A∣B)是在B发生的情况下A发生的可能性。
首先，事件B发生之前，我们对事件A的发生有一个基本的概率判断，称为A的先验概率，用 P ( A ) P(A) P(A)表示；
其次，事件B发生之后，我们对事件A的发生概率重新评估，称为A的后验概率，用 P ( A ∣ B ) P(A|B) P(A∣B)表示；
类似的，事件A发生之前，我们对事件B的发生有一个基本的概率判断，称为B的先验概率，用 P ( B ) P(B) P(B)表示；
同样，事件A发生之后，我们对事件B的发生概率重新评估，称为B的后验概率，用 P ( B ∣ A ) P(B|A) P(B∣A)表示。
贝叶斯定理便是基于下述贝叶斯公式：
P
(
B
i
∣
A
)
=
P
(
A
∣
B
i
)
P
(
B
i
)
∑
j
P
(
A
∣
B
j
)
P
(
B
j
)
P\left( B_i\mid A \right) =\frac{P\left( A\mid B_i \right) P\left( B_i \right)}{\sum_j{P}\left( A\mid B_j \right) P\left( B_j \right)}
P(Bi∣A)=∑jP(A∣Bj)P(Bj)P(A∣Bi)P(Bi)
2.3 贝叶斯公式的应用
3 朴素贝叶斯算法
3.1 朴素贝叶斯的思想
朴素贝叶斯分类（NBC）是以贝叶斯定理为基础并且假设特征条件之间相互独立的方法，先通过已给定的训练集，以特征词之间独立作为前提假设，学习从输入到输出的联合概率分布，再基于学习到的模型，输入X求出使得后验概率最大的Y输出。
给定样本： X = { x 1 , x 2 , ⋯ , x d } X=\left\{ x_1,x_2,\cdots ,x_d \right\} X={x1,x2,⋯,xd}，有m个类： Y = { y 1 , y 2 , ⋯ , y m } Y=\left\{ y_1,y_2,\cdots ,y_m \right\} Y={y1,y2,⋯,ym}。给定 X X X，计算最大的概率 P ( Y = y i ∣ X ) P\left( Y=y_i\mid X \right) P(Y=yi∣X)。
将全概率公式代入贝叶斯公式，写成贝叶斯公式的一般形式（也可以由条件概率来推）：
P ( Y = y i ∣ X ) = P ( X ∣ Y = y i ) P ( Y = y i ) P ( X ) P\left( Y=y_i\mid X \right) =\frac{P\left( X\mid Y=y_i \right) P\left( Y=y_i \right)}{P(X)} P(Y=yi∣X)=P(X)P(X∣Y=yi)P(Y=yi)
由朴素贝叶斯算法可得，后验概率 P ( Y ∣ X ) P\left( Y\mid X \right) P(Y∣X)可以由先验概率 P ( Y ) P(Y) P(Y) 、证据P(X) 、类条件概率 P ( X ∣ Y ) P\left( X\mid Y \right) P(X∣Y)计算出。
3.2 朴素贝叶斯分类器
给定 X X X，要求出其类别 Y Y Y，朴素贝叶斯分类器的目标函数为：
y ^ = a r g max P ( Y ∣ X ) = max P ( X ∣ Y ) P ( Y ) P ( X ) \hat{y}=arg\max P\left( Y\mid X \right) =\max \frac{P\left( X\mid Y \right) P\left( Y \right)}{P(X)} y^=argmaxP(Y∣X)=maxP(X)P(X∣Y)P(Y)
因为对于
P
(
X
)
P(X)
P(X)对于所有类都是常数，原式子可以写为（已知先验概率的情况，先验概率可以用极大似然估计来求）：
y
^
=
a
r
g
max
P
(
Y
∣
X
)
=
max
P
(
X
∣
Y
)
P
(
Y
)
\hat{y}=arg \max P\left( Y\mid X \right) =\max P\left(X \mid Y \right) P(Y)
y^=argmaxP(Y∣X)=maxP(X∣Y)P(Y)
另一种写法（等价的）：
y
^
=
arg
max
y
P
(
y
)
∏
i
=
1
n
P
(
x
i
∣
y
)
\hat{y}=\underset{y}{\arg \max } P(y) \prod_{i=1}^{n} P\left(x_{i} \mid y\right)
y^=yargmaxP(y)i=1∏nP(xi∣y)
进一步，且若在先验概率
P
(
Y
=
y
)
P(Y=y)
P(Y=y)假设是相等的情况下，原式子可以写为：
y
^
=
a
r
g
max
P
(
Y
∣
X
)
=
max
P
(
X
∣
Y
)
\hat{y}=arg \max P\left( Y\mid X \right) =\max P\left(X \mid Y \right)
y^=argmaxP(Y∣X)=maxP(X∣Y)
Tip1：实际计算中，会将
Y
Y
Y的值从
y
0
y_0
y0到
y
i
y_i
yi遍历一遍然后相乘，但是结果算出来并不是概率值，只是取最大的那个值对应的类别认为是输入
X
X
X的类别。
Tip2：如果样本太少，可以假定某种分布，比如都是正态分布：
P
(
x
i
∣
y
)
=
1
2
π
σ
y
exp
(
−
(
x
i
−
μ
y
)
2
2
σ
y
2
)
P\left(x_{i} \mid y\right)=\frac{1}{\sqrt{2 \pi} \sigma_{y}} \exp \left(-\frac{\left(x_{i}-\mu_{y}\right)^{2}}{2 \sigma_{y}^{2}}\right)
P(xi∣y)=2πσy1exp(−2σy2(xi−μy)2)通过样本计算出均值和方差，也就是得到正态分布的密度函数。有了密度函数，就可以把值代入，算出某一点的密度函数的值。
Tip3：朴素贝叶斯的条件独立假设很难保证，实际能用就行。
4 贝叶斯网络
朴素贝叶斯可以认为是一种特殊的贝叶斯网络，只是所有条件都是独立的，而通常会把某个研究系统中涉及的随机变量, 根据是否条件独立绘制在一个有向图中, 就形成了贝叶斯网络。贝叶斯网络(Bayesian Network), 又称有向无环图模 型 (directed acyclic graphical model,DAG), 是一种概率图模型, 根据概率图的拓扑结构, 考察一组随机变量 { X 1 , X 2 … X n } \left\{\mathrm{X}_{1},\mathrm{X}_{2}\ldots\mathrm{X}_{\mathrm{n}}\right\} {X1,X2…Xn} 及其n组条件概率分布(Conditional Probability Distributions, CPD) 的性质。
4.1 贝叶斯网络的三种基础模型
4.2 全连接的贝叶斯网络
每一对结点之间都有边连接。
其联合概率为：
p
(
a
,
b
,
c
)
=
p
(
c
∣
a
,
b
)
p
(
b
∣
a
)
p
(
a
)
p(a,b,c)=p(c\mid a,b)p(b\mid a)p(a)
p(a,b,c)=p(c∣a,b)p(b∣a)p(a)
对于全连接贝叶斯网络的联合概率的通用表达形式：
p ( x 1 , . . . , x K ) = p ( x K ∣ x 1 , . . . , x K − 1 ) . . . p ( x 2 ∣ x 1 ) p ( x 1 ) = ∏ K p ( X i = x i ∣ X i + 1 = x i + 1 , . . . , X K = x K ) \begin{aligned} &p\left( x_1,...,x_K \right) =p\left( x_K\mid x_1,...,x_{K-1} \right) ...p\left( x_2\mid x_1 \right) p\left( x_1 \right)\\ &=\prod_K{p}\left( X_i=x_i\mid X_{i+1}=x_{i+1},...,X_K=x_K \right)\\ \end{aligned} p(x1,...,xK)=p(xK∣x1,...,xK−1)...p(x2∣x1)p(x1)=K∏p(Xi=xi∣Xi+1=xi+1,...,XK=xK)
4.3 一般的贝叶斯网络
一般的贝叶斯网络可以有部分边缺失，而且直观上通过前部分的独立性判断可以知道：1. x 1 x_1 x1和 x 2 x_2 x2独立； 2. x 6 x_6 x6和 x 7 x_7 x7在 x 4 x_4 x4给定的条件下独立。
其联合概率为：
p
(
x
1
)
p
(
x
2
)
p
(
x
3
)
p
(
x
4
∣
x
1
,
x
2
,
x
3
)
p
(
x
5
∣
x
1
,
x
3
)
p
(
x
6
∣
x
4
)
p
(
x
7
∣
x
4
,
x
5
)
p\left(x_{1}\right) p\left(x_{2}\right) p\left(x_{3}\right) p\left(x_{4} \mid x_{1}, x_{2}, x_{3}\right) p\left(x_{5} \mid x_{1}, x_{3}\right) p\left(x_{6} \mid x_{4}\right) p\left(x_{7} \mid x_{4}, x_{5}\right)
p(x1)p(x2)p(x3)p(x4∣x1,x2,x3)p(x5∣x1,x3)p(x6∣x4)p(x7∣x4,x5)
小结：计算联合概率，就是求每个变量的条件概率，因为这里很多都不是独立的，所以每个“果”之前要找到“因”。这两个因果不是真的因果，表征两者是关联的，不是独立的，或许存在一些隐变量。
4.4 贝叶斯网络应用
通过贝叶斯网络计算John和Mary同时告诉这个事情，且铃声也响起了，但没有外族入侵也没有地震的概率有多大？
P
(
j
,
m
,
a
,
b
ˉ
,
e
ˉ
)
=
P
(
j
∣
a
)
P
(
m
∣
a
)
P
(
a
∣
b
ˉ
,
e
ˉ
)
P
(
b
ˉ
)
P
(
e
ˉ
)
=
0.9
×
0.7
×
0.001
×
0.999
×
0.998
≈
0.00063
\begin{aligned} &P(j, m, a, \bar{b}, \bar{e}) \\ &=P(j \mid a) P(m \mid a) P(a \mid \bar{b}, \bar{e}) P(\bar{b}) P(\bar{e}) \\ &=0.9 \times 0.7 \times 0.001 \times 0.999 \times 0.998 \\ &\approx 0.00063 \end{aligned}
P(j,m,a,bˉ,eˉ)=P(j∣a)P(m∣a)P(a∣bˉ,eˉ)P(bˉ)P(eˉ)=0.9×0.7×0.001×0.999×0.998≈0.00063
4.5 总结
通过给定的样本数据，建立贝叶斯网络的拓扑结构和结点的条件概率分布参数。往往需要借助先验知识和极大似然估计来完成。在上述两个确定的前提下，可以使用该网络，对未知数据计算条件概率，从而达到预测或者分类的目的。
9009
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
