第一，二类斯特林数 Bell数 Stirling公式

斯特林数是组合数学的内容。

第一类斯特林数可以处理下面的问题：把N个不同元素分为k个环，每个环非空，问有多少分法，记为S（p，k），

S(p,p)=1

S(p,0)=0

递推公式为：S(p,k)=(p-1)*S(p-1,k)+S(p-1.k-1)。

p个人排k个圈，第一种方法是，第k个圈只有p自己，所以加上S(p-1,k-1)，还有一种方法是p加入p-1人组成的k个圈，排在任意一个人的左边，加上(p-1)*S(p-1,k)。

第二类斯特林数可以解决下面的问题：把N个元素分为K个集合，每个盒子非空，问有多少方法，即为S(p,k)

S(p,p)=1

S(p,0)=0

S(p,k)=k*S(p-1,k)+S(p-1,k-1)

有两种分法。

1：让p在单独的一个集合里，S(p-1,k-1)

2：让p和其他元素在一个盒子里，k*S(p-1,k);

Bell数：记为B(p)将p个元素分到非空且相同的若干个盒子里。

贝尔数适合递推公式：

它们也适合“Dobinski公式”：

期望值为1的 泊松分布的''n''次 矩。

它们也适合“Touchard同余”：若p是任意 质数，那么

Stirling数S（n, k）是把基数为n的集划分为正好k个非空集的方法的数目。

把任一 概率分布的n次矩以首n个累积量表示的 多项式，其 系数和正是第n个贝尔数。这种数划分的方法不像用Stirling数那个方法粗糙。

贝尔数的指数 母函数是

B0= B1=1

B(p)=S(p,0)+S(p,1)+.....+S(p,k)   （S为第二类斯特林数）

Stirling公式可以用来求n！的近似值。

  

如果要计算N！为几位数，则我们可以用公式：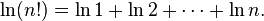

而我们同样可以用斯特林公式取lg计算。