视觉SLAM理论到实践系列（二）——三维物体的刚体运动（2）

视觉SLAM理论到实践系列

视觉SLAM理论到实践系列（一）——SLAM概述与预备知识

视觉SLAM理论到实践系列（二）——三维物体的刚体运动（1）

视觉SLAM理论到实践系列（二）——三维物体的刚体运动（2）

下面是《视觉SLAM十四讲》学习笔记的系列记录的总链接，本人发表这个系列的文章链接均收录于此

视觉SLAM理论到实践系列文章链接

---

下面是专栏地址：

视觉SLAM理论到实践专栏

---

---

前言

高翔博士的《视觉SLAM14讲》学习笔记的系列记录

---

视觉SLAM理论到实践系列（二）——三维物体的刚体运动（2）

Eigen使用

Eign中对各种形式的表达方式总结如下。请注意每种类型都有单精度和双精度两种数据类型，而且和之前一样，不能由编译器自动转换。下面以双精度为例，你可以把最后的 d 改成 f ，即得到单精度的数据结构。

• 旋转矩阵（3×3)：Eigen:Matrix.3d。
• 旋转向量(3×1)：Eigen:AngleAxisd。
• 欧拉角（3×1)：Eigen:Vector3d。
• 四元数(4×1)：Eigen:Quaterniond
• 欧氏变换矩阵(4×4)：Eigen:Isometry3d。
• 仿射变换(4×4)：Eigen:Affine3d。
• 射影变换(4×4)：Eigen:Projective.3d。

参考代码中对应的CMakeLists即可编译此程序。在这个程序中，演示了如何使用Eigen中的旋转矩阵、旋转向量、欧拉角和四元数。我们用这几种旋转方式旋转一个向量 $v$ ，发现结果是一样的。

同时，也演示了如何在程序中转换这几种表达方式。想进一步了解Eigen的几何模块的读者可以参考(http://eigen.tuxfamily.org/dox/group__TutorialGeometry.html)

Eigen官网：http://eigen.tuxfamily.org

这里使用高翔的slambook的源码，这里的源码采用嵌套式的CMakeLists.txt结构，即最外面的CMakeLists.txt包面里面的子文件夹

建立一个build目录，然后对源码进行编译

编译完成后产生的可执行二进制文件都在build目录下

coordinateTransform 执行结果

eigenMatrix执行结果

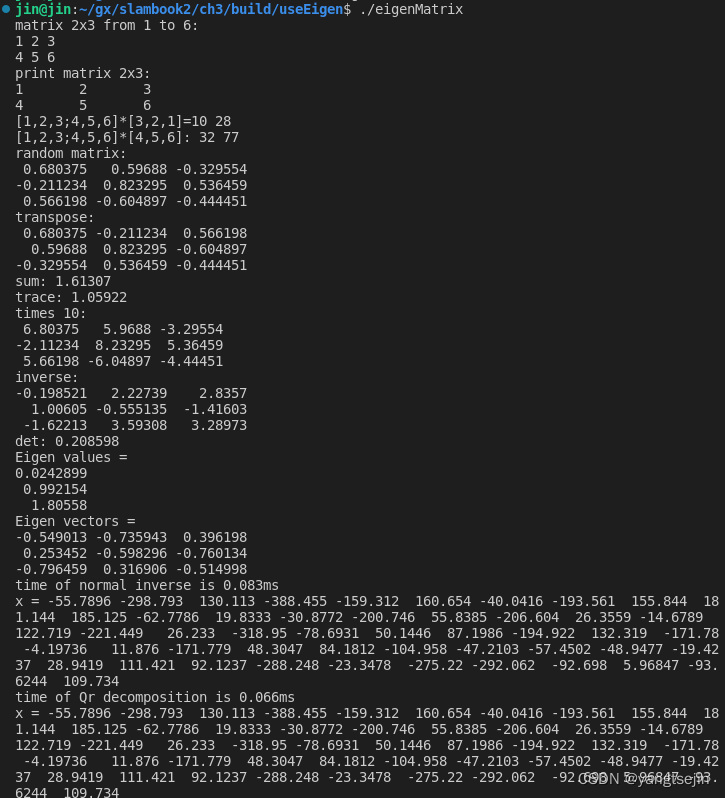
eigenGeometry执行结果

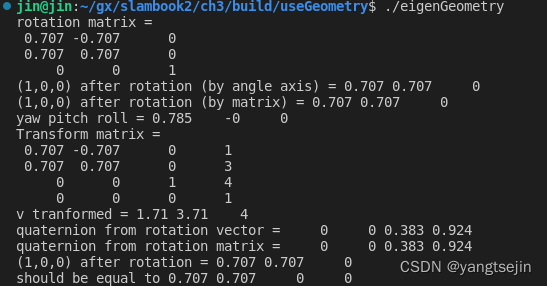
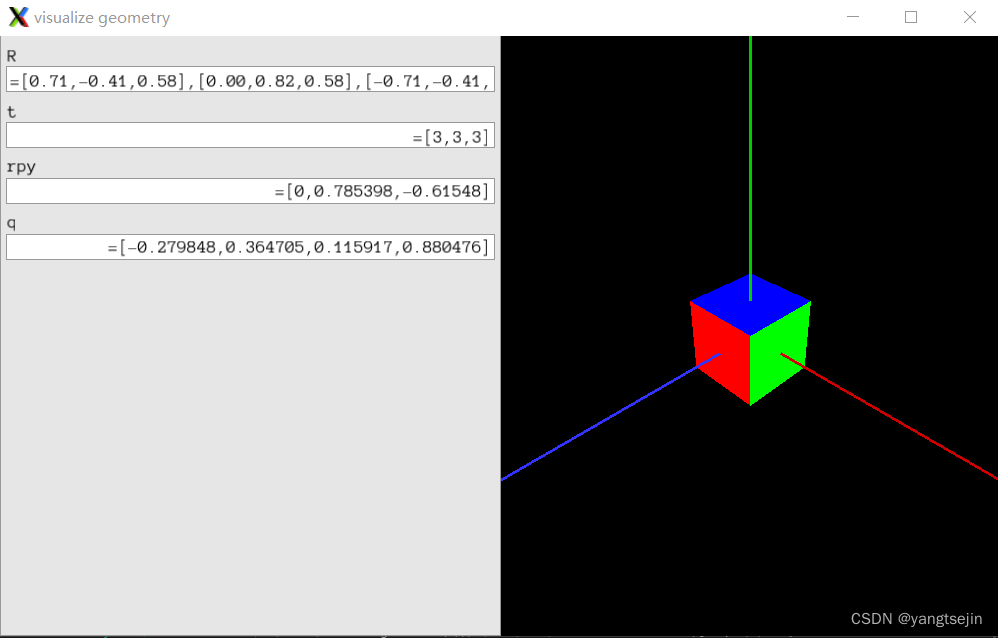
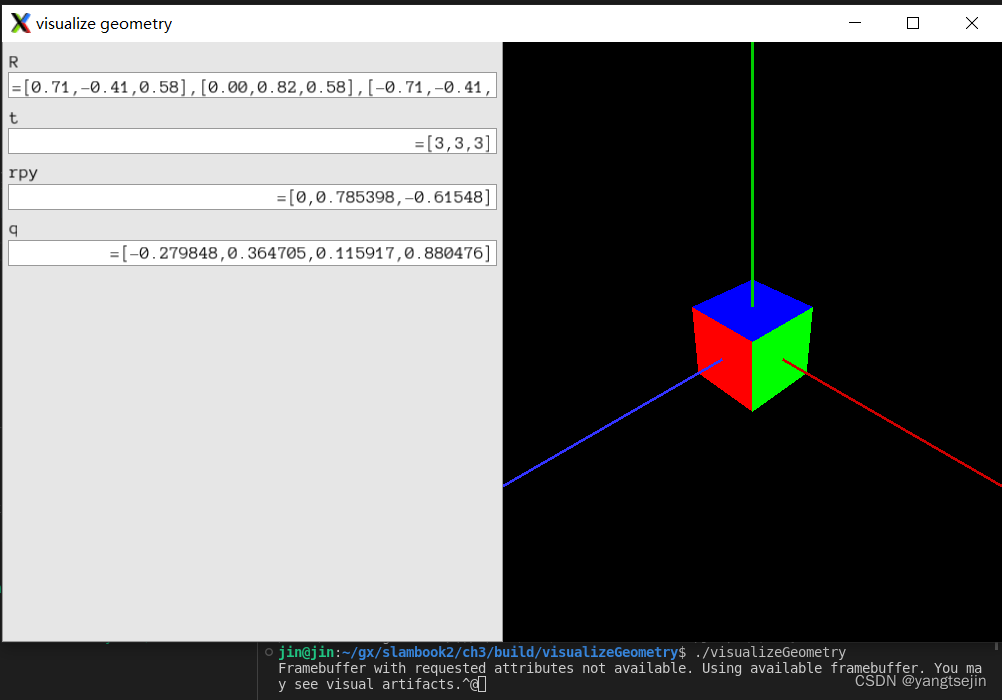
visualizeGeometry执行结果

出现的错误

错误1

在编译slambook的ch3的源码时，会报如下错误

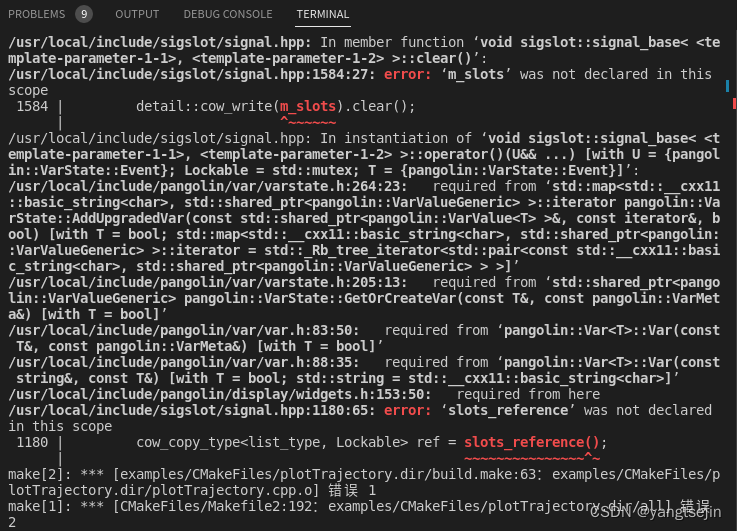
其实是 C++ 11 不支持编译，把 CMakeLists.txt中的C++版本换到 C++14 就可以了

sed -i 's/++11/++14/g' CMakeLists.txt

但这里源码中的CMakeLists.txt没有指定编译的C++版本，所以在编译时指定c++的版本

cmake CMakeLists.txt文件路径 -DCMAKE_CXX_STANDARD=14

即

cd build
cmake .. -DCMAKE_CXX_STANDARD=14

即可编译成功

错误2

参考：

error while loading shared libraries的解决方案

SLAM第三讲实践报错：./visualizeGeometry: error while loading shared libraries:报错

visualizeGeometry执行时报错

找不到动态库libpango_windowing.so

解决方法：

更改配置文件

1. 一般安装目录在：
   /usr/local/lib
   配置文件在：/etc/ld.so.conf文件中
   将该目录加入到共享库的配置文件中
2. 将动态库文件加入配置：执行vi /etc/ld.so.conf，在"include ld.so.conf.d/*.conf"下方增加"/usr/local/lib"。
3. 保存后，在命令行终端执行：
   /sbin/ldconfig -v
ldconfig
   其作用是将文件/etc/ld.so.conf列出的路径下的库文件缓存到/etc/ld.so.cache以供使用，因此当安装完一些库文件，或者修改/etc/ld.so.conf增加了库的新搜索路径，需要运行一下ldconfig，使所有的库文件都被缓存到文件/etc/ld.so.cache中，如果没做，可能会找不到刚安装的库。

经过以上三个步骤，"error while loading shared libraries"的问题通常情况下就可以解决了。

输入命令

sudo ldconfig

然后再执行即可

矩阵运算

详见：Matrix calculus

第二章习题

熟悉 Eigen 矩阵运算 (3 分，约 2 小时)

Eigen（http://eigen.tuxfamily.org）是常用的 C++ 矩阵运算库，具有很高的运算效率。大部分需要在 C++ 中使用矩阵运算的库，都会选⽤ Eigen 作为基本代数库，例如 Google Tensorflow，Google Ceres，GTSAM等。本次习题，你需要使⽤ Eigen 库，编写程序，求解⼀个线性⽅程组。为此，你需要先了解⼀些有关线性方程组数值解法的原理。

设线性⽅程 $Ax=b$，在 $A$ 为方阵的前提下，请回答以下问题：

1. 在什么条件下，$x$ 有解且唯⼀？

2. 高斯消元法的原理是什么？

3. QR 分解的原理是什么？

4. Cholesky 分解的原理是什么？

5. 编程实现 $A$ 为 100 × 100 随机矩阵时，用 QR 和 Cholesky 分解求 $x$ 的程序。你可以参考本次课用到的 useEigen 例程。

提示：你可能需要参考相关的数学书籍或文章。请善用搜索引擎。Eigen 固定大小矩阵最支持到 50，所以你会用到动态大小的矩阵

解答

参考：

视觉SLAM十四讲（第二章作业）

视觉SLAM理论与实践学习笔记（二）

有关旋转矩的证明

（1）当 $R(A)=R(A|B)$ 时方程组有解，当 $R(A)=R(A,B)=n$（n为未知数个数）时方程组有唯一解

矩阵 $A$ 满秩时有唯一解，$A$ 满秩的判断条件为 $|A|\ne 0$

（2）高斯消元法是线性代数中的一种算法，可用于求解线性方程组的解，以及求出矩阵的秩，和求出可逆矩阵的逆矩阵。高斯消元法的原理是：通过用初等行变换将增广矩阵化为行阶梯阵，然后通过回带求解线性方程组的解。

若用初等行变换将增广矩阵 $(AB)$ 化为 $(CD)$ ，则AX = B与CX = D是同解方程组。

所以我们可以用初等行变换把增广矩阵转换为行阶梯阵，然后回代求出方程的解

参考：高斯消元原理

（3）QR分解

注意：这里被分解矩阵A不一定是方阵，也可以是非方阵。Q为正交矩阵，R为上三角矩阵。

（4）矩阵分解 Cholesky分解

注意：这里被分解的矩阵A必须是对称正定阵，L为下三角矩阵。

（5）QR分解和Cholesky分解的代码如下

根目录CMakeLists.txt

cmake_minimum_required(VERSION 2.8)
project(decomp)

set(EXEC_PATH ${CMAKE_CURRENT_SOURCE_DIR}/bin)

# add subdir
add_subdirectory(cholesky)
add_subdirectory(qr)

QR分解CMakeLists.txt

cmake_minimum_required(VERSION 2.8)
project(qrdecomp)

set(CMAKE_BUILD_TYPE "Release")
set(CMAKE_CXX_FLAGS "-O3")
set(EXECUTABLE_OUTPUT_PATH ${EXEC_PATH})

include_directories(/usr/include/eigen3)
# include_directories(/usr/local/include/)

add_executable(qrdecomp qr_decomp.cpp)

代码如下

#include<iostream>
#include<Eigen/Dense>
#include<cmath>
#define MATRIX_SIZE 100

int main(int argc, char const *argv[])
{
    // to solve Ax=b,where A is 100*100 matrix,b is 100*1 vector
    Eigen::MatrixXd A=Eigen::MatrixXd::Random(MATRIX_SIZE,MATRIX_SIZE);
    A=A*A.transpose();  // 保证半正定
    Eigen::MatrixXd b=Eigen::MatrixXd::Random(MATRIX_SIZE,1);
    std::cout <<"Matrix A :\n"<< A << std::endl;
    std::cout<<"Vector b:\n"<<b<<std::endl;

    Eigen::MatrixXd x;
    x=A.colPivHouseholderQr().solve(b);

    std::cout<<"x="<<x.transpose()<<std::endl;

    return 0;
}

Cholesky分解CMakeLists.txt

cmake_minimum_required(VERSION 2.8)
project(cholesky)

set(CMAKE_BUILD_TYPE "Release")
set(CMAKE_CXX_FLAGS "-O3")
set(EXECUTABLE_OUTPUT_PATH ${EXEC_PATH})

include_directories(/usr/include/eigen3)
# include_directories(/usr/local/include/)

add_executable(cholesky cholesky_decomposition.cpp)

代码如下

#include<iostream>
#include<Eigen/Dense>
#include<cmath>

#define MATRIX_SIZE 100

int main(int argc, char const *argv[])
{
    Eigen::MatrixXd A=Eigen::MatrixXd::Random(MATRIX_SIZE,MATRIX_SIZE);
    Eigen::MatrixXd b=Eigen::MatrixXd::Random(MATRIX_SIZE,1);
    A=A*A.transpose();

    Eigen::MatrixXd x;
    x=A.ldlt().solve(b);

    std::cout<<"x = \n"<<x.transpose()<<std::endl;
    return 0;
}

几何运算练习 (2 分，约 1 小时)

下面我们来练习如何使⽤ Eigen/Geometry 计算⼀个具体的例子。

设有小萝卜1⼀号和小萝卜二号位于世界坐标系中。小萝卜一号的位姿为：$q_1=[0.55,0.3,0.2,0.2],t1=[0.7,1.1,0.2{]}^T$（$q$ 的第⼀项为实部）。这⾥的 $q$ 和 $t$ 表达的是 $T_{cw}$，也就是世界到相机的变换关系。小萝卜二号的位姿为 $q_2=[-0.1,0.3,-0.7,0.2],t_2=[-0.1,0.4,0.8{]}^T$。现在，小萝卜一号看到某个点在自身的坐标系下，坐标为 $p_1=[0.5,-0.1,0.2{]}^T$，求该向量在小萝卜二号坐标系下的坐标。请编程实现此事，并提交你的程序。

提示：

1. 四元数在使用前需要归⼀化。

2. 请注意 Eigen 在使用四元数时的虚部和实部顺序。

3. 参考答案为 $p_2=[1.08228,0.663509,0.686957{]}^T$。你可以用它验证程序是否正确。

解答

参考：

视觉SLAM十四讲中P61作业7。

高博课程编程作业之计算小萝卜的坐标

（1）用四元数的方法计算

整体思路是由 $p_1，q_1,t_1$ 计算点在世界坐标下的坐标 $p_w$

先把四元数归一化，题目给出的表达是 $T_{cw}$,是世界到相机的变换关系，所以要先把 $q_1$ 转化为相机到世界的变换，也就是 $q_1$ 的逆可以表达相反的变换

对于单位四元数，其逆和共轭就是同一个量，而四元数的共轭是把虚部取成相反数，所以在归一化的时候把 $q_1$ 的虚部取为相反数就行了。
$$p_w=q_1\ast (p_1-t_1)$$
然后计算 $p_w$ 在萝卜二号坐标系的坐标
$$p_2=p_w\ast q_2+t_2$$
代入如下

//本程序用来求解位姿变换问题
#include <iostream>
#include <cmath>
#include <Eigen/Core>
#include <Eigen/Dense>
// Eigen 几何模块
#include <Eigen/Geometry>

int main( int argc, char** argv)
{
  Eigen::Vector3d p1,t1,t2;
  p1 << 0.5,-0.1,0.2;
  t1 << 0.7,1.1,0.2;
  t2 << -0.1,0.4,0.8;
// 四元数Eigen::Quaterniond 的正确初始化顺序为Eigen::Quaterniond(w,x,y,z)
// 而 coeffs的顺序是（x,y,z,w）,w 为实部，前三者为虚部
// 因为要表示相反的旋转，故输入为q1的共轭，即实部不变，虚部变为相反数
  Eigen::Quaterniond q1 = Eigen::Quaterniond(0.55,-0.3,-0.2,-0.2).normalized();
  std::cout << "q1 coeffs is \n"<<q1.coeffs().transpose() << std::endl;


  Eigen::Quaterniond q2 = Eigen::Quaterniond(-0.1,0.3,-0.7,0.2).normalized();
  std::cout << "q2 coeffs is \n"<<q2.coeffs().transpose() << std::endl;

  Eigen::Vector3d pw = q1*(p1-t1);  //数学上是qpq-1
  Eigen::Vector3d p2 = q2*pw + t2;

  std::cout << p2.transpose() << std::endl;

  return 0;
}

（2）用变换矩阵的方法

同样的思路，先求出两个变换矩阵 $T_1$ 和 $T_2$ ，$p_1$ 和 $T_1$ 的逆矩阵相乘得到 $p_w$, 然后再和 $T_2$ 相乘得到 $p_2$
$$p_2=T_2\ast T_1^{-1}\ast p_1$$
代码如下

#include<iostream>
#include<Eigen/Dense>
#include<Eigen/Geometry>

int main ( int argc, char** argv )
{
  Eigen::Quaternion<double> q1(0.55,0.3, 0.2, 0.2 );//小萝卜1号坐标相对于世界坐标的四元数
  Eigen::Quaternion<double> q2(-0.1,0.3, -0.7, 0.2);//小萝卜2号坐标相对于世界坐标的四元数
  q1.normalize();//四元数归一化
  q2.normalize();//四元数归一化
  
  Eigen::Vector3d t1(0.7, 1.1, 0.2);//小萝卜1号坐标相对于世界坐标的平移向量
  Eigen::Vector3d t2(-0.1, 0.4, 0.8);//小萝卜2号坐标相对于世界坐标的平移向量
  
  Eigen::Matrix3d R1 = q1.toRotationMatrix();//小萝卜1号的四元数 转为 旋转矩阵
  Eigen::Matrix3d R2 = q2.toRotationMatrix();//小萝卜2号的四元数 转为 旋转矩阵
  
  Eigen::Isometry3d Tcw1(R1);//创建小萝卜1号相对于世界坐标的欧氏变换矩阵，并用旋转矩阵 初始化  
  Eigen::Isometry3d Tcw2(R2);//创建小萝卜2号相对于世界坐标的欧氏变换矩阵，并用旋转矩阵 初始化   
  Tcw1.pretranslate(t1);//接着，用平移向量初始化小萝卜1号的欧氏变换矩阵
  Tcw2.pretranslate(t2);//接着，用平移向量初始化小萝卜2号的欧氏变换矩阵
  
  Eigen::Vector3d p1(0.5, -0.1, 0.2);//点d在小萝卜1号坐标下的向量表示
  Eigen::Vector3d pd_w = Tcw1.inverse() * p1;//算出点d在世界坐标下的向量表示，其中，Tcw表示world to camera 的坐标变换，Tcw.inverse表示camera to world的变换
  Eigen::Vector3d p2 = Tcw2 * pd_w;//算出点d在小萝卜2号的向量表示
  
  std::cout << p2.transpose() << std::endl;
  
  return 0;
}

CMakeLists.txt如下

cmake_minimum_required(VERSION 2.8)
project(geo_calc)

include_directories("/usr/include/eigen3")
set(EXEC_PATH ${CMAKE_CURRENT_SOURCE_DIR}/bin)
set(EXECUTABLE_OUTPUT_PATH ${EXEC_PATH})
add_executable(geo geo_calc.cpp)

结果如下

旋转的表达 （2 分，约 1 小时）

课程中提到了旋转可以用旋转矩阵、旋转向量与四元数表达，其中旋转矩阵与四元数是日常应用中常见的表达方式。请根据课件知识，完成下述内容的证明。

1. 设有旋转矩阵 $R$，证明 $R^{T}R=I$ 且 det $R$ = +1¹。

2. 设有四元数 $q$，我们把虚部记为 $\epsilon$，实部记为 $\eta$，那么 $q=(\epsilon ,\eta )$。请说明 $\epsilon$ 和 $\eta$ 的维度。

3. 定义运算 + 和 ⊕ 为：
   $$q^{+}=\left[\begin{array}{cc}\eta 1-{\epsilon }^{\times }& \epsilon \\ -{\epsilon }^{\mathrm{T}}& \eta \end{array}\right],q^{\oplus }=\left[\begin{array}{cc}\eta 1+{\epsilon }^{\times }& \epsilon \\ -{\epsilon }^{\mathrm{T}}& \eta \end{array}\right],\text{\hspace{1em}(1)}$$
   其中运算 ${}^{\times }$ 含义与 ${}^{\wedge }$ 相同，即取 ε 的反对称矩阵（它们都成叉积的矩阵运算形式），$1$ 为单位矩阵

   请证明对任意单位四元数 $q_1,q_2$，四元数乘法可写成矩阵乘法：
   $$q_1\cdot q_2=q_1^{+}{q}_2\text{\hspace{1em}(2)}$$
   或者
   $$q_1\cdot q_2=q_2^{\oplus }{q}_1.\text{\hspace{1em}(3)}$$

解答

（1）设有两组正交基 $(e_1,e_2,e_3)$ 和 $(e_1^{\prime },e_2^{\prime },e_3^{\prime })$ ，以及在这两组正交基下的坐标 $a=(a_1,a_2,a_3)$ 与 $a^{\prime }=(a_1^{\prime },a_2^{\prime },a_3^{\prime })$

根据坐标系的定义
$$[{\mathbf{e}}_1,{\mathbf{e}}_2,{\mathbf{e}}_3]\left[\begin{array}{c}{\mathbf{a}}_1\\ {\mathbf{a}}_2\\ {\mathbf{a}}_3\end{array}\right]=[{\mathbf{e}}_1^{\prime },{\mathbf{e}}_2^{\prime },{\mathbf{e}}_3^{\prime }]\left[\begin{array}{c}{\mathbf{a}}_1^{\prime }\\ {\mathbf{a}}_2^{\prime }\\ {\mathbf{a}}_3^{\prime }\end{array}\right]$$
则
$$\left[\begin{array}{c}{\mathbf{a}}_1\\ {\mathbf{a}}_2\\ {\mathbf{a}}_3\end{array}\right]=\left[\begin{array}{ccc}{\mathbf{c}}_1^{\mathbf{T}}{\mathbf{e}}_1^{\prime \prime }& {\mathbf{e}}_1^{\mathbf{T}}{\mathbf{e}}_2^{\prime \prime }& {\mathbf{e}}_1^{\mathbf{T}}{\mathbf{e}}_3^{\prime \prime }\\ {\mathbf{e}}_2^{\mathbf{T}}{\mathbf{e}}_1^{\prime \prime }& {\mathbf{e}}_2^{\mathbf{T}}{\mathbf{e}}_2^{\prime \prime }& {\mathbf{e}}_2^{\mathbf{T}}{\mathbf{e}}_3^{\prime \prime }\\ {\mathbf{e}}_3^{\mathbf{T}}{\mathbf{e}}_1^{\prime \prime }& {\mathbf{e}}_3^{\mathbf{T}}{\mathbf{e}}_2^{\prime \prime }& {\mathbf{e}}_3^{\mathbf{T}}{\mathbf{e}}_3^{\prime \prime }\end{array}\right]\left[\begin{array}{c}{\mathbf{a}}_1^{\prime \prime }\\ {\mathbf{a}}_2^{\prime \prime }\\ {\mathbf{a}}_2^{\prime \prime }\end{array}\right]=\mathrm{R}{\mathrm{a}}^{\prime }\text{\hspace{1em}(1)}$$
其中 $R$ 为旋转矩阵，$R^{T}R$ 为：
$${\mathrm{R}}^T\mathrm{R}=\left[\begin{array}{ccc}{e}_1^T{e}_1^{\prime }& e_2^T{e}_1^{\prime }& e_3^T{e}_1^{\prime }\\ e_1^T{e}_2^{\prime }& e_2^T{e}_2^{\prime }& e_3^T{e}_2^{\prime }\\ e_1^T{e}_3^{\prime }& e_2^T{e}_3^{\prime }& e_3^T{e}_3^{\prime }\end{array}\right]\left[\begin{array}{ccc}{c}_1^T{e}_1^{\prime }& e_1^T{e}_2^{\prime }& e_1^T{e}_3^{\prime }\\ e_2^T{e}_1& e_2^T{e}_2^{\prime }& e_2^T{e}_3^{\prime }\\ e_3^T{e}_1^{\prime }& e_3^T{e}_2^{\prime }& e_3^T{e}_3^{\prime }\end{array}\right]=I\text{\hspace{1em}(2)}$$
其中
$$\begin{array}{rl}& \left({\mathrm{e}}_1^{\mathrm{T}}{\mathrm{e}}_1^{\prime }\right)\times \left({\mathrm{e}}_1^{\mathrm{T}}{\mathrm{e}}_1^{\prime }\right)+\left({\mathrm{e}}_2^{\mathrm{T}}{\mathrm{e}}_1^{\prime }\right)\times \left({\mathrm{e}}_2^{\mathrm{T}}{\mathrm{e}}_1^{\prime }\right)+\left({\mathrm{e}}_3^{\mathrm{T}}{\mathrm{e}}_1^{\prime }\right)\times \left({\mathrm{e}}_3^{\mathrm{T}}{\mathrm{e}}_1^{\prime }\right)\\ & ={\mathrm{e}}_1^{\mathrm{T}}{\mathrm{e}}_1^{\prime }{\mathrm{e}}_1^{\mathrm{T}}{\mathrm{e}}_1^{\prime }+{\mathrm{e}}_2^{\mathrm{T}}{\mathrm{e}}_1^{\prime }{\mathrm{e}}_2^{\mathrm{T}}{\mathrm{e}}_1^{\prime }+{\mathrm{e}}_3^{\mathrm{T}}{\mathrm{e}}_1^{\prime }{\mathrm{e}}_3^{\mathrm{T}}{\mathrm{e}}_1^{\prime }\\ & =({\mathrm{e}}_1^{\mathrm{T}}{\mathrm{e}}_1^{\prime }{\mathrm{e}}_1^{\mathrm{T}}+{\mathrm{e}}_2^{\mathrm{T}}{\mathrm{e}}_1^{\prime }{\mathrm{e}}_2^{\mathrm{T}}+{\mathrm{e}}_3^{\mathrm{T}}{\mathrm{e}}_1^{\prime }{\mathrm{e}}_3^{\mathrm{T}}){\mathrm{e}}_1^{\prime }\\ & =({\mathrm{e}}_1^{\prime \mathrm{T}}{\mathrm{e}}_1{\mathrm{e}}_1^{\mathrm{T}}+{\mathrm{e}}_1^{\prime \mathrm{T}}{\mathrm{e}}_2{\mathrm{e}}_2^{\mathrm{T}}+{\mathrm{e}}_1^{\prime \mathrm{T}}{\mathrm{e}}_3{\mathrm{e}}_3^{\mathrm{T}}){\mathrm{e}}_1^{\prime }\\ & =({\mathrm{e}}_1^{\prime }{)}^{\mathrm{T}}({\mathrm{e}}_1{\mathrm{e}}_1^{\mathrm{T}}+{\mathrm{e}}_2{\mathrm{e}}_2^{\mathrm{T}}+{\mathrm{e}}_3{\mathrm{e}}_3^{\mathrm{T}}){\mathrm{e}}_1^{\prime }\\ & =({\mathrm{e}}_1^{\prime }{)}^{\mathrm{T}}{\mathrm{e}}_1^{\prime }\\ & =1\end{array}$$
由于
$$1=\det (\mathrm{I})=\det ({\mathrm{R}}^{\mathrm{T}}\mathrm{R})=\det ({\mathrm{R}}^{\mathrm{T}})\det (\mathrm{R})=(\det (\mathrm{R}){)}^2$$
所以
$$\det (R)=\pm 1$$
按照定义可得

（2）$\epsilon$ 的维度是3，$\eta$ 的维度是1。

（3）设 $q_1=[{\epsilon }_1,{\eta }_1{]}^T,q_2=[{\epsilon }_2,{\eta }_2{]}^T$

$$\begin{array}{rl}\therefore q_1{q}_2& =[{\eta }_1{\epsilon }_2+{\eta }_2{\epsilon }_1+{\epsilon }_1\times {\epsilon }_2,{\eta }_1{\eta }_2-{\epsilon }_1^T{\epsilon }_2{]}^T\\ & \\ \therefore q_1^{+}{q}_2& =\left[\begin{array}{cc}{\eta }_{1}1-{\epsilon }_1^{\times }& {\epsilon }_1\\ -{\epsilon }_1^{\mathrm{T}}& {\eta }_1\end{array}\right]\left[\begin{array}{c}{\epsilon }_2\\ {\eta }_2\end{array}\right]\\ & =[{\eta }_1{\epsilon }_2+{\epsilon }_1^{\times }{\epsilon }_2+{\epsilon }_1{\eta }_2,{\eta }_1{\eta }_2-{\epsilon }_1^T{\epsilon }_2{]}^T\\ & =q_1{q}_2\\ & \\ q_2^{\oplus }{q}_1& =\left[\begin{array}{cc}{\eta }_{2}1+{\epsilon }_2^{\times }& {\epsilon }_2\\ -{\epsilon }_2^{\mathrm{T}}& {\eta }_2\end{array}\right]\left[\begin{array}{c}{\epsilon }_1\\ {\eta }_1\end{array}\right]\\ & =[{\eta }_2{\epsilon }_1-{\epsilon }_1^{\times }{\epsilon }_2+{\epsilon }_2{\eta }_1,-{\epsilon }_2^T{\epsilon }_1+{\eta }_2{\eta }_1{]}^T\\ & =[{\eta }_2{\epsilon }_1+{\epsilon }_2^{\times }{\epsilon }_1+{\epsilon }_2{\eta }_1,-{\epsilon }_1^T{\epsilon }_2+{\eta }_2{\eta }_1{]}^T\\ & =q_1{q}_2\end{array}$$

罗德里格斯公式的证明 (2 分，约 1 小时)

罗德里格斯公式描述了从旋转向量到旋转矩阵的转换关系。设旋转向量长度为 θ，方向为 $n$，那么旋转矩阵 $R$ 为：
$$R=\cos \theta I-(1-\cos \theta ){\mathbf{nn}}^T+\sin \theta {\mathbf{n}}^{\wedge }.\text{\hspace{1em}(4)}$$
我们在课程中仅指出了该式成立，但没有给出证明。请你证明此式。

提示：参考https://en.wikipedia.org/wiki/Rodrigues%27_rotation_formula。

四元数运算性质的验证 (1 分，约 1 小时)

课程中介绍了单位四元数可以表达旋转。其中，在谈论用四元数 $q$ 旋转点 $p$ 时，结果为：
$$p=qp{q}^{-1}.\text{\hspace{1em}(5)}$$
我们说，此时 $p\prime$ 必定为虚四元数（实部为零）。请你验证上述说法。

此外，上式亦可写成矩阵运算：$p^{\prime }=Qp$。请根据你的推导，给出矩阵 $Q$。注意此时 $p$ 和 $p\prime$ 都是四元数形式的变量，所以 $Q$ 为 4 × 4 的矩阵。

提示：如果使用第 4 题结果，那么有：
$$\begin{array}{rl}{p}^{\prime }& =qp{q}^{-1}=q^{+}{p}^{+}{q}^{-1}\\ & =q^{+}{q}^{-1^{\oplus }}v.\end{array}\text{\hspace{1em}(6)}$$
从而可以导出四元数至旋转矩阵的转换方式：
$$R=q^{+}{q}^{-1^{\oplus }}.\text{\hspace{1em}(7)}$$

*熟悉 C++11 (2 分，约 1 小时)

请注意本题为附加题。

C++ 是⼀门古老的语言，但它的标准至今仍在不断发展。在 2011 年、2014 年和 2017 年，C++ 的标准又进行了更新，被称为 C++11，C++14，C++17。其中，C++11 标准是最重要的⼀次更新，让 C++发生了重要的改变，也使得近年来的 C++ 程序与你在课本上（比如谭浩强）学到的 C++ 程序有很⼤的不同。你甚至会惊叹这是⼀种全新的语言。C++14 和 C++17 则是对 11 标准的完善与扩充。

越来越多的程序开始使用 11 标准，它也会让你在写程序时更加得心应手。本题中，你将学习⼀些 11标准下的新语法。请参考本次作业 books/目录下的两个 pdf，并回答下面的问题。

设有类 A，并有 A 类的⼀组对象，组成了⼀个 vector。现在希望对这个 vector 进行排序，但排序的方式由A.index 成员大小定义。那么，在 C++11 的语法下，程序写成：

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

class A {
public:
	A(const int& i ) : index(i) {}
  int index = 0;
};

int main() {
	A a1(3), a2(5), a3(9);
	vector<A> avec{a1, a2, a3};
	std::sort(avec.begin(), avec.end(), [](const A&a1, const A&a2) {return a1.index<a2.index;});
	for ( auto& a: avec ) cout<<a.index<<" ";
	cout<<endl;
return 0;
}

请说明该程序中哪些地方用到了 C++11 标准的内容。提示：请关注范围 for 循环、自动类型推导、lambda表达式等内容。

补充习题

有两个右手系1和2，其中2系的x轴与1系的y轴方向相同，2系的y轴与1系z轴方向相反，2系的z轴与1系的x轴相反，两个坐标系原点重合，求R12，求1系中(1,1,1)在2系中的坐标。请自己编写一个c++程序实现它，并用Cmake编译，得到能输出答案的可执行文件

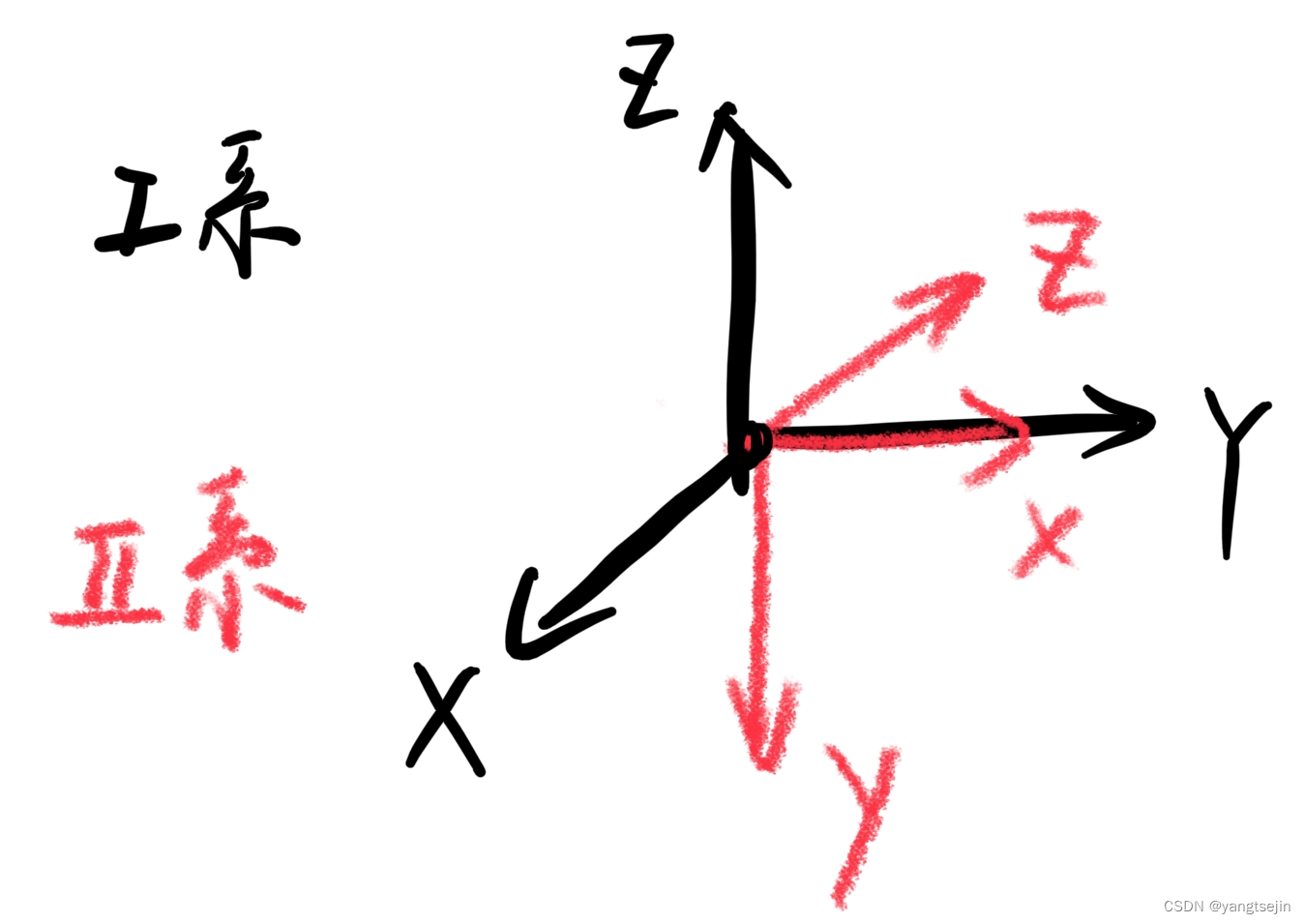
这个过程会迫使我们思考到底是坐标系变换，如何从零写出一个变换，如何使用坐标变化来改变点的坐标；你会对欧拉角的使用，尤其是动静轴和旋转顺序印象极其深刻

---

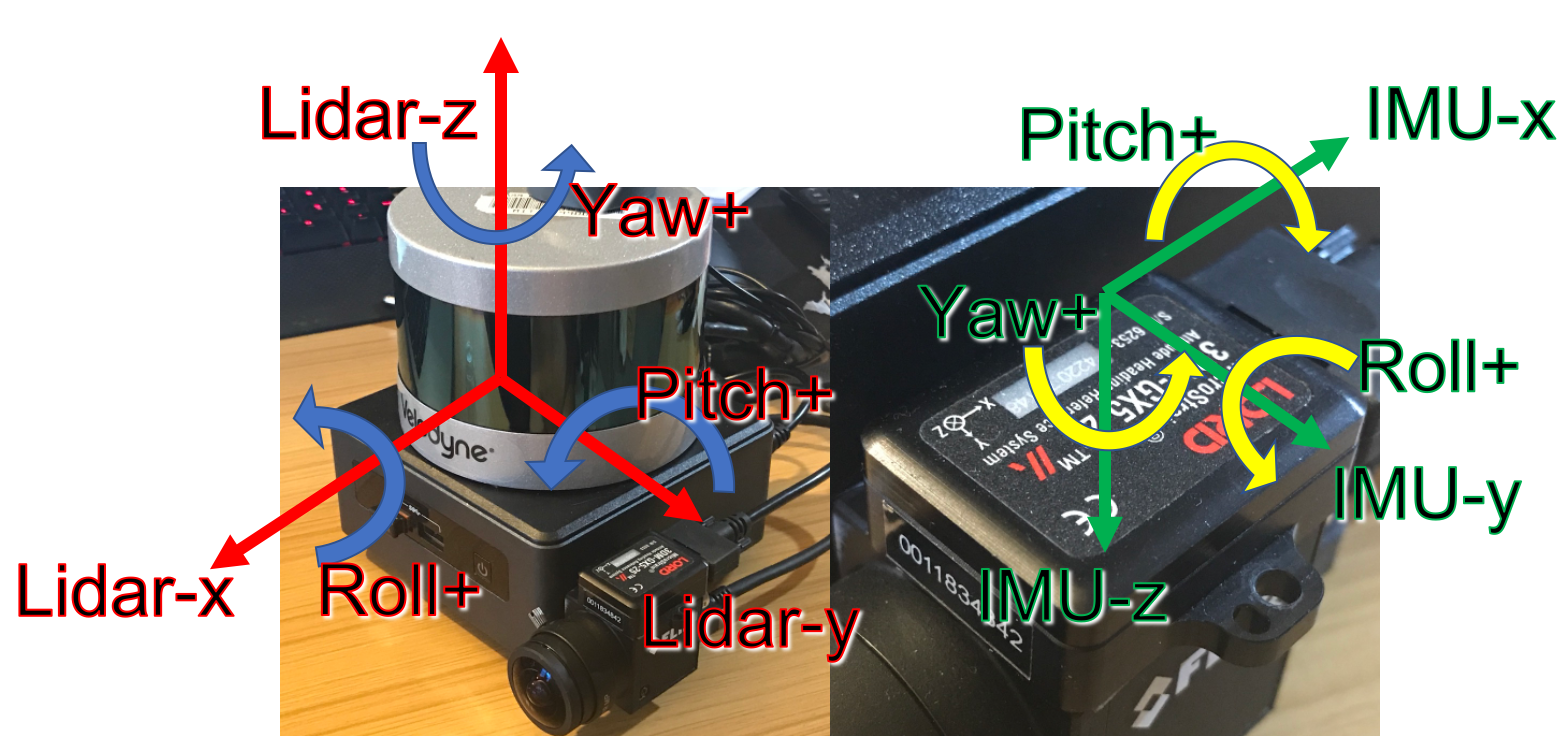
1. 若⾏列式为-1，通常称为瑕旋转（inproper rotation，对应物理当中旋转 + 镜像）。 ↩︎