L0 Smoothing 笔记（一）

          本文是Image Smoothing via L0 Gradient Minimization的学习笔记，大部分来自笔者对原文的翻译。笔者计算数学系小白一枚，初次接触图像处理，这是阅读的第一篇相关论文，如果笔记有所偏差，还望读者批评指正。

     所谓图像平滑，就是将图像中无关紧要的细节去除，而只保留显著的边缘部分。L0范数可以理解为向量中非零元素的个数。而L0 Smoothing是通过控制非零图像梯度的数目来增强图像显著边缘部分，以此达到图像的全局优化。

（一）原理

 1）一维平滑

    用g来表示原始输入的离散信号，用f来表示信号平滑处理后的结果。此方法直接计数幅度的变化，其数学表达式为：

                                                               （1）

     其中，p和p+1和分别表示相邻采样信号或者像素值，|fp-fp+1|示相邻信号间的梯度，信号之间采用向前差分的形式求解梯度。#{}表示一个统计操作，用来统计满足|fp-fp+1|不等于零的信号p的数目，即图像梯度的L₀范数。c(f)不依赖于梯度本身，因此如果只改变其边缘对比度，它的值不会受到影响。这个离散计数函数是此法的核心。

    但是仅仅有这一项是毫无意义的。在我该方法中，它与一般的约束项结合，即，结果f应该在结构上类似于输入信号g。具体的目标函数是：

                                                      （2）

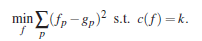
    c(f)＝k表示结果中存在k个非零梯度。k越大，近似越精细。实际上，k的取值可能从几十到几千不等，尤其是在具有不同分辨率的二维图像中。为了控制k的取值，采用一般方程的形式在平滑项和保真项之间寻求一种平衡，并将其写为：

                                                         （3）

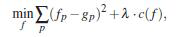
    其中，lambda是控制着平滑项的权重参数，其数值越大，信号平滑的就越严重。通过下图可以看出该法的优点：

                

2）二维规划

    在二维图像表示中，用I表示输入图像，用S表示计算结果。Sp的梯度是用来计算对于每一个像素点p，在x（水平）和y（垂直）方向上，它们与相邻像素间的颜色差异。此法的梯度测量（图像梯度的L₀范数的测量）可表示为：