为了验证因果效应,最直接有效的就是做AB实验。一组保持原状,另一组做出对应改变,如果两组的差异超出了正常数据波动范围,我们就认为两组的差异是这个改变所引起的,差异就是因果效应。但是呢,很多时候我们出于各种原因,无法做严格的AB实验,只能基于观察数据验证因果效应。此时就是因果推断的用武之地了。PSM(倾向性得分匹配)正是因果推断中的一种。
PSM的朴素思想
用大白话来说,就是我们从观察数据中筛选出两波在各个属性尽可能都相似的人,让他们仅在待验证变量上不一致,这样就是一个【伪AB实验】了,两波人的差异就可以粗略认为是待验证变量带来的因果效应。

如果属性很少,那可以直接一对一的找每个相似的属性就行;但是往往属性很多,对每个属性都直接找类似的效率很低,也不好找到一模一样的,毕竟世界上没有两片一模一样的树叶,这就需要“九九归一”,把多个属性转换成一个值,这样就方便找相似的ta了。
比如现在我们要验证上大学对于工资的因果效应的话,我们应该找出来两波在家庭、外貌、智商、情商等等各个方面尽可能都相似的人,差异就在一波人上了大学,一波人没有上大学,他们工资的差异就可以被认为是上大学带来的效应。这个案例中如果直接在每个属性都找相似的,找起来很慢又很难。那我们有没有办法可以把多个属性量化成一个值呢?比如把家庭、外貌、智商、情商等量化成【上大学的概率】,这样我们就可以直接拿这个【上大学的概率】匹配出两波人了。
恭喜你,上面的思路其实正是PSM(倾向性得分匹配)的核心,PSM就是利用logit等模型把多个属性转换成一个值:倾向性得分。倾向性得分代表某个用户或者样本在是否进入实验组(即待验证变量为1的一组)的概率,在上面的案例中则就是上大学的概率。
用函数表示的话,输入:某个用户或者样本的各种属性,输出:是否在实验组,用这个拟合模型后即可针对每个用户或者样本计算倾向性得分。
恭喜你,上面的思路其实正是PSM(倾向性得分匹配)的核心,PSM就是利用logit等模型把多个属性转换成一个值:倾向性得分。用函数表示的话,输入:某个用户或者样本的各种属性,输出:是否在实验组,用这个拟合模型后即可针对每个用户或者样本计算倾向性得分。倾向性得分代表某个用户或者样本在是否进入实验组(即待验证变量为1的一组)的概率,在上面的案例中则就是上大学的概率。
基于这个倾向性得分我们就可以匹配出来属性相似的实验组和对照组,就可以沿着AB实验那一套做假设检验了。所以PSM其实就三步走:
- 第一步建模型计算倾向性得分
- 第二步用倾向性得分匹配实验样本
- 第三步就是假设检验出结论。
Python实现PSM
本次用的数据集是一个人力资源管理领域的数据,主要包含各员工工作相关的数据和指标,可以在和鲸平台下载。

本次我们分析的目的是研究【性别对于月收入的因果效应】,从图上可以似乎可以直观看到男性比女性工资高,但是很难保证用于比较的男女在其他属性上保持一致,所以害得用我们的PSM匹配一波再看。

1.处理数据
- 筛选属性数据,用于倾向性得分模型拟合,方便我们找到两波除了性别不一样其余属性都类似的用户
- 对类别类别变量转换成dummy变量
# 类别变量转换为dummy变量
dataset = pd.get_dummies(data = dataset,
drop_first=True)
dataset=dataset.reset_index(drop=False)
dataset.head()
2.建模获取倾向性得分
调用python的包psmpy拟合倾向性得分模型,需要把我们本次因果推断的结果【月收入】排除在外
## import libraries
from psmpy import PsmPy
## step1:建模
psm = PsmPy(dataset, treatment='Gender', indx='EmpID', exclude = ['MonthlyIncome'])
psm.logistic_ps(balance = True)
3.用倾向性得分匹配实验样本
psmpy自带的有knn模型用于匹配,如psm.knn_matched和psm.knn_matched_12n方法。但是经过我实践,在样本数一多的情况下经常跑不出来,或者花费时间很久,建议像下文中这样对倾向性得分分段后,再进行最近邻匹配。
##step2:匹配
predicted_data=psm.predicted_data
predicted_data_t=predicted_data[predicted_data['Gender']==1][['propensity_score','EmpID']]
predicted_data_c=predicted_data[predicted_data['Gender']==0][['propensity_score','EmpID']]
##按照propensity_score分组,方便快速匹配
list_value=[ i/10 for i in range(0,11)]
list_label=[ i for i in range(1,11)]
predicted_data_t['label']=pd.cut(predicted_data_t['propensity_score'],list_value,labels=list_label)
predicted_data_c['label']=pd.cut(predicted_data_c['propensity_score'],list_value,labels=list_label)
## KNN最近邻匹配
from tqdm import tqdm
import warnings
warnings.filterwarnings("ignore")
##取最近邻匹配,k=1
def get_min_dis_user(ps_t,data_input,label_n):
#在本区间,下一个区间内寻找最近的距离
data_c=data_input[data_input['label']==label_n]
if data_c.shape[0]<1:
data_c=data_input[data_input['label'].isin((label_n-1,label_n,label_n+1))]
else:
pass
data_c['ps_dis']=data_c['propensity_score'].map(lambda x: abs(x-ps_t))
data_c=data_c.sort_values(by=['ps_dis'])
min_dis_userid=data_c['user_id'].tolist()[0]
return min_dis_userid
match_id_list=[]
for i,row_t in tqdm(predicted_data_t.iterrows()):
match_id_list.append(get_min_dis_user(row_t['propensity_score'],predicted_data_c,row_t['label']))
4.匹配效果检验
- 倾向性得分分布
可以看到匹配前这两波人的倾向性得分分布明显不一样,而在匹配后两波人的倾向性得分分布趋于一致了,也就是之前可以很容易通过年龄、学历、工龄、职位等信息区分是男是女,经过匹配后这两波人在年龄、学历、工龄、职位等这些常用属性分布基本一致,基于这些信息已经很难判断是男是女了。


- 各属性分布检验
还要对一些重要的属性做检验,查看在两组内的分布有无显著差异。对于连续型指标,可以用Z检验或者T检验;对于离散型分类指标,可以用卡方检验。
5.AB实验及解读
经过我们前面的一系列匹配,我们可以认为我们构造了两波人,除了在性别上不一样,在年龄、学历、工龄、职位等均很相似。
通过AB实验常用的假设检验,我们发现两组人的月收入存在显著差异(P<0.05),男性比女性高了1813元,折算成比例则为39.4%。
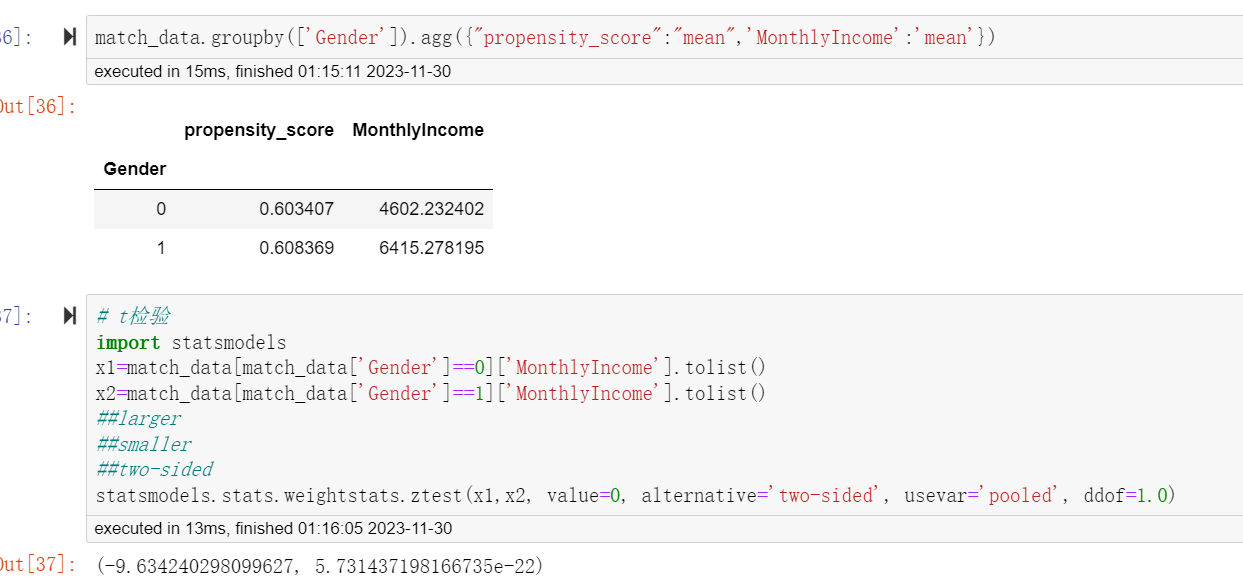
直观感受下匹配后男性和女性的月收入差异,可以看到基于这份数据看的话,均值的差异主要来自两端分布(低收入区间和高收入区间),在3000-6000区段内差异不大。
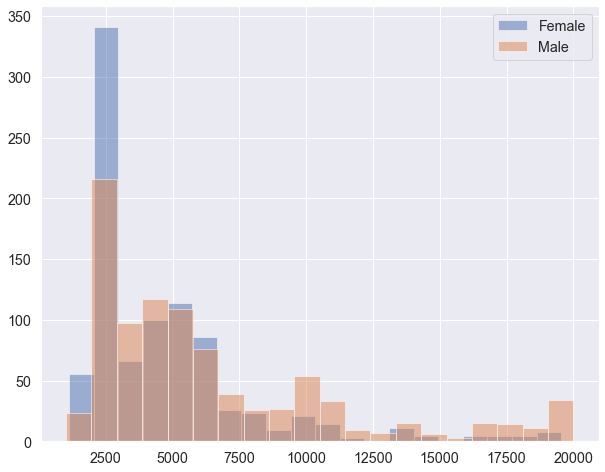
以上数据和结果仅供测试PSM用,不具有任何实际含义。对数据和相关代码感兴趣的小伙伴,公众号后台回复psm即可获取








 本文介绍了如何使用PSM(倾向性得分匹配)来验证性别对月收入的因果效应,通过数据预处理、建模计算倾向性得分、匹配相似样本并进行假设检验,展示了在Python中实施这一技术的过程。
本文介绍了如何使用PSM(倾向性得分匹配)来验证性别对月收入的因果效应,通过数据预处理、建模计算倾向性得分、匹配相似样本并进行假设检验,展示了在Python中实施这一技术的过程。

















 243
243

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










