离散数学(1)---集合论

第一章 集合论初步

1.1 集合的基本概念

• 我们把一些不同的确定的对象的全体称为集合。
• 集合中元素的性质：确定性、互异性、无序性。

1.2 集合代数

• 集合代数就是指集合之间的 交,并,补,差 运算.
• 摩根定律:

  ~(A∪B) = ~A ∩ ~B
  ~(A∩B) = ~A ∪~B

1.3 幂集

• 幂集: 由集合A的所有子集(包括空集以及A本身)所组成的集合叫做A的幂集, 记作p(A).
• 说明: 幂集是一个由集合构成的集合.

第二章 关系

2.1 关系的预备知识

• 有序偶: 两个按照一定次序排列的元素a,b 组成的一个有序序列, 称之为有序偶, 并记以<a, b>, 其中a, b 分别称为<a, b>的第一个分量和第二个分量.
• n元有序组: 将上述的有序偶推广为具有n个元素的有序序列, 即为n元有序组.
• 笛卡尔乘积: C = AxB = {<a ,b > | a ∈A, b∈B }, 即笛卡儿积是一个有序偶的集合.

2.2 关系的基本概念

• 关系: 从集合A到集合B的关系R是一些有序偶的集合, 这些有序偶是的第一分量是A中的一些元素, 第二分量是B的一些元素. 这个称为二元关系, 关系也可以拓展成为更多元的.
• 关系R中有序偶的第一分量所允许选区的对象的集合叫做关系R的定义域,记作D(R ), 第二分量叫做值域, 记作C(R ). 当D(R ) = C(R ) = M的时候, 称R 为集合M上的关系.
• 关系的自我理解: 关系就是一个集合, 这个集合中的元素就是二元有序偶, 一个有序偶<a,b>表示两个集合中的元素a,b 存在一定的关系.
• 关系的图表示: 是一个有向图, 若 有有序偶<a, b>, 则应该有从 结点a 指向 结点b 的一条有向边.

2.3 关系的运算

• 交并补差运算: 因为关系本身就是一集合, 所以可以进行交并补运算.
• 复合关系:
  
• 逆运算:
  

2.4 关系的重要性质

自反性 与 反自反性

• 在集合X上的关系R, 如果对任意 x∈X, 有(x,x)∈R,则称R是自反的.
• 在集合X上的关系R, 如果对任意 x∈X, 有(x,x) ∉ R,则称R是反自反的.
• 说明: 若X只有部分元素满足(x,x)∈R 或 (x,x)∉R ,则该关系既不是自反的也不是反自反的.

对称性 与 反对称性

• 在集合X上的关系R, 如果有(x,y) 属于R 必有 (y,x) ∈ R, 则称R是对称的.
• 在集合X上的关系R, 如果有(x,y) 属于R且x ≠ y, 必有 (y,x) ∉ R, 则称R是反对称的
• 说明: 同样,一个关系可以既不是对称的, 也不是反对称的

传递性

• 在集合X上的关系R, 如果有(x, y) ∈ R 且 (y, z) ∈ R , 则必有(x,z)属于R, 则成R是传递的.

2.5 关系上的闭包运算

闭包的概念

• 理解闭包: R的自反闭包, 就假设R有自反性, 然后根据这个自反性, 看是否能产生新的有序偶, 将新产生的有序偶加入到关系R中得到R’ , 则R’ 就是R的自反闭包. 对称闭包和传递闭包也一样.

闭包的构建

核心: 根据XXX闭包, 向关系R中添加满足XXX性质的有序偶:

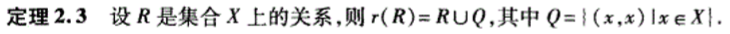
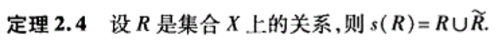
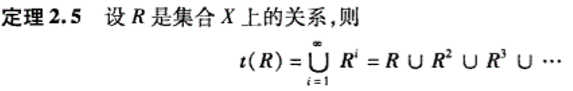
2.6 次序关系

• 概述: 次序, 顾名思义, 就是元素们是有序的, 就是元素可以按照一定顺序进行排序. 用离散中的概念来表达就是: 次序关系是一个满足反对称性以及传递性的关系. 次序关系又可以分为 偏序关系 和 拟序关系.

• 偏序和拟序：

  偏序关系: 集合X上的关系R如果是自反的, 反对称的, 传递的, 则称R在X上是偏序的.
  拟序关系： 集合X上的关系R如果是反自反的、传递的， 则称R在X上是拟序的。
  理解：
  偏序/拟序的核心就是 ：反自反，只有反自反了，才能说明两个元素谁先谁后，才有了“序”。

• 拟序的一个定理：集合X上的关系R如果是拟序号的，则必是反对称的。

• 偏序和拟序的关系：偏序具有对称性，拟序具有反对称性。

• 线性次序关系：

  
  理解： 就是集合X中，任意两个元素之前都可以用偏序关系R来关联，总能比出个前后。所以，X中的所有元素就可按照此偏序关系排列成为一列。
  eg： 字典次序关系 就是一种线性次序关系。

• 哈斯图：

  
  eg: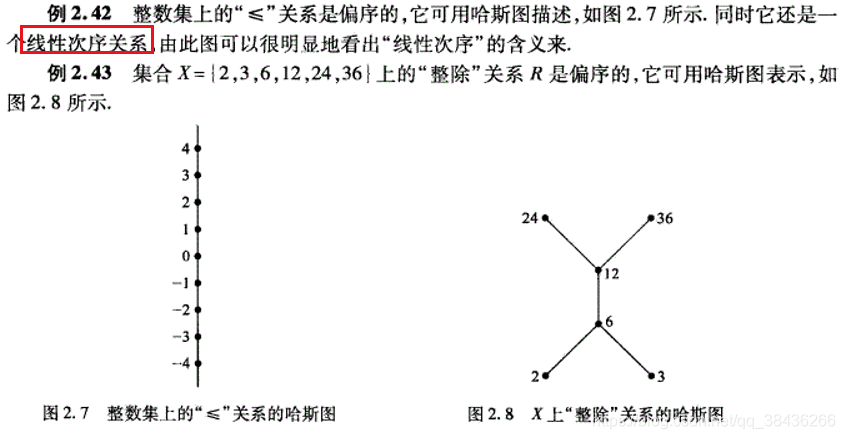
  可以看出，线性次序关系在哈斯图上的表现就是所有元素可以排成一条线。

2.7 相容关系

2.8 等价关系

等价关系： 一个在X上的关系R，如果它是自反的，对称的，传递的，则称此关系为等价关系。

同余关系：
理解：同余关系，顾名思义，就是具有相同余数。

等价类：
理解： 一个关系R可以把集合中的所有元素划分为多个 子集合。然后每个子集合中的任意两个元素，之间都有关系R。比如同余关系 就把集合中的元素划分成为多个等价类。

商集：
理解： 商集就是等价类的集合，就是说商集中的每个元素都是一个等价类。

第三章 函数

• 函数是一种特殊的关系
• 四种映射关系：
  • 满射： 值域中，每个像在定义域中都有一个原像。
  • 内射：值域中，有些像没有原像。
  • 单射：不同的原像，像也不同。即：不会两个原像映射到同一个像。
  • 多射：一个像可以由多个原像映射而来。
• 在关系中，任一关系均存在逆关系，但对于函数而言就不同了，一个函数不一定有反函数。因为函数是一个特殊的关系，因此必须要求函数是一一对应的，才会有反函数。

第四章 有限集和无限集

• 为了研究无限集，引入等势 的概念。
• 等势：集合A于集合B的元素之间，如果存在一一对应的关系，则称A与B等势，记 A~B

  eg: N={0,1,2,3,…} S={1,3,5,7,…}
  则有：
  0 1 2 3,…
  1 2 5 7,…
  如上所示，能找到某种规律让两个集合中的元素能够一一对应，则说明两个集合等势。

• 定理：若一个集合为无限集，则它必含有与其等势的真子集。
• 可列集：与自然数集N等势的集合叫做可列集。
• 无限集的“大小”问题：
  • 自然数集是无限集中“最小”的集合。 其基数为ℵ₀（阿列夫零）
  • 因为所有的可列集和自然数集N等势，因此所有可列集的基数均为ℵ₀。
  • 实数集R是不可列的，实数集的大小比可列集大。