大学“电路分析基础”考试必备试题合集第十章（终）,呕心沥血，为了让千万为考试抓耳挠腮的people不挂科，特意整理了10篇考试题库，请施主收下。

沄边小卖部

已于 2022-05-30 11:11:43 修改

阅读量2.8k

点赞数 3

分类专栏：大学考试 # “电路分析基础”试题合集电路分析基础文章标签：笔记资料

于 2022-05-11 22:45:47 首次发布

本文链接：https://blog.csdn.net/qq_38639612/article/details/124719086

版权

大学同时被 3 个专栏收录

17 篇文章

订阅专栏

考试

12 篇文章

订阅专栏

电路分析基础

10 篇文章

订阅专栏

“电路分析基础”试题合集第十章

一、填空题（每空1分）

二、判断下列说法的正确与错误（每小题1分）

三、单项选择题（每小题2分）

四、简答题（每小题3～5分）

五、计算分析题（每题6～12分）

一、填空题（每空1分）

1、一系列最大值不同，频率成整数倍的正弦波，叠加后可构成一个非正弦周期波。

2、与非正弦周期波频率相同的正弦波称为非正弦周期波的基波；是构成非正弦周期波的基本成分；频率为非正弦周期波频率奇次倍的叠加正弦波称为它的奇次谐波；频率为非正弦周期波频率偶次倍的叠加正弦波称为它的偶次谐波。

3、一个非正弦周期波可分解为无限多项谐波成分，这个分解的过程称为谐波分析，其数学基础是傅里叶级数。

4、所谓谐波分析，就是对一个已知波形的非正弦周期信号，找出它所包含的各次谐波分量的振幅和频率，写出其傅里叶级数表达式的过程。

5、方波的谐波成分中只含有正弦成分的各奇次谐波。

6、如果非正弦波的后半周与波形的前半周具有镜象对称关系，就具有奇次对称性，具有奇次对称性的周期信号只具有奇次谐波成分，不存在直流成分和偶次谐波成分，其波形对原点对称。

7、若非正弦周期信号波形的后半周完全重复前半周的变化，就具有偶次对称性，这种非正弦波除了含有直流成分以外，还包含一系列的偶次谐波，这种特点的非正弦波的波形对纵轴对称。

8、频谱是描述非正弦周期波特性的一种方式，一定形状的波形与一定结构的频谱相对应。非正弦周期波的频谱是离散频谱。

9、非正弦周期量的有效值与正弦量的有效值定义相同，但计算式有很大差别，非正弦量的有效值等于它的各次谐波有效值的平方和的开方。

10、只有同频率的谐波电压和电流才能构成平均功率，不同频率的电压和电流是不能产生平均功率的。数值上，非正弦波的平均功率等于它的各次谐波单独作用时所产生的平均功率之和。

二、判断下列说法的正确与错误（每小题1分）

1、非正弦周期波各次谐波的存在与否与波形的对称性无关。（ × ）

2、正确找出非正弦周期量各次谐波的过程称为谐波分析法。（ ∨ ）

3、具有偶次对称性的非正弦周期波，其波形具有对坐标原点对称的特点。（ × ）

4、方波和等腰三角波相比，含有的高次谐波更加丰富。（ ∨ ）

5、方波和等腰三角波相比，波形的平滑性要比等腰三角波好得多。（ × ）

6、非正弦周期量的有效值等于它各次谐波有效值之和。（ × ）

7、非正弦周期量作用的电路中，电感元件上的电流波形平滑性比电压差。（ × ）

8、非正弦周期量作用的线性电路中具有叠加性。（ ∨ ）

9、非正弦周期量作用的电路中，电容元件上的电压波形平滑性比电流好。（ ∨ ）

10、波形因数是非正弦周期量的最大值与有效值之比。（ × ）

三、单项选择题（每小题2分）

1、任意给出几种常见的非正弦周期信号波形图，你能否确定其傅里叶级数展开式中有无恒定分量（ B ）

A、不能 B、能 C、不确定

2、某方波信号的周期T=5μs，则此方波的三次谐波频率为（ C ）

A、106Hz B、2×106Hz C、6×105Hz

3、周期性非正弦波的傅里叶级数展开式中，谐波的频率越高，其幅值越（ B ）

A、大 B、小 C、无法判断

4、一个含有直流分量的非正弦波作用于线性电路，其电路响应电流中（ A ）

A、含有直流分量 B、不含有直流分量 C、无法确定是否含有直流分量

5、非正弦周期量的有效值等于它各次谐波（ B ）平方和的开方。

A、平均值 B、有效值 C、最大值

6、非正弦周期信号作用下的线性电路分析，电路响应等于它的各次谐波单独作用时产生的响应的（ B ）的叠加。

A、有效值 B、瞬时值 C、相量

7、已知一非正弦电流 $\large i(t)=(10+10\sqrt{2}\sin2\omega t)$ A，它的有效值为（ B ）

A、 $\large 20\sqrt{2}$ A B、 $\large 10\sqrt{2}$ A C、20A

8、已知基波的频率为120Hz，则该非正弦波的三次谐波频率为（ A ）

A、360Hz B、300Hz C、240Hz

四、简答题（每小题3～5分）

1、什么叫周期性的非正弦波，你能举出几个实际中的非正弦周期波的例子吗？

答：周而复始地重复前面循环的非正弦量均可称为周期性非正弦波，如等腰三角波、矩形方波及半波整流等。

2、周期性的非正弦线性电路分析计算步骤如何，其分析思想遵循电路的什么原理？

答：周期性的非正弦线性电路的分析步骤为：

①根据已知傅里叶级数展开式分项，求解各次谐波单独作用时电路的响应；

②求解直流谐波分量的响应时，遇电容元件按开路处理，遇电感元件按短路处理；

③求正弦分量的响应时按相量法进行求解，注意对不同频率的谐波分量，电容元件和电感元件上所呈现的容抗和感抗各不相同，应分别加以计算；

④用相量分析法计算出来的各次谐波分量的结果一般是用复数表示的，不能直接进行叠加，必须要把它们化为瞬时值表达式后才能进行叠加。

周期性非正弦线性电路分析思想遵循线性电路的叠加定理。

3、非正弦周期信号的谐波分量表达式如何表示？式中每一项的意义是什么？

答：非正弦周期信号的谐波分量表达式是用傅里叶级数展开式表示的，式中的每一项代表非正弦量的一次谐波。

4、何谓基波？何谓高次谐波？什么是奇次谐波和偶次谐波？

答：频率与非正弦波相同的谐波称为基波，它是非正弦量的基本成分；二次以上的谐波均称为高次谐波；谐波频率是非正弦波频率的奇数倍时称为奇次谐波；谐波频率是非正弦波频率的偶数倍时称为偶次谐波。

5、能否定性地说出具有奇次对称性的波形中都含有哪些谐波成分？

答：具有奇次对称性的非正弦周期波中，只具有奇次谐波成分，不存在直流成分及偶次谐波成分。

6、“只要电源是正弦的，电路中各部分电流及电压都是正弦的”说法对吗？为什么？

答：说法不对！电源虽然是正弦的，但是如果电路中存在非线性元件，在非线性元件上就会出现非正弦响应。

7、波形的平滑性对非正弦波谐波有什么影响？为什么？

答：非正弦波所包含的高次谐波的幅度是否显著，取决于波形的平滑性，因此波形的平滑性对非正弦波谐波影响很大。如稳恒直流电和正弦波，平滑性最好，不含有高次谐波；而方波和尖脉冲波，由于平滑性极差而含有丰富的高次谐波。

8、非正弦波的“峰值越大，有效值也越大”的说法对吗？试举例说明。

答：这种说法对正弦量是对的，对非正弦量就不对。例如一个方波的峰值和等腰三角波的峰值相比，如果等腰三角波的峰值大于方波，但等腰三角波的有效值不一定比方波大。

五、计算分析题（每题6～12分）

1、图5.1所示电路，已知R=20Ω，ωL=20Ω， $\large u(t)=(25+100\sqrt{2}\sin \omega t+25\sqrt{2}\sin \omega t+10\sqrt{2}\sin 3\omega t )$ V，求电流的有效值及电路消耗的平均功率。

解：直流分量单独作用时：I=25/20=1.25A;

基波单独作用时： $\large I_{1}=\frac{100}{\sqrt{20^{2}+20^{2}}}\approx 3.536A$

二次谐波单独作用时： $\large 2\omega L= 40$ Ω $\large I_{2}=\frac{25}{\sqrt{20^{2}+40^{2}}}\approx 0.559A$

三次谐波单独作用时： 3 $\large \omega$ L=60Ω $\large I_{3}=\frac{10}{\sqrt{20^{2}+60^{2}}}\approx 0.158A$

所以电流的有效值： $\large I= \sqrt{1.25^{2}+3.536^{2}+0.559^{2}+0.158^{2}} \approx 3.795A$

直流分量功率： $\large P_{0}$ =25*1.25=31.25W

一次谐波功率： $\large P_{1}=3.536^{2}*10 \approx 250W$

二次谐波功率： $\large P_{2}$ =0.559*0.559*20≈6.25W

三次谐波功率： $\large P_{3}$ =0.158*0.158*20≈0.5W

电路消耗的平均功率：P≈31.25+250+6.25+0.5=288W；

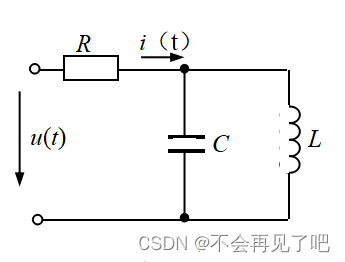
2、电路如图1.2所示，已知R=20Ω，基波ωL=10/3Ω， $\large u(t)=(200+100\sqrt{2}\sin 3\omega t)V$ V，基波1/ωC=60Ω，求电流的i(t)及电感两端电压 $\large u_{L}$ 的谐波表达式。

解：直流分量单独作用时：I =200/20=10A ;

三次谐波单独作用时：3ωL=10Ω,1/3ωC=20Ω,

$\large Z_{3}=20+\frac{j10(-j20)}{-j20}=20+j20$ =28.28∠45°Ω，

$\large I_{3}$ =100/28.28∠45°≈3.536∠-45°A；

$\large i(t)=10+5sin(3\omega t-45^{\circ})A$ ;

$\large u_{L}(t)=100\sin (3\omega t+45^{\circ})V$ .

3、已知图1.3所示电路的 $\large u(t)=\left [ 10+80\sin (\omega t+30^{\circ})+18\sin3\omega t \right ]V$ ，R=6Ω，ωL=2Ω，1/ωC=18Ω，求交流电压表、交流电流表及功率表的读数，并求i(t)的谐波表达式。

解：基波单独作用时：I0=0 U0=0 W0=0，

一次谐波单独作用时： $\large Z_{1}=6+j(2-18)\approx 17.1\angle -69.4^{\circ}\Omega$ ,

$\large I_{1}=\frac{80/\sqrt{2}\angle 30^{\circ}}{17.1\angle -69.4^{\circ}}\approx 3.31\angle 99.4^{\circ}A$ ;

RL串联部分电压有效值： $\large U_{RL}=3.31*6.32\approx 20.9V$ ;

三次谐波单独作用时： $\large Z_{1}=6+j(6-6)=6\angle 0^{\circ}\Omega$ 发生串联谐振,

RL串联部分电压有效值： $\large U_{RL3}=2.12*8.48\approx 18V$ ;

电流表读数： $\large I= \sqrt{3.31^{2}+2.12^{2}}\approx 3.93A$ ;

电压表读数： $\large U= \sqrt{20.9^{2}+18^{2}}\approx 27.6V$ ;

功率表读数： $\large P=P_{1}+P_{2}=3.31*56.56*\cos 69.4^{\circ}+2.12^{2}*6=92.9W$

4、图1.4所示电路，已知L=10mH，u为非正弦波，已知电阻中的电流当频率为基波频率f=50KHz时达到最大值，而当信号频率为100KHz时，电阻中的电流为零，求两个电容的数值。

解：据题意可知，基波单独作用时，电路发生串联谐振，当二次谐波单独作用时，并联组合发生并联谐振，由并联谐振可得 $\large C_{1}=\frac{1}{(2*6.28*50000)^{2}*0.01}\approx 254$ pf

基波时： $\large Z_{LC1}=\frac{j(3.14)(-j12.5)}{-j9.36}\approx j4.19K\Omega$ ;

与C2发生串谐，则 $\large C_{2}=\frac{1}{4.19*10^{3}*314000}\approx 760$ pF。