- 感知器和S型神经元简介
1.1感知器
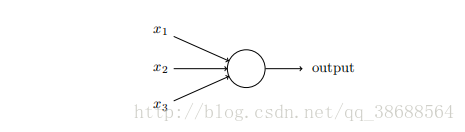
感知器是如何⼯作的呢?⼀个感知器接受⼏个⼆进制输⼊,x1, x2, …,并产⽣⼀个⼆进制输出:
⽰例中的感知器有三个输⼊,x1, x2, x3。通常可以有更多或更少输⼊。Rosenblatt 提议⼀个简单的规则来计算输出。他引⼊权重,w1, w2, …,表⽰相应输⼊对于输出重要性的实数。神经元的输出,0 或者 1,则由分配权重后的总和 ∑j wjxj ⼩于或者⼤于⼀些阈值决定。和权重⼀样,阈值是⼀个实数,⼀个神经元的参数。⽤更精确的代数形式:
这就是⼀个感知器所要做的所有事!
1.2 S型神经元
假设我们有⼀个感知器⽹络,想要⽤它来解决⼀些问题。例如,⽹络的输⼊可以是⼀幅⼿写数字的扫描图像。我们想要⽹络能学习权重和偏置,这样⽹络的输出能正确分类这些数字。为了看清学习是怎样⼯作的,假设我们把⽹络中的权重(或者偏置)做些微⼩的改动。就像我们⻢上会看到的,这⼀属性会让学习变得可能。这⾥简要⽰意我们想要的(很明显这个⽹络对于⼿写识别还是太简单了!):
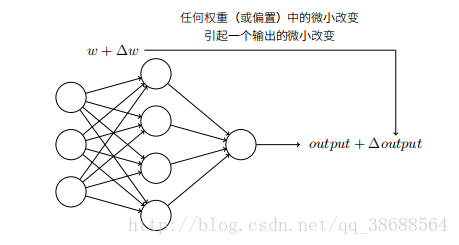
如果对权重(或者偏置)的微⼩的改动真的能够仅仅引起输出的微⼩变化,那我们可以利⽤这⼀事实来修改权重和偏置,让我们的⽹络能够表现得像我们想要的那样。例如,假设⽹络错误地把⼀个“9”的图像分类为“8”。我们能够计算出怎么对权重和偏置做些⼩的改动,这样⽹络能够接近于把图像分类为“9”。然后我们要重复这个⼯作,反复改动权重和偏置来产⽣更好的输出。这时⽹络就在学习。问题在于当我们的⽹络包含感知器时这不会发⽣。实际上,⽹络中单个感知器上⼀个权重或偏置的微⼩改动有时候会引起那个感知器的输出完全翻转,如 0 变到 1。那样的翻转可能接下来引起其余⽹络的⾏为以极其复杂的⽅式完全改变。因此,虽然你的“9”可能被正确分类,⽹络在其它图像上的⾏为很可能以⼀些很难控制的⽅式被完全改变。这使得逐步修改权重和偏置来
让⽹络接近期望⾏为变得困难。也许有其它聪明的⽅式来解决这个问题。但是这不是显⽽易⻅地能让⼀个感知器⽹络去学习。
我们可以引⼊⼀种称为 S 型神经元的新的⼈⼯神经元来克服这个问题。S 型神经元和感知器类似,但是被修改为权重和偏置的微⼩改动只引起输出的微⼩变化。这对于让神经元⽹络学习起来是很关键的。好了 让我来描述下 S 型神经元。我们⽤描绘感知器的相同⽅式来描绘 S 型神经元:
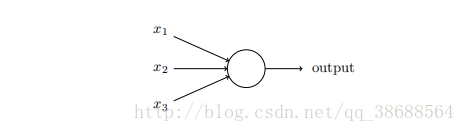
正如⼀个感知器,S 型神经元有多个输⼊,x1, x2, …。但是这些输⼊可以取 0 和 1 中的任意值,⽽不仅仅是 0 或 1。例如,0.638 … 是⼀个 S 型神经元的有效输⼊。同样,S 型神经元对每个输⼊有权重,w1, w2, …,和⼀个总的偏置,b。但是输出不是 0 或 1。相反,它现在是 σ(w · x+b),这⾥ σ 被称为 S 型函数1,定义为:
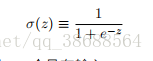
为了理解和感知器模型的相似性,假设 z ≡ w · x + b 是⼀个很⼤的正数。那么 e^(−z) ≈ 0 ⽽σ(z) ≈ 1。即,当 z = w · x + b 很⼤并且为正,S 型神经元的输出近似为 1,正好和感知器⼀样。相反地,假设 z = w · x + b 是⼀个很⼤的负数。那么 e^(−z) → ∞σ(z) ≈ 0。所以当 z = w · x + b是⼀个很⼤的负数,S 型神经元的⾏为也⾮常近似⼀个感知器。只有在 w · x + b 取中间值时,和
感知器模型有⽐较⼤的偏离。σ 的代数形式⼜是什么?我们怎样去理解它呢?实际上,σ 的精确形式不重要 —— 重要的是这个函数绘制的形状。是这样:
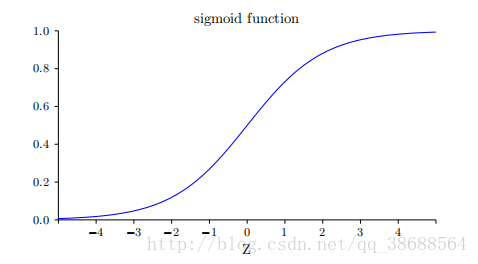
这个形状是阶跃函数平滑后的版本:
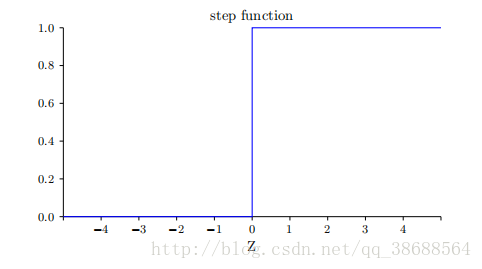
如果 σ 实际是个阶跃函数,既然输出会依赖于 w · x + b 是正数还是负数2,那么 S 型神经元会成为⼀个感知器。利⽤实际的 σ 函数,我们得到⼀个,就像上⾯说明的,平滑的感知器。的确,σ 函数的平滑特性,正是关键因素,⽽不是其细部形式。σ 的平滑意味着权重和偏置的微⼩变化,即 ∆wj 和 ∆b,会从神经元产⽣⼀个微⼩的输出变化 ∆output。实际上,微积分告诉我们∆output 可以很好地近似表⽰为:
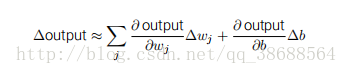
我们应该如何解释⼀个 S 型神经元的输出呢?很明显,感知器和 S 型神经元之间⼀个很⼤的不同是 S 型神经元不仅仅输出 0 或 1。它可以输出 0 和 1 之间的任何实数,所以诸如 0.173 … 和
0.689 … 的值是合理的输出。这是⾮常有⽤的,例如,当我们想要输出来表⽰⼀个神经⽹络的图像像素输⼊的平均强度。但有时候这会是个⿇烦。假设我们希望⽹络的输出表⽰“输⼊图像是
⼀个 9”或“输⼊图像不是⼀个 9”。很明显,如果输出是 0 或 1 是最简单的,就像⽤感知器。但是在实践中,我们可以设定⼀个约定来解决这个问题,例如,约定任何⾄少为 0.5 的输出为表⽰“这是⼀个 9”,⽽其它⼩于 0.5 的输出为表⽰“不是⼀个 9”。当我们正在使⽤这样的约定时,我总会清楚地提出来,这样就不会引起混淆。
1.3 神经网络的架构
前⾯提过,这个⽹络中最左边的称为输⼊层,其中的神经元称为输⼊神经元。最右边的,即输出层包含有输出神经元,在本例中,输出层只有⼀个神经元。中间层,既然这层中的神经元既不是输⼊也不是输出,则被称为隐藏层。“隐藏”这⼀术语也许听上去有些神秘 —— 我第⼀次听到这个词,以为它必然有⼀些深层的哲学或数学涵意 —— 但它实际上仅仅意味着“既⾮输⼊也⾮输出”。上⾯的⽹络仅有⼀个隐藏层,但有些⽹络有多个隐藏层。例如,下⾯的四层⽹络有两个隐藏层:
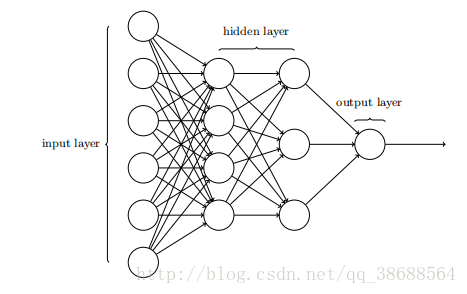
设计⽹络的输⼊输出层通常是⽐较直接的。例如,假设我们尝试确定⼀张⼿写数字的图像上是否写的是“9”。很⾃然地,我们可以将图⽚像素的强度进⾏编码作为输⼊神经元来设计⽹络。如果图像是⼀个 64 × 64 的灰度图像,那么我们会需要 4096 = 64 × 64 个输⼊神经元,每个强度取 0 和 1 之间合适的值。输出层只需要包含⼀个神经元,当输出值⼩于 0.5 时表⽰“输⼊图像不是⼀个 9”,⼤于 0.5 的值表⽰“输⼊图像是⼀个 9”。
相⽐于神经⽹络中输⼊输出层的直观设计,隐藏层的设计则堪称⼀⻔艺术。特别是通过⼀些简单的经验法则来总结隐藏层的设计流程是不可⾏的。相反,神经⽹络的研究⼈员已经为隐藏层开发了许多设计最优法则,这有助于⽹络的⾏为能符合⼈们期望的那样。例如,这些法则可以⽤于帮助权衡隐藏层数量和训练⽹络所需的时间开销。在本书后⾯我们会碰到⼏个这样的设计最优法则。
⽬前为⽌,我们讨论的神经⽹络,都是以上⼀层的输出作为下⼀层的输⼊。这种⽹络被称为前馈神经⽹络。这意味着⽹络中是没有回路的 —— 信息总是向前传播,从不反向回馈。如果确实有回路,我们最终会有这样的情况:σ 函数的输⼊依赖于输出。这将难于理解,所以我们不允许这样的环路。
然⽽,也有⼀些⼈⼯神经⽹络的模型,其中反馈环路是可⾏的。这些模型被称为递归神经⽹络。这种模型的设计思想,是具有休眠前会在⼀段有限的时间内保持激活状态的神经元。这种
激活状态可以刺激其它神经元,使其随后被激活并同样保持⼀段有限的时间。这样会导致更多的神经元被激活,随着时间的推移,我们得到⼀个级联的神经元激活系统。因为⼀个神经元的
输出只在⼀段时间后⽽不是即刻影响它的输⼊,在这个模型中回路并不会引起问题。
递归神经⽹络⽐前馈⽹络影响⼒⼩得多,部分原因是递归⽹络的学习算法(⾄少⽬前为⽌)不够强⼤。但是递归⽹络仍然很有吸引⼒。它们原理上⽐前馈⽹络更接近我们⼤脑的实际⼯作。并且递归⽹络能解决⼀些重要的问题,这些问题如果仅仅⽤前馈⽹络来解决,则更加困难。然⽽为了篇幅,这里将专注于使⽤更⼴泛的前馈⽹络。








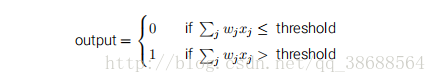
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 445
445

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








