论文原文地址:https://arxiv.org/abs/2402.03300
译文仅供大家交流学习使用,如侵权则删除。
引用请按:
arXiv:2402.03300 [cs.CL]
(or arXiv:2402.03300v3 [cs.CL] for thisversion)
https://doi.org/10.48550/arXiv.2402.03300
DeepSeekMath: 推动开放语言模型在数学推理能力上的极限
邵志宏*1,2∗†*,王培懿*1,3∗†*,朱启豪*1,3∗†*,徐润新*1*,宋俊潇*1*,毕骁*1*,张昊维*1*,张明川*1*,Y.K. Li*1*,Y. Wu*1*,郭达雅*1∗*
1DeepSeek-AI,2清华大学,3北京大学
{zhihongshao,wangpeiyi,zhuqh,guoday}@deepseek.com
https://github.com/deepseek-ai/DeepSeek-Math
摘要
数学推理因其复杂和结构化的特性,对语言模型提出了巨大的挑战。 在本文中,我们介绍了 DeepSeekMath 7B,它是在 DeepSeek-Coder-Base-v1.5 7B 的基础上,继续使用从 Common Crawl(通用网络爬虫) 抓取的 1200 亿个与数学相关的 tokens(文本单元),以及自然语言和代码数据进行预训练得到的。 DeepSeekMath 7B 在竞赛级别的 MATH 基准测试中取得了令人印象深刻的 51.7% 的成绩,且没有依赖外部工具包和投票技术,这一性能水平已接近 Gemini-Ultra 和 GPT-4。 通过对 DeepSeekMath 7B 的 64 个样本进行自洽性采样(Self-consistency),在 MATH 基准上的准确率达到了 60.9%。 DeepSeekMath 的数学推理能力归功于两个关键因素: 首先,我们通过精心设计的数据选择流程,挖掘了公开可用的网络数据的巨大潜力。 其次,我们引入了 Group Relative Policy Optimization (GRPO)(分组相对策略优化),它是 Proximal Policy Optimization (PPO)(近端策略优化)的一种变体,它在提升数学推理能力的同时,还能优化 PPO 的内存使用。

图 1: 开放源代码模型在竞赛级别 MATH 基准测试 (Hendrycks et al., 2021) 上的 Top1 准确率,测试中未使用外部工具包和投票技术。
1 介绍
大型语言模型 (LLM) 彻底革新了人工智能中数学推理的方式,极大地推动了定量推理基准测试 (Hendrycks et al., 2021) 和几何推理基准测试 (Trinh et al., 2024) 的发展。 此外,这些模型已被证明有助于人类解决复杂的数学问题 (Tao, 2023)。 然而,诸如 GPT-4 (OpenAI, 2023) 和 Gemini-Ultra (Anil et al., 2023) 等最先进的模型并非公开可用,而目前可访问的开源模型在性能上明显落后。
在本研究中,我们介绍了 DeepSeekMath,这是一种特定领域的语言模型,它在数学能力方面显著优于开源模型,并在学术基准测试中接近 GPT-4 的性能水平。 为了实现这一目标,我们创建了 DeepSeekMath Corpus,这是一个大规模、高质量的预训练语料库,包含 1200 亿个数学 tokens。 该数据集是使用基于 fastText 的分类器 (Joulin et al., 2016) 从 Common Crawl (CC) 中提取的。 在最初的迭代中,该分类器使用来自 OpenWebMath (Paster et al., 2023) 的实例作为正例进行训练,同时纳入各种其他网页作为负例。 随后,我们使用该分类器从 CC 中挖掘出更多的正例,并通过人工标注进一步提炼这些正例。 然后,使用这个增强的数据集更新分类器,以提高其性能。 评估结果表明,大规模语料库具有很高的质量,因为我们的基础模型 DeepSeekMath-Base 7B 在 GSM8K (Cobbe et al., 2021) 上取得了 64.2% 的成绩,在竞赛级别的 MATH 数据集 (Hendrycks et al., 2021) 上取得了 36.2% 的成绩, 性能优于 Minerva 540B (Lewkowycz et al., 2022a)。 此外,DeepSeekMath Corpus 是多语言的,因此我们注意到中文数学基准测试 (Wei et al., 2023; Zhong et al., 2023) 的性能也有所提升。 我们相信,我们在数学数据处理方面的经验是研究社区的一个起点,未来还有很大的改进空间。
DeepSeekMath-Base 使用 DeepSeek-Coder-Base-v1.5 7B (Guo et al., 2024) 进行初始化,因为我们注意到,与通用 LLM 相比,从代码训练模型开始是一个更好的选择。 此外,我们观察到数学训练也提高了模型在 MMLU (Hendrycks et al., 2020) 和 BBH 基准测试 (Suzgun et al., 2022) 上的能力,这表明它不仅增强了模型的数学能力,还提升了通用推理能力。
在预训练之后,我们对 DeepSeekMath-Base 应用了数学指令微调,使用了思维链 (chain-of-thought) (Wei et al., 2022)、程序思维 (program-of-thought) (Chen et al., 2022; Gao et al., 2023) 和工具集成推理 (tool-integrated reasoning) (Gou et al., 2023) 数据。 由此产生的模型 DeepSeekMath-Instruct 7B 击败了所有 7B 同类模型,并且可以与 70B 开源指令微调模型相媲美。
此外,我们还介绍了 Group Relative Policy Optimization (GRPO)(分组相对策略优化),它是近端策略优化 (Proximal Policy Optimization, PPO) (Schulman et al., 2017) 的一种变体强化学习 (RL) 算法。 GRPO 放弃了评论家模型(critic model),转而从分组得分中估计基线(baseline),从而显著减少了训练资源。 通过仅使用英语指令微调数据的一个子集,GRPO 在强大的 DeepSeekMath-Instruct 的基础上获得了显著的改进,包括在强化学习阶段的领域内 (GSM8K: 82.9% → 88.2%, MATH: 46.8% → 51.7%) 和领域外数学任务 (例如,CMATH: 84.6% → 88.8%) 性能的提升。 我们还提供了一个统一的范式来理解不同的方法,例如 Rejection Sampling Fine-Tuning (RFT) (拒绝采样微调) (Yuan et al., 2023a)、Direct Preference Optimization (DPO) (直接偏好优化) (Rafailov et al., 2023)、PPO 和 GRPO。 基于这样一个统一的范式,我们发现所有这些方法都可以概念化为直接或简化的强化学习技术。 我们还进行了广泛的实验,例如,在线与离线训练、结果与过程监督、单轮与迭代强化学习等等,以深入研究这个范式的基本要素。 最后,我们解释了为什么我们的强化学习能够提升指令微调模型的性能,并进一步总结了基于这个统一范式实现更有效的强化学习的潜在方向。
1.1 贡献
我们的贡献包括可扩展的数学预训练,以及对强化学习的探索和分析。
大规模数学预训练
-
我们的研究提供了有力的证据,表明公开可用的 Common Crawl 数据包含有价值的数学信息。 通过实施精心设计的数据选择流程,我们成功构建了 DeepSeekMath Corpus,这是一个高质量的数据集,包含从网络页面中筛选出的 1200 亿个数学内容 tokens,其规模几乎是 Minerva (Lewkowycz et al., 2022a) 使用的数学网页的 7 倍,也是最近发布的 OpenWebMath (Paster et al., 2023) 的 9 倍。
-
我们的预训练基础模型 DeepSeekMath-Base 7B 取得了与 Minerva 540B (Lewkowycz et al., 2022a) 相媲美的性能,这表明参数数量不是数学推理能力的唯一关键因素。 在高质量数据上预训练的小型模型也可以取得强大的性能。
-
我们分享了来自数学训练实验的发现。 在数学训练之前进行代码训练,可以提高模型解决数学问题的能力,无论是否使用工具。 这为长期存在的问题提供了部分答案:代码训练是否能提高推理能力? 我们认为至少对于数学推理而言,答案是肯定的。
-
尽管在 arXiv 论文上进行训练很常见,尤其是在许多与数学相关的论文中,但它并没有对本文中采用的所有数学基准测试带来显著的改进。
强化学习的探索与分析
-
我们介绍了 Group Relative Policy Optimization (GRPO)(分组相对策略优化),这是一种高效且有效的强化学习算法。 GRPO 放弃了评论家模型(critic model),转而从分组得分中估计基线(baseline),从而显著减少了与近端策略优化 (Proximal Policy Optimization, PPO) 相比的训练资源。
-
我们证明,GRPO 仅使用指令微调数据就显著提高了我们的指令微调模型 DeepSeekMath-Instruct 的性能。 此外,我们观察到在强化学习过程中,领域外性能也得到了提升。
-
我们提供了一个统一的范式来理解不同的方法,例如 RFT、DPO、PPO 和 GRPO。 我们还进行了广泛的实验,例如在线与离线训练、结果与过程监督、单轮与迭代强化学习等等,以深入研究这个范式的基本要素。
-
基于我们的统一范式,我们探索了强化学习有效性的原因,并总结了几个可以实现更有效的 LLM 强化学习的潜在方向。
1.2 评估和指标总结
-
英语和中文数学推理: 我们对我们的模型在英语和中文基准测试上进行了全面的评估,涵盖了从小学到大学水平的数学问题。 英语基准测试包括 GSM8K (Cobbe et al., 2021)、MATH (Hendrycks et al., 2021)、SAT (Azerbayev et al., 2023)、OCW Courses (Lewkowycz et al., 2022a)、MMLU-STEM (Hendrycks et al., 2020)。 中文基准测试包括 MGSM-zh (Shi et al., 2023)、CMATH (Wei et al., 2023)、Gaokao-MathCloze (Zhong et al., 2023) 和 Gaokao-MathQA (Zhong et al., 2023)。 我们评估了模型在不使用工具的情况下生成独立文本解决方案的能力,以及使用 Python 解决问题的能力。
在英语基准测试上,DeepSeekMath-Base 可以与闭源模型 Minerva 540B (Lewkowycz et al., 2022a) 相媲美,并且超越了所有开源基础模型(例如,Mistral 7B (Jiang et al., 2023) 和 Llemma-34B (Azerbayev et al., 2023)),无论它们是否经过数学预训练,通常都有显著的优势。 值得注意的是,DeepSeekMath-Base 在中文基准测试上表现更优异,这可能是因为我们没有像以前的工作 (Lewkowycz et al., 2022a; Azerbayev et al., 2023) 那样只收集英语数学预训练数据,而是也包含了高质量的非英语数据。 通过数学指令微调和强化学习,最终的 DeepSeekMath-Instruct 和 DeepSeekMath-RL 展示了强大的性能,在开源社区中首次在竞赛级别的 MATH 数据集上获得了超过 50% 的准确率。
-
形式化数学: 我们使用 (Jiang et al., 2022) 中的 informal-to-formal 定理证明任务,在 miniF2F (Zheng et al., 2021) 上评估了 DeepSeekMath-Base,并选择 Isabelle (Wenzel et al., 2008) 作为证明助手。 DeepSeekMath-Base 展示了强大的 few-shot 自动形式化(autoformalization)性能。
-
自然语言理解、推理和代码: 为了全面评估模型的一般理解、推理和编码能力,我们评估了 DeepSeekMath-Base 在 Massive Multitask Language Understanding (MMLU) 基准测试 (Hendrycks et al., 2020)、BIG-Bench Hard (BBH) (Suzgun et al., 2022) 以及 HumanEval (Chen et al., 2021) 和 MBPP (Austin et al., 2021) 上的表现。 MMLU 基准测试包含 57 个多项选择题任务,涵盖了不同的学科; BBH 由 23 个具有挑战性的任务组成,这些任务大多需要多步骤推理才能解决; HumanEval 和 MBPP 被广泛用于评估代码语言模型。 数学预训练有益于语言理解和推理性能。
2 数学预训练
2.1 数据收集与去污染
在本节中,我们将概述从 Common Crawl 构建 DeepSeekMath Corpus 的过程。 如图 2 所示,我们展示了一个迭代式流程,说明了如何从 Common Crawl 系统地收集大规模数学语料库,从种子语料库(例如,小型但高质量的数学相关数据集集合)开始。 值得注意的是,这种方法也适用于其他领域,例如代码领域。
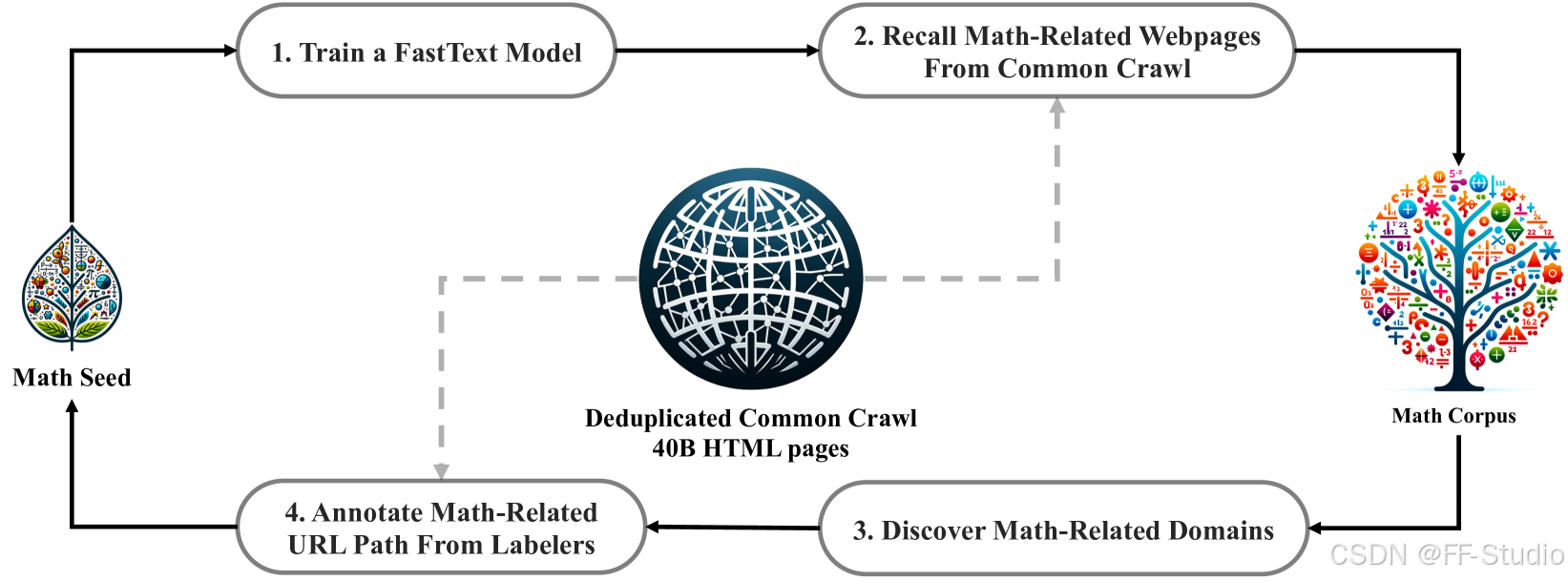
图 2: 从 Common Crawl 收集数学网页的迭代流程。
首先,我们选择 OpenWebMath (Paster et al., 2023),这是一个高质量的数学网络文本集合,作为我们的初始种子语料库。 使用这个语料库,我们训练了一个 fastText 模型 (Joulin et al., 2016),以召回更多类似 OpenWebMath 的数学网页。 具体来说,我们从种子语料库中随机选择 500,000 个数据点作为正例训练样本,并从 Common Crawl 中选择另外 500,000 个网页作为负例样本。 我们使用一个开源库1进行训练,将向量维度配置为 256,学习率配置为 0.1,单词 n-gram 的最大长度配置为 3,单词出现次数的最小值配置为 3,训练 epoch 的数量配置为 3。 为了减小原始 Common Crawl 的规模,我们采用了基于 URL 的去重和近似去重技术,最终得到了 400 亿个 HTML 网页。 然后,我们使用 fastText 模型从去重后的 Common Crawl 中召回数学网页。 为了过滤掉低质量的数学内容,我们根据 fastText 模型预测的分数对收集到的页面进行排序,并仅保留排名靠前的页面。 保留的数据量通过对前 400 亿、800 亿、1200 亿和 1600 亿 tokens 进行预训练实验来评估。 在第一次迭代中,我们选择保留前 400 亿个 tokens。
在第一次数据收集迭代之后,仍然有大量的数学网页未被收集,这主要是因为 fastText 模型是在一组缺乏足够多样性的正例样本上训练的。 因此,我们确定了额外的数学网络来源,以丰富种子语料库,从而优化 fastText 模型。 具体来说,我们首先将整个 Common Crawl 组织成不相交的域; 域被定义为共享相同基本 URL 的网页。 对于每个域,我们计算在第一次迭代中收集的网页百分比。 其中超过 10% 的网页已被收集的域被归类为与数学相关的域(例如,mathoverflow.net)。 随后,我们手动标注这些已识别域中与数学内容相关的 URL(例如,mathoverflow.net/questions)。 链接到这些 URL 但尚未收集的网页将被添加到种子语料库中。 这种方法使我们能够收集更多的正例样本,从而训练出改进的 fastText 模型,该模型能够在后续迭代中召回更多的数学数据。 经过四次数据收集迭代,我们最终获得了 3550 万个数学网页,总计 1200 亿个 tokens。 在第四次迭代中,我们注意到近 98% 的数据已经在第三次迭代中被收集,因此我们决定停止数据收集。
为了避免基准测试污染,我们遵循 Guo et al. (2024) 的方法,过滤掉包含来自英语数学基准测试(如 GSM8K (Cobbe et al., 2021) 和 MATH (Hendrycks et al., 2021))以及中文基准测试(如 CMATH (Wei et al., 2023) 和 AGIEval (Zhong et al., 2023))的问题或答案的网页。 过滤标准如下: 从我们的数学训练语料库中删除任何包含 10-gram 字符串的文本段,该字符串与评估基准测试中的任何子字符串完全匹配。 对于短于 10-gram 但至少有 3-gram 的基准测试文本,我们采用精确匹配来过滤掉受污染的网页。
2.2 验证 DeepSeekMath Corpus 的质量
我们进行了预训练实验,以研究 DeepSeekMath Corpus 与最近发布的数学训练语料库相比如何:
-
MathPile (Wang et al., 2023c): 一个多来源语料库(89 亿 tokens),汇总了教科书、维基百科、ProofWiki、CommonCrawl、StackExchange 和 arXiv,其中大部分(超过 85%)来自 arXiv;
-
OpenWebMath (Paster et al., 2023): 从 CommonCrawl 中过滤出的数学内容数据,总计 136 亿 tokens;
-
Proof-Pile-2 (Azerbayev et al., 2023): 一个数学语料库,由 OpenWebMath、AlgebraicStack(103 亿 tokens 的数学代码)和 arXiv 论文(280 亿 tokens)组成。 在 Proof-Pile-2 上进行实验时,我们遵循 Azerbayev et al. (2023) 的做法,使用 arXiv:Web:Code 的比例为 2:4:1。
2.2.1 训练设置
我们将数学训练应用于一个具有 13 亿参数的通用预训练语言模型,该模型与 DeepSeek LLMs (DeepSeek-AI, 2024) 共享相同的框架,表示为 DeepSeek-LLM 1.3B。 我们分别在每个数学语料库上训练一个模型,训练 1500 亿个 tokens。 所有实验均使用高效且轻量级的 HAI-LLM (High-flyer, 2023) 训练框架进行。 遵循 DeepSeek LLMs 的训练实践,我们使用 AdamW 优化器 (Loshchilov and Hutter, 2017),其中 β1=0.9,β2=0.95,weight_decay=0.1,以及多步学习率调整策略,其中学习率在 2,000 步 warmup 后达到峰值,在训练过程的 80% 后降至峰值的 31.6%,并在训练过程的 90% 后进一步降至峰值的 10.0%。 我们将学习率的最大值设置为 5.3e-4,并使用 4M tokens 的 batch size 和 4K 的上下文长度。
| 数学语料库 | 大小 | 英语基准测试 | 中文基准测试 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| GSM8K | MATH | OCW | SAT | MMLU-STEM | CMATH | GaokaoMathCloze | GaokaoMathQA | ||
| 无数学训练 | N/A | 2.9% | 3.0% | 2.9% | 15.6% | 19.5% | 12.3% | 0.8% | 17.9% |
| MathPile | 8.9B | 2.7% | 3.3% | 2.2% | 12.5% | 15.7% | 1.2% | 0.0% | 2.8% |
| OpenWebMath | 13.6B | 11.5% | 8.9% | 3.7% | 31.3% | 29.6% | 16.8% | 0.0% | 14.2% |
| Proof-Pile-2 | 51.9B | 14.3% | 11.2% | 3.7% | 43.8% | 29.2% | 19.9% | 5.1% | 11.7% |
| DeepSeekMath Corpus | 120.2B | 23.8% | 13.6% | 4.8% | 56.3% | 33.1% | 41.5% | 5.9% | 23.6% |
表 1: DeepSeek-LLM 1.3B 在不同数学语料库上训练后的性能,使用 few-shot 思维链 (chain-of-thought) 提示进行评估。 语料库大小是使用我们词汇量为 10 万的 tokenizer 计算得出的。

图 3: DeepSeek-LLM 1.3B 在不同数学语料库上训练的基准测试曲线。
2.2.2 评估结果
DeepSeekMath Corpus 质量高,覆盖多语言数学内容,并且规模最大。
-
高质量: 我们使用 few-shot 思维链 (chain-of-thought) 提示 Wei et al. (2022),在 8 个数学基准测试上评估了下游性能。 如表 1 所示,在 DeepSeekMath Corpus 上训练的模型具有明显的性能优势。 图 3 显示,在 500 亿 tokens 时(Proof-Pile-2 的 1 个完整 epoch),在 DeepSeekMath Corpus 上训练的模型表现出比 Proof-Pile-2 更好的性能,这表明 DeepSeekMath Corpus 的平均质量更高。
-
多语言: DeepSeekMath Corpus 包含多种语言的数据,其中英语和中文是两种最具代表性的语言。 如表 1 所示,在 DeepSeekMath Corpus 上进行训练可以提高英语和中文的数学推理性能。 相比之下,现有的数学语料库主要以英语为中心,在中文数学推理方面表现出有限的改进,甚至可能阻碍性能。
-
大规模: DeepSeekMath Corpus 比现有的数学语料库大数倍。 如图 3 所示,DeepSeek-LLM 1.3B 在 DeepSeekMath Corpus 上训练时,表现出更陡峭的学习曲线以及更持久的改进。 相比之下,基线语料库要小得多,并且在训练期间已经被重复多次,导致模型性能很快达到平台期。
2.3 训练和评估 DeepSeekMath-Base 7B
在本节中,我们介绍 DeepSeekMath-Base 7B,这是一个具有强大推理能力的基础模型,尤其是在数学方面。 我们的模型使用 DeepSeek-Coder-Base-v1.5 7B (Guo et al., 2024) 初始化,并训练了 5000 亿个 tokens。 数据分布如下: 56% 来自 DeepSeekMath Corpus,4% 来自 AlgebraicStack,10% 来自 arXiv,20% 来自 Github 代码,剩余 10% 是来自 Common Crawl 的英语和中文自然语言数据。 我们主要采用第 2.2.1 节中指定的训练设置,不同之处在于我们将学习率的最大值设置为 4.2e-4,并使用 10M tokens 的 batch size。
我们对 DeepSeekMath-Base 7B 的数学能力进行了全面评估,重点关注其在不依赖外部工具的情况下生成独立数学解决方案的能力、使用工具解决数学问题的能力以及进行形式化定理证明的能力。 除了数学之外,我们还提供了基础模型更全面的概况,包括其在自然语言理解、推理和编程技能方面的性能。
使用逐步推理解决数学问题
我们评估了 DeepSeekMath-Base 在使用 few-shot 思维链 (chain-of-thought) 提示 (Wei et al., 2022) 解决数学问题方面的性能,涵盖了英语和中文的八个基准测试。 这些基准测试包括定量推理(例如,GSM8K (Cobbe et al., 2021)、MATH (Hendrycks et al., 2021) 和 CMATH (Wei et al., 2023))和多项选择题(例如,MMLU-STEM (Hendrycks et al., 2020) 和 Gaokao-MathQA (Zhong et al., 2023)),涵盖了从小学到大学水平的复杂程度的各种数学领域。
如表 2 所示,在所有八个基准测试中,DeepSeekMath-Base 7B 在开源基础模型中均处于领先地位(包括广泛使用的通用模型 Mistral 7B (Jiang et al., 2023) 和最近发布的 Llemma 34B (Azerbayev et al., 2023),后者在 Proof-Pile-2 (Azerbayev et al., 2023) 上进行了数学训练)。 值得注意的是,在竞赛级别的 MATH 数据集上,DeepSeekMath-Base 超过了现有的开源基础模型超过 10% 的绝对值,并且优于 Minerva 540B (Lewkowycz et al., 2022a),这是一个闭源基础模型,其规模是 DeepSeekMath-Base 的 77 倍,它建立在 PaLM (Lewkowycz et al., 2022b) 的基础上,并进一步在数学文本上进行了训练。
| 模型 | 大小 | 英语基准测试 | 中文基准测试 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| GSM8K | MATH | OCW | SAT | MMLU-STEM | CMATH | GaokaoMathCloze | GaokaoMathQA | ||
| 闭源基础模型 | |||||||||
| Minerva7B | 16.2% | 14.1% | 7.7% | - | 35.6% | - | - | - | |
| Minerva62B | 52.4% | 27.6% | 12.0% | - | 53.9% | - | - | - | |
| Minerva540B | 58.8% | 33.6% | 17.6% | - | 63.9% | - | - | - | |
| 开源基础模型 | |||||||||
| Mistral7B | 40.3% | 14.3% | 9.2% | 71.9% | 51.1% | 44.9% | 5.1% | 23.4% | |
| Llemma7B | 37.4% | 18.1% | 6.3% | 59.4% | 43.1% | 43.4% | 11.9% | 23.6% | |
| Llemma34B | 54.0% | 25.3% | 10.3% | 71.9% | 52.9% | 56.1% | 11.9% | 26.2% | |
| DeepSeekMath-Base 7B | 64.2% | 36.2% | 15.4% | 84.4% | 56.5% | 71.7% | 20.3% | 35.3% |
表 2: DeepSeekMath-Base 7B 与强大的基础模型在英语和中文数学基准测试上的比较。 模型使用思维链 (chain-of-thought) 提示进行评估。 Minerva 的结果引自 Lewkowycz et al. (2022a)。
使用工具解决数学问题
我们使用 few-shot 程序思维 (program-of-thought) 提示 (Chen et al., 2022; Gao et al., 2023),在 GSM8K 和 MATH 上评估了程序辅助的数学推理能力。 模型被提示通过编写 Python 程序来解决每个问题,其中可以使用 math 和 sympy 等库进行复杂的计算。 程序的执行结果被评估为答案。 如表 3 所示,DeepSeekMath-Base 7B 优于先前的最先进模型 Llemma 34B。
| 模型 | 大小 | 使用工具解决问题 | Informal-to-Formal 证明 | ||
|---|---|---|---|---|---|
| GSM8K+Python | MATH+Python | miniF2F-valid | miniF2F-test | ||
| Mistral | 7B | 48.5% | 18.2% | 18.9% | 18.0% |
| CodeLlama | 7B | 27.1% | 17.2% | 16.3% | 17.6% |
| CodeLlama | 34B | 52.7% | 23.5% | 18.5% | 18.0% |
| Llemma | 7B | 41.0% | 18.6% | 20.6% | 22.1% |
| Llemma | 34B | 64.6% | 26.3% | 21.0% | 21.3% |
| DeepSeekMath-Base | 7B | 66.9% | 31.4% | 25.8% | 24.6% |
表 3: 基础模型使用工具解决数学问题的能力以及在 Isabelle 中进行 informal-to-formal 定理证明的能力的 few-shot 评估。
形式化数学
形式化证明自动化有利于确保数学证明的准确性和可靠性,并提高效率,近年来受到越来越多的关注。 我们在 (Jiang et al., 2022) 中的 informal-to-formal 证明任务上评估了 DeepSeekMath-Base 7B,该任务旨在基于非正式陈述、该陈述的形式化对应物和非正式证明来生成形式化证明。 我们在 miniF2F (Zheng et al., 2021) 上进行评估,这是一个用于形式化奥林匹克级别数学的基准测试,并使用 few-shot 提示为每个问题生成 Isabelle 中的形式化证明。 遵循 Jiang et al. (2022) 的方法,我们利用模型生成证明草图,并执行现成的自动定理证明器 Sledgehammer (Paulson, 2010) 来补充缺失的细节。 如表 3 所示,DeepSeekMath-Base 7B 在证明自动形式化方面表现出强大的性能。
| 模型 | 大小 | MMLU | BBH | HumanEval (Pass@1) | MBPP (Pass@1) |
|---|---|---|---|---|---|
| Mistral | 7B | 62.4% | 55.7% | 28.0% | 41.4% |
| DeepSeek-Coder-Base-v1.5† | 7B | 42.9% | 42.9% | 40.2% | 52.6% |
| DeepSeek-Coder-Base-v1.5 | 7B | 49.1% | 55.2% | 43.2% | 60.4% |
| DeepSeekMath-Base | 7B | 54.9% | 59.5% | 40.9% | 52.6% |
表 4: 在自然语言理解、推理和代码基准测试上的评估。 DeepSeek-Coder-Base-v1.5† 是学习率衰减之前的检查点,用于训练 DeepSeekMath-Base。 在 MMLU 和 BBH 上,我们使用 few-shot 思维链 (chain-of-thought) 提示。 在 HumanEval 和 MBPP 上,我们分别在 zero-shot 设置和 few-shot 设置下评估模型性能。
自然语言理解、推理和代码
我们评估了模型在 MMLU (Hendrycks et al., 2020) 上的自然语言理解性能、在 BBH (Suzgun et al., 2022) 上的推理性能以及在 HumanEval (Chen et al., 2021) 和 MBPP (Austin et al., 2021) 上的编码能力。 如表 4 所示,DeepSeekMath-Base 7B 在 MMLU 和 BBH 上的性能比其前身 DeepSeek-Coder-Base-v1.5 (Guo et al., 2024) 有显著提升,这说明数学训练对语言理解和推理的积极影响。 此外,通过包含用于持续训练的代码 tokens,DeepSeekMath-Base 7B 有效地保持了 DeepSeek-Coder-Base-v1.5 在两个代码基准测试上的性能。 总体而言,DeepSeekMath-Base 7B 在三个推理和代码基准测试上明显优于通用模型 Mistral 7B (Jiang et al., 2023)。
脚注
3 监督式微调
3.1 SFT 数据整理
我们构建了一个数学指令微调数据集,涵盖了英语和中文问题,这些问题来自不同的数学领域,难度级别也各不相同:问题与解答配对,解答形式包括思维链 (chain-of-thought, CoT) (Wei et al., 2022)、程序思维 (program-of-thought, PoT) (Chen et al., 2022; Gao et al., 2023) 以及工具集成推理格式 (tool-integrated reasoning format) (Gou et al., 2023)。 训练样本总数为 77.6 万个。
-
英语数学数据集: 我们使用工具集成的解决方案标注了 GSM8K 和 MATH 问题,并采用了 MathInstruct (Yue et al., 2023) 的一个子集以及 Lila-OOD (Mishra et al., 2022) 的训练集,在这些数据集中,问题使用 CoT 或 PoT 解决。 我们的英语数据集涵盖了不同的数学领域,例如代数、概率论、数论、微积分和几何。
-
中文数学数据集: 我们收集了中国 K-12 (中小学)数学题,涵盖 76 个子主题,例如线性方程,并使用 CoT 和工具集成推理格式标注了解答。
3.2 训练和评估 DeepSeekMath-Instruct 7B
在本节中,我们将介绍 DeepSeekMath-Instruct 7B,它是在 DeepSeekMath-Base 的基础上进行数学指令微调得到的。 训练样本被随机连接,直到达到 4K tokens 的最大上下文长度。 我们以 256 的 batch size 和 5e-5 的恒定学习率训练模型 500 步。
我们评估了模型在英语和中文的 4 个定量推理基准测试上的数学性能,包括不使用工具和使用工具两种情况。 我们将我们的模型与当时的领先模型进行了基准测试:
-
闭源模型 包括: (1) GPT 系列,其中 GPT-4 (OpenAI, 2023) 和 GPT-4 代码解释器2 是最强大的模型, (2) Gemini Ultra 和 Pro (Anil et al., 2023), (3) Inflection-2 (Inflection AI, 2023), (4) Grok-1 3, 以及中国公司最近发布的模型,包括 (5) Baichuan-3 4, (6) 来自 GLM 系列的最新 GLM-4 5 (Du et al., 2022)。 这些模型都是通用模型,其中大多数都经过了一系列对齐程序。
-
开源模型 包括: 通用模型,如 (1) DeepSeek-LLM-Chat 67B (DeepSeek-AI, 2024), (2) Qwen 72B (Bai et al., 2023), (3) SeaLLM-v2 7B (Nguyen et al., 2023), 和 (4) ChatGLM3 6B (ChatGLM3 Team, 2023), 以及数学能力增强的模型,包括 (5) InternLM2-Math 20B 6,它基于 InternLM2 构建,并进行了数学训练,然后进行了指令微调, (6) Math-Shepherd-Mistral 7B,它将 PPO 训练 (Schulman et al., 2017) 应用于 Mistral 7B (Jiang et al., 2023),并使用过程监督奖励模型, (7) WizardMath 系列 (Luo et al., 2023),它使用 evolve-instruct (即,使用 AI 进化的指令进行指令微调的一个变体) 和 PPO 训练改进了 Mistral 7B 和 Llama-2 70B (Touvron et al., 2023) 的数学推理能力,训练问题主要来自 GSM8K 和 MATH, (8) MetaMath 70B (Yu et al., 2023),它是 Llama-2 70B 在 GSM8K 和 MATH 的增强版本上进行微调得到的, (9) ToRA 34B Gou et al. (2023),它是 CodeLlama 34B 经过微调以进行工具集成数学推理得到的, (10) MAmmoTH 70B (Yue et al., 2023),它是 Llama-2 70B 在 MathInstruct 上进行指令微调得到的。
| 模型 | 大小 | 英语基准测试 | 中文基准测试 | ||
|---|---|---|---|---|---|
| GSM8K | MATH | MGSM-zh | CMATH | ||
| 思维链推理 | |||||
| 闭源模型 | |||||
| Gemini Ultra | - | 94.4% | 53.2% | – | – |
| GPT-4 | - | 92.0% | 52.9% | - | 86.0% |
| Inflection-2 | - | 81.4% | 34.8% | – | – |
| GPT-3.5 | - | 80.8% | 34.1% | - | 73.8% |
| Gemini Pro | - | 86.5% | 32.6% | – | – |
| Grok-1 | - | 62.9% | 23.9% | – | – |
| Baichuan-3 | - | 88.2% | 49.2% | – | – |
| GLM-4 | - | 87.6% | 47.9% | – | – |
| 开源模型 | |||||
| InternLM2-Math20B | 20B | 82.6% | 37.7% | – | – |
| Qwen72B | 72B | 78.9% | 35.2% | – | – |
| Math-Shepherd-Mistral7B | 7B | 84.1% | 33.0% | – | – |
| WizardMath-v1.1 7B | 7B | 83.2% | 33.0% | – | – |
| DeepSeek-LLM-Chat67B | 67B | 84.1% | 32.6% | 74.0% | 80.3% |
| MetaMath70B | 70B | 82.3% | 26.6% | 66.4% | 70.9% |
| SeaLLM-v2 7B | 7B | 78.2% | 27.5% | 64.8% | - |
| ChatGLM3 6B | 6B | 72.3% | 25.7% | – | – |
| WizardMath-v1.0 70B | 70B | 81.6% | 22.7% | 64.8% | 65.4% |
| DeepSeekMath-Instruct | 7B | 82.9% | 46.8% | 73.2% | 84.6% |
| DeepSeekMath-RL | 7B | 88.2% | 51.7% | 79.6% | 88.8% |
| 工具集成推理 | |||||
| 闭源模型 | |||||
| GPT-4 代码解释器 | - | 97.0% | 69.7% | – | – |
| 开源模型 | |||||
| InternLM2-Math20B | 20B | 80.7% | 54.3% | – | – |
| DeepSeek-LLM-Chat67B | 67B | 86.7% | 51.1% | 76.4% | 85.4% |
| ToRA34B | 34B | 80.7% | 50.8% | 41.2% | 53.4% |
| MAmmoTH70B | 70B | 76.9% | 41.8% | – | – |
| DeepSeekMath-Instruct | 7B | 83.7% | 57.4% | 72.0% | 84.3% |
| DeepSeekMath-RL | 7B | 86.7% | 58.8% | 78.4% | 87.6% |
表 5: 开放和闭源模型在英语和中文基准测试中,使用思维链和工具集成推理的性能对比。 灰色分数表示使用 32 个候选答案进行多数投票的结果; 其他为 Top1 分数。 DeepSeekMath-RL 7B 击败了所有 7B 到 70B 的开源模型,以及大多数闭源模型。 尽管 DeepSeekMath-RL 7B 仅在 GSM8K 和 MATH 的思维链格式指令微调数据上进行了进一步训练,但它在所有基准测试上都优于 DeepSeekMath-Instruct 7B。
如表 5 所示,在不允许使用工具的评估设置下,DeepSeekMath-Instruct 7B 展示了强大的逐步推理性能。 值得注意的是,在竞赛级别的 MATH 数据集上,我们的模型超越了所有开源模型和大多数专有模型(例如,Inflection-2 和 Gemini Pro)至少 9% 的绝对值。 即使对于规模明显更大的模型(例如,Qwen 72B)或通过专注于数学的强化学习进行了专门增强的模型(例如,WizardMath-v1.1 7B)也是如此。 虽然 DeepSeekMath-Instruct 在 MATH 上与中国专有模型 GLM-4 和 Baichuan-3 相当,但仍逊色于 GPT-4 和 Gemini Ultra。
在使用允许模型集成自然语言推理和基于程序的工具来解决问题的评估设置下,DeepSeekMath-Instruct 7B 在 MATH 上的准确率接近 60%,超过了所有现有的开源模型。 在其他基准测试中,我们的模型与 DeepSeek-LLM-Chat 67B (之前的最先进模型,规模是 DeepSeekMath-Instruct 7B 的 10 倍) 具有竞争力。
脚注
2 https://openai.com/blog/gpt-4-code-interpreter
3 https://x.ai/grok
4 https://platform.baichuan-ai.com/docs/api/
5 https://open.glm.cn/api_v2/dev/api
6 https://github.com/InternLM/InternLM-Math
4 强化学习
4.1 分组相对策略优化
强化学习 (RL) 已被证明在监督式微调 (SFT) 阶段之后,能有效地进一步提高大型语言模型 (LLM) 的数学推理能力 (Wang et al., 2023b; Luo et al., 2023)。 在本节中,我们将介绍我们高效且有效的强化学习算法:分组相对策略优化 (Group Relative Policy Optimization, GRPO)。
4.1.1 从 PPO 到 GRPO
近端策略优化 (Proximal Policy Optimization, PPO) (Schulman et al., 2017) 是一种 Actor-Critic (行动者-评论家) 强化学习算法,广泛应用于 LLM 的强化学习微调阶段 (Ouyang et al., 2022)。 特别是,它通过最大化以下替代目标函数来优化 LLM:
J P P O ( θ ) = E [ q ∼ P ( Q ) , o ∼ π θ o l d ( O ∣ q ) ] 1 ∥ o ∥ ∑ t = 1 ∥ o ∥ min [ π θ ( o t ∣ q , o < t ) π θ o l d ( o t ∣ q , o < t ) A t , clip ( π θ ( o t ∣ q , o < t ) π θ o l d ( o t ∣ q , o < t ) , 1 − ε , 1 + ε ) A t ] , \mathcal{J}^{PPO}(\theta)=\mathbb{E}_{[q \sim P(Q), o \sim \pi_{\theta_{old}}(O|q)]} \frac{1}{\|o\|} \sum_{t=1}^{\|o\|} \min \left[\frac{\pi_{\theta}\left(o_{t} | q, o_{<t}\right)}{\pi_{\theta_{old}}\left(o_{t} | q, o_{<t}\right)} A_{t}, \operatorname{clip}\left(\frac{\pi_{\theta}\left(o_{t} | q, o_{<t}\right)}{\pi_{\theta_{old}}\left(o_{t} | q, o_{<t}\right)}, 1-\varepsilon, 1+\varepsilon\right) A_{t}\right], JPPO(θ)=E[q∼P(Q),o∼πθold(O∣q)]∥o∥1t=1∑∥o∥min[πθold(ot∣q,o<t)πθ(ot∣q,o<t)At,clip(πθold(ot∣q,o<t)πθ(ot∣q,o<t),1−ε,1+ε)At],
其中, π θ \pi_{\theta} πθ 和 π θ o l d \pi_{\theta_{old}} πθold 分别是当前和旧的策略模型,q 和 o 分别是从问题数据集和旧策略 π θ o l d \pi_{\theta_{old}} πθold 中采样的问题和输出。 ε \varepsilon ε 是 PPO 中引入的用于稳定训练的 clipping (裁剪) 相关超参数。 A t A_t At 是优势函数 (Advantage),它通过应用广义优势估计 (Generalized Advantage Estimation, GAE) (Schulman et al., 2015) 计算得出,GAE 基于奖励 { r ≥ t } \{r_{\ge t}\} {r≥t} 和学习到的价值函数 V ψ V_{\psi} Vψ。 因此,在 PPO 中,需要与策略模型一起训练一个价值函数。 为了减轻奖励模型的过度优化,标准方法是在每个 token 的奖励中添加来自参考模型的 per-token KL 惩罚 (Ouyang et al., 2022),即:
r t = r ϕ ( q , o ≤ t ) − β log π θ ( o t ∣ q , o < t ) π r e f ( o t ∣ q , o < t ) , r_{t}=r_{\phi}\left(q, o_{\leq t}\right)-\beta \log \frac{\pi_{\theta}\left(o_{t} | q, o_{<t}\right)}{\pi_{r e f}\left(o_{t} | q, o_{<t}\right)}, rt=rϕ(q,o≤t)−βlogπref(ot∣q,o<t)πθ(ot∣q,o<t),
其中, r ϕ r_{\phi} rϕ 是奖励模型, π r e f \pi_{ref} πref 是参考模型(通常是初始的 SFT 模型), β \beta β 是 KL 惩罚的系数。

图 4: PPO 和我们的 GRPO 的演示。 GRPO 放弃了价值模型,转而从分组得分中估计基线,从而显著减少了训练资源。
由于 PPO 中使用的价值函数通常是与策略模型大小相当的另一个模型,因此它带来了大量的内存和计算负担。 此外,在强化学习训练期间,价值函数被视为优势函数计算中的基线,以减少方差。 然而在 LLM 的上下文中,通常只有最后一个 token 会被奖励模型分配一个奖励分数,这可能会使在每个 token 上都精确地训练价值函数变得复杂。 为了解决这个问题,如图 4 所示,我们提出了分组相对策略优化 (GRPO),它消除了 PPO 中对额外价值函数近似的需求,而是使用针对同一问题产生的多个采样输出的平均奖励作为基线。 更具体地说,对于每个问题 q,GRPO 从旧策略 π θ o l d \pi_{\theta_{old}} πθold 中采样一组输出 { o 1 , o 2 , ⋯ , o G } \{o_1, o_2, \cdots, o_G\} {o1,o2,⋯,oG},然后通过最大化以下目标函数来优化策略模型:
J G R P O ( θ ) = E [ q ∼ P ( Q ) , { o i } i = 1 G ∼ π θ o l d ( O ∣ q ) ] 1 G ∑ i = 1 G 1 ∥ o i ∥ ∑ t = 1 ∥ o i ∥ { min [ π θ ( o i , t ∣ q , o i , < t ) π θ o l d ( o i , t ∣ q , o i , < t ) A ^ i , t , clip ( π θ ( o i , t ∣ q , o i , < t ) π θ o l d ( o i , t ∣ q , o i , < t ) , 1 − ε , 1 + ε ) A ^ i , t ] − β D K L [ π θ ∥ π r e f ] } , \mathcal{J}^{G R P O}(\theta)=\mathbb{E}_{[q \sim P(Q), \{o_i\}_{i=1}^{G} \sim \pi_{\theta_{old}}(O|q)]} \frac{1}{G} \sum_{i=1}^{G} \frac{1}{\|o_i\|} \sum_{t=1}^{\|o_i\|} \left\{\min \left[\frac{\pi_{\theta}\left(o_{i, t} | q, o_{i,<t}\right)}{\pi_{\theta_{old}}\left(o_{i, t} | q, o_{i,<t}\right)} \hat{A}_{i, t}, \operatorname{clip}\left(\frac{\pi_{\theta}\left(o_{i, t} | q, o_{i,<t}\right)}{\pi_{\theta_{old}}\left(o_{i, t} | q, o_{i,<t}\right)}, 1-\varepsilon, 1+\varepsilon\right) \hat{A}_{i, t}\right]-\beta \mathbb{D}_{K L}\left[\pi_{\theta} \| \pi_{r e f}\right]\right\}, JGRPO(θ)=E[q∼P(Q),{oi}i=1G∼πθold(O∣q)]G1i=1∑G∥oi∥1t=1∑∥oi∥{min[πθold(oi,t∣q,oi,<t)πθ(oi,t∣q,oi,<t)A^i,t,clip(πθold(oi,t∣q,oi,<t)πθ(oi,t∣q,oi,<t),1−ε,1+ε)A^i,t]−βDKL[πθ∥πref]},
其中, ε \varepsilon ε 和 β \beta β 是超参数, A ^ i , t \hat{A}_{i,t} A^i,t 是基于仅在每个组内的输出的相对奖励计算的优势函数,这将在以下小节中详细介绍。 GRPO 用于计算优势函数的分组相对方式,与奖励模型的比较性质非常吻合,因为奖励模型通常在同一问题上输出之间的比较数据集上进行训练。 另请注意,GRPO 没有在奖励中添加 KL 惩罚,而是通过直接将训练策略和参考策略之间的 KL 散度添加到损失函数中进行正则化,避免了使 A ^ i , t \hat{A}_{i,t} A^i,t 的计算复杂化。 并且,与 (2) 中使用的 KL 惩罚项不同,我们使用以下无偏估计器 (unbiased estimator) (Schulman, 2020) 估计 KL 散度:
D K L [ π θ ∥ π r e f ] = π r e f ( o i , t ∣ q , o i , < t ) π θ ( o i , t ∣ q , o i , < t ) − log π r e f ( o i , t ∣ q , o i , < t ) π θ ( o i , t ∣ q , o i , < t ) − 1 , \mathbb{D}_{K L}\left[\pi_{\theta} \| \pi_{r e f}\right]=\frac{\pi_{r e f}\left(o_{i, t} | q, o_{i,<t}\right)}{\pi_{\theta}\left(o_{i, t} | q, o_{i,<t}\right)}-\log \frac{\pi_{r e f}\left(o_{i, t} | q, o_{i,<t}\right)}{\pi_{\theta}\left(o_{i, t} | q, o_{i,<t}\right)}-1, DKL[πθ∥πref]=πθ(oi,t∣q,oi,<t)πref(oi,t∣q,oi,<t)−logπθ(oi,t∣q,oi,<t)πref(oi,t∣q,oi,<t)−1,
这保证是正值。
算法 1 迭代式分组相对策略优化
输入: 初始策略模型 π θ i n i t \pi_{\theta_{init}} πθinit; 奖励模型 r ϕ r_{\phi} rϕ; 任务提示 D \mathcal{D} D; 超参数 ε , β , μ \varepsilon, \beta, \mu ε,β,μ
1: 初始化策略模型 π θ ← π θ i n i t \pi_{\theta} \leftarrow \pi_{\theta_{init}} πθ←πθinit
2: for 迭代次数 = 1, …, I do
3: 设置参考模型 π r e f ← π θ \pi_{ref} \leftarrow \pi_{\theta} πref←πθ
4: for 步数 = 1, …, M do
5: 从 D \mathcal{D} D 中采样一个批次 D b \mathcal{D}_b Db
6: 更新旧策略模型 π θ o l d ← π θ \pi_{\theta_{old}} \leftarrow \pi_{\theta} πθold←πθ
7: 对于 D b \mathcal{D}_b Db 中的每个问题 q,采样 G 个输出 { o i } i = 1 G ∼ π θ o l d ( ⋅ ∣ q ) \{o_i\}_{i=1}^{G} \sim \pi_{\theta_{old}}(\cdot|q) {oi}i=1G∼πθold(⋅∣q)
8: 通过运行 r ϕ r_{\phi} rϕ 计算每个采样输出 o i o_i oi 的奖励 { r i } i = 1 G \{r_i\}_{i=1}^{G} {ri}i=1G
9: 通过分组相对优势估计计算 o i o_i oi 的第 t 个 token 的 A ^ i , t \hat{A}_{i,t} A^i,t。
10: for GRPO 迭代次数 = 1, …, μ \mu μ do
11: 通过最大化 GRPO 目标函数(公式 21)更新策略模型 π θ \pi_{\theta} πθ
12: 通过使用回放机制 (replay mechanism) 的持续训练来更新 r ϕ r_{\phi} rϕ。
输出: π θ \pi_{\theta} πθ
4.1.2 基于 GRPO 的结果监督强化学习 (Outcome Supervision RL)
形式上,对于每个问题 q,从旧策略模型 π θ o l d \pi_{\theta_{old}} πθold 中采样一组输出 { o 1 , o 2 , ⋯ , o G } \{o_1, o_2, \cdots, o_G\} {o1,o2,⋯,oG}。 然后使用奖励模型对输出进行评分,从而产生 G 个相应的奖励 r = { r 1 , r 2 , ⋯ , r G } \mathbf{r}=\{r_1, r_2, \cdots, r_G\} r={r1,r2,⋯,rG}。 随后,通过减去组平均值并除以组标准差来归一化这些奖励。 结果监督在每个输出 o i o_i oi 的末尾提供归一化奖励,并将输出中所有 token 的优势函数 A ^ i , t \hat{A}_{i,t} A^i,t 设置为归一化奖励,即 A ^ i , t = r ~ i = r i − mean ( r ) std ( r ) \hat{A}_{i,t} = \tilde{r}_i = \frac{r_i - \text{mean}(\mathbf{r})}{\text{std}(\mathbf{r})} A^i,t=r~i=std(r)ri−mean(r),然后通过最大化公式 (3) 中定义的目标函数来优化策略。
4.1.3 基于 GRPO 的过程监督强化学习 (Process Supervision RL)
结果监督仅在每个输出的末尾提供奖励,这对于监督复杂数学任务中的策略可能不够充分和有效。 继 Wang et al. (2023b) 的研究,我们还探索了过程监督,它在每个推理步骤的末尾提供奖励。 形式上,给定问题 q 和 G 个采样输出 { o 1 , o 2 , ⋯ , o G } \{o_1, o_2, \cdots, o_G\} {o1,o2,⋯,oG},使用过程奖励模型对输出的每个步骤进行评分,从而产生相应的奖励: R = { { r 1 index ( 1 ) , ⋯ , r 1 index ( K 1 ) } , ⋯ , { r G index ( 1 ) , ⋯ , r G index ( K G ) } } \mathbf{R} = \{\{r_{1}^{\text{index}(1)}, \cdots, r_{1}^{\text{index}(K_1)}\}, \cdots, \{r_{G}^{\text{index}(1)}, \cdots, r_{G}^{\text{index}(K_G)}\}\} R={{r1index(1),⋯,r1index(K1)},⋯,{rGindex(1),⋯,rGindex(KG)}},其中 index ( j ) \text{index}(j) index(j) 是第 j 步的结束 token 索引, K i K_i Ki 是第 i 个输出中的总步骤数。 我们还使用平均值和标准差来归一化这些奖励,即 r ~ i index ( j ) = r i index ( j ) − mean ( R ) std ( R ) \tilde{r}_{i}^{\text{index}(j)} = \frac{r_{i}^{\text{index}(j)} - \text{mean}(\mathbf{R})}{\text{std}(\mathbf{R})} r~iindex(j)=std(R)riindex(j)−mean(R)。 随后,过程监督将每个 token 的优势函数计算为后续步骤的归一化奖励的总和,即 A ^ i , t = ∑ index ( j ) ≥ t r ~ i index ( j ) \hat{A}_{i,t} = \sum_{\text{index}(j) \ge t} \tilde{r}_{i}^{\text{index}(j)} A^i,t=∑index(j)≥tr~iindex(j),然后通过最大化公式 (3) 中定义的目标函数来优化策略。
4.1.4 基于 GRPO 的迭代强化学习
随着强化学习训练过程的进行,旧的奖励模型可能不足以监督当前的策略模型。 因此,我们还探索了基于 GRPO 的迭代强化学习。 如算法 1 所示,在迭代 GRPO 中,我们基于策略模型的采样结果为奖励模型生成新的训练集,并使用包含 10% 历史数据的回放机制持续训练旧的奖励模型。 然后,我们将参考模型设置为策略模型,并使用新的奖励模型持续训练策略模型。
4.2 训练和评估 DeepSeekMath-RL
我们基于 DeepSeekMath-Instruct 7B 进行强化学习。 强化学习的训练数据是来自 SFT 数据的与 GSM8K 和 MATH 相关的思维链格式问题,包含约 14.4 万个问题。 我们排除了其他 SFT 问题,以研究强化学习对在整个强化学习阶段都缺乏数据的基准测试的影响。 我们按照 (Wang et al., 2023b) 构建奖励模型的训练集。 我们基于 DeepSeekMath-Base 7B 训练我们的初始奖励模型,学习率为 2e-5。 对于 GRPO,我们将策略模型的学习率设置为 1e-6。 KL 系数为 0.04。 对于每个问题,我们采样 64 个输出。 最大长度设置为 1024,训练 batch size 为 1024。 策略模型在每个探索阶段后仅进行单次更新。 我们在 DeepSeekMath-Instruct 7B 之后评估 DeepSeekMath-RL 7B 在基准测试上的表现。 对于 DeepSeekMath-RL 7B,使用思维链推理的 GSM8K 和 MATH 可以被视为领域内任务,所有其他基准测试都可以被视为领域外任务。
表 5 展示了开放和闭源模型在英语和中文基准测试中使用思维链和工具集成推理的性能。 我们发现: 1) DeepSeekMath-RL 7B 在使用思维链推理的 GSM8K 和 MATH 上分别达到了 88.2% 和 51.7% 的准确率。 这一性能超过了 7B 到 70B 范围内的所有开源模型,以及大多数闭源模型。 2) 至关重要的是,DeepSeekMath-RL 7B 仅在 GSM8K 和 MATH 的思维链格式指令微调数据上进行了训练,从 DeepSeekMath-Instruct 7B 开始。 尽管其训练数据的范围有限,但它在所有评估指标上都优于 DeepSeekMath-Instruct 7B,这展示了强化学习的有效性。
5 讨论
在本节中,我们将分享我们在预训练和强化学习实验中的发现。
5.1 预训练中的经验教训
我们首先分享我们在预训练方面的经验。 除非另有说明,我们将遵循第 2.2.1 节中概述的训练设置。 值得注意的是,在本节中提到 DeepSeekMath Corpus 时,我们使用的是来自数据收集过程第二次迭代的 890 亿 tokens 的数据集。
5.1.1 代码训练有益于数学推理
一个流行但未经证实的假设表明,代码训练可以提高推理能力。 我们尝试对此提供部分解答,尤其是在数学领域: 代码训练提高了模型进行数学推理的能力,无论是否使用工具。
为了研究代码训练如何影响数学推理,我们实验了以下两种两阶段训练和一种单阶段训练设置:
两阶段训练
-
代码训练 4000 亿 tokens → 数学训练 150 亿 tokens: 我们首先对 DeepSeek-LLM 1.3B 进行 4000 亿代码 tokens 的训练,然后进行 150 亿数学 tokens 的训练;
-
通用训练 4000 亿 tokens → 数学训练 150 亿 tokens: 作为一个对照实验,我们还在第一阶段的训练中尝试使用通用 tokens(从 DeepSeek-AI 创建的大规模通用语料库中采样)代替代码 tokens,试图研究代码 tokens 在提高数学推理能力方面相对于通用 tokens 的优势。
单阶段训练
-
数学训练 150 亿 tokens: 我们对 DeepSeek-LLM 1.3B 进行 150 亿数学 tokens 的训练;
-
混合训练 4000 亿代码 tokens 和 150 亿数学 tokens: 代码训练后的数学训练会降低编码性能。 我们研究了当代码 tokens 与数学 tokens 混合进行单阶段训练时,是否仍然可以提高数学推理能力,并缓解灾难性遗忘的问题。
| 训练设置 | 训练 tokens | 不使用工具 | 使用工具 | ||
|---|---|---|---|---|---|
| 通用 | 代码 | 数学 | GSM8K | MATH | |
| 无持续训练 | — | — | — | 2.9% | 3.0% |
| 两阶段训练 | |||||
| 阶段 1:通用训练 | 400B | — | — | 2.9% | 3.2% |
| 阶段 2:数学训练 | — | — | 150B | 19.1% | 14.4% |
| 阶段 1:代码训练 | — | 400B | — | 5.9% | 3.6% |
| 阶段 2:数学训练 | — | — | 150B | 21.9% | 15.3% |
| 单阶段训练 | |||||
| 数学训练 | — | — | 150B | 20.5% | 13.1% |
| 代码和数学混合训练 | — | 400B | 150B | 17.6% | 12.1% |
表 6: 研究代码如何在不同训练设置下影响数学推理。 我们使用 DeepSeek-LLM 1.3B 进行了实验,并通过 few-shot 思维链提示和 few-shot 程序思维提示分别评估了其在不使用工具和使用工具情况下的数学推理性能。
| 训练设置 | 训练 tokens | MMLU | BBH | HumanEval (Pass@1) | MBPP (Pass@1) |
|---|---|---|---|---|---|
| 通用 | 代码 | 数学 | |||
| 无持续训练 | — | — | — | 24.5% | 28.1% |
| 两阶段训练 | |||||
| 阶段 1:通用训练 | 400B | — | — | 25.9% | 27.7% |
| 阶段 2:数学训练 | — | — | 150B | 33.1% | 32.7% |
| 阶段 1:代码训练 | — | 400B | — | 25.0% | 31.5% |
| 阶段 2:数学训练 | — | — | 150B | 36.2% | 35.3% |
| 单阶段训练 | |||||
| 数学训练 | — | — | 150B | 32.3% | 32.5% |
| 代码和数学混合训练 | — | 400B | 150B | 33.5% | 35.6% |
表 7: 研究代码和数学训练的不同设置如何影响模型在语言理解、推理和编码方面的性能。 我们使用 DeepSeek-LLM 1.3B 进行了实验。 我们使用 few-shot 思维链提示在 MMLU 和 BBH 上评估了模型。 在 HumanEval 和 MBPP 上,我们分别进行了 zero-shot 和 few-shot 评估。
结果
代码训练有益于程序辅助的数学推理,无论是在两阶段训练还是单阶段训练设置下。 如表 6 所示,在两阶段训练设置下,仅代码训练就已经显著增强了使用 Python 解决 GSM8K 和 MATH 问题的能力。 第二阶段的数学训练带来了进一步的改进。 有趣的是,在单阶段训练设置下,混合代码 tokens 和数学 tokens 有效地缓解了两阶段训练中出现的灾难性遗忘问题,并且协同增强了编码能力(表 7)和程序辅助的数学推理能力(表 6)。
代码训练还提高了不使用工具的数学推理能力。 在两阶段训练设置下,初始阶段的代码训练已经带来了适度的提升。 它还提高了后续数学训练的效率,最终带来了最佳性能。 然而,将代码 tokens 和数学 tokens 组合用于单阶段训练会损害不使用工具的数学推理能力。 一种推测是,DeepSeek-LLM 1.3B 由于其有限的规模,缺乏同时完全吸收代码和数学数据的能力。
| 模型 | 大小 | ArXiv 语料库 | 英语基准测试 | 中文基准测试 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| GSM8K | MATH | OCW | SAT | MMLU-STEM | CMATH | GaokaoMathCloze | GaokaoMathQA | |||
| DeepSeek-LLM1.3B | 无数学训练 | 2.9% | 3.0% | 2.9% | 15.6% | 19.5% | 12.3% | 0.8% | 17.9% | |
| MathPile | 2.7% | 3.3% | 2.2% | 12.5% | 15.7% | 1.2% | 0.0% | 2.8% | ||
| ArXiv-RedPajama | 3.3% | 3.4% | 4.0% | 9.4% | 9.0% | 7.4% | 0.8% | 2.3% | ||
| DeepSeek-Coder-Base-v1.5 7B | 无数学训练 | 29.0% | 12.5% | 6.6% | 40.6% | 38.1% | 45.9% | 5.9% | 21.1% | |
| MathPile | 23.6% | 11.5% | 7.0% | 46.9% | 35.8% | 37.9% | 4.2% | 25.6% | ||
| ArXiv-RedPajama | 28.1% | 11.1% | 7.7% | 50.0% | 35.2% | 42.6% | 7.6% | 24.8% |
表 8: 数学训练对不同 ArXiv 数据集的影响。 模型性能通过 few-shot 思维链提示进行评估。
| ArXiv 语料库 | miniF2F-valid | miniF2F-test |
|---|---|---|
| 无数学训练 | 20.1% | 21.7% |
| MathPile | 16.8% | 16.4% |
| ArXiv-RedPajama | 14.8% | 11.9% |
表 9: 数学训练对不同 ArXiv 语料库的影响,基础模型为 DeepSeek-Coder-Base-v1.5 7B。 我们评估了 Isabelle 中的 informal-to-formal 证明。
5.1.2 ArXiv 论文似乎在提高数学推理能力方面无效
ArXiv 论文通常被纳入作为数学预训练数据的组成部分 (Lewkowycz et al., 2022a; Polu and Sutskever, 2020; Azerbayev et al., 2023; Wang et al., 2023c)。 然而,关于它们对数学推理的影响的详细分析尚未广泛进行。 也许与直觉相反,根据我们的实验,ArXiv 论文似乎在提高数学推理能力方面无效。 我们使用不同规模的模型进行了实验,包括 DeepSeek-LLM 1.3B 和 DeepSeek-Coder-Base-v1.5 7B (Guo et al., 2024),使用了经过不同处理流程的 ArXiv 语料库:
-
MathPile (Wang et al., 2023c): 一个使用 cleaning (清理) 和 filtering (过滤) 启发式规则开发的 89 亿 tokens 的语料库,其中超过 85% 是科学 ArXiv 论文;
-
ArXiv-RedPajama (Computer, 2023): 完整的 ArXiv LaTeX 文件,移除了 preamble (导言)、注释、宏和参考文献,总计 280 亿 tokens。
在我们的实验中,我们分别在每个 ArXiv 语料库上训练了 DeepSeek-LLM 1.3B 150 亿 tokens 和 DeepSeek-Coder-Base-v1.5 7B 400 亿 tokens。 ArXiv 论文似乎在提高数学推理能力方面无效。 当仅在 ArXiv 语料库上训练时,两个模型在本文中采用的各种不同复杂度的数学基准测试中均未显示出明显的改进,甚至出现性能下降。 这些基准测试包括定量推理数据集(如 GSM8K 和 MATH,表 8)、多项选择题挑战(如 MMLU-STEM,表 8)和形式化数学(如 miniF2F,表 9)。
然而,这个结论有其局限性,应该持保留态度。 我们尚未研究:
-
• ArXiv tokens 对本研究未包含的特定数学相关任务的影响,例如定理的 informalization (非形式化),即将形式化陈述或证明转换为其非形式化版本;
-
• ArXiv tokens 与其他类型数据组合时的效果;
-
• ArXiv 论文的优势是否会在更大的模型规模上显现出来。
因此,还需要进一步探索,我们将其留待未来的研究。
5.2 强化学习的见解
5.2.1 迈向统一范式
在本节中,我们提供一个统一的范式来分析不同的训练方法,例如 SFT、RFT、DPO、PPO、GRPO,并进一步进行实验以探索统一范式的要素。 通常,训练方法关于参数 θ \theta θ 的梯度可以写成:
∇ θ J A ( θ ) = E [ ( q , o ) ∼ D ⏟ Data Source ] ( 1 ∥ o ∥ ∑ t = 1 ∥ o ∥ G C A ( q , o , t , π r f ) ⏟ Gradient Coefficient ∇ θ log π θ ( o t ∣ q , o < t ) ) . \nabla_{\theta} \mathcal{J}^{\mathcal{A}}(\theta)=\mathbb{E}_{[(q, o) \sim \mathcal{D} \underbrace{}_{\text{Data Source}}]} \left(\frac{1}{\|o\|} \sum_{t=1}^{\|o\|} \underbrace{GC^{\mathcal{A}}\left(q, o, t, \pi_{rf}\right)}_{\text{Gradient Coefficient}} \nabla_{\theta} \log \pi_{\theta}\left(o_{t} | q, o_{<t}\right)\right). ∇θJA(θ)=E[(q,o)∼DData Source ] ∥o∥1t=1∑∥o∥Gradient Coefficient GCA(q,o,t,πrf)∇θlogπθ(ot∣q,o<t) .
其中存在三个关键组成部分: 1) 数据来源 D \mathcal{D} D,它决定了训练数据; 2) 奖励函数 π r f \pi_{rf} πrf,它是训练奖励信号的来源; 3) 算法 A \mathcal{A} A: 它处理训练数据和奖励信号以获得梯度系数 G C GC GC,梯度系数决定了数据的惩罚或强化的幅度。 我们基于这样一个统一的范式分析了几种代表性方法:
| 方法 | 数据来源 | 奖励函数 | 梯度系数 |
|---|---|---|---|
| SFT | q , o ∼ P s f t ( Q , O ) q, o \sim P_{sft}(Q, O) q,o∼Psft(Q,O) | - | 1 |
| RFT | q ∼ P s f t ( Q ) , o ∼ π s f t ( O ∣ q ) q \sim P_{sft}(Q), o \sim \pi_{sft}(O|q) q∼Psft(Q),o∼πsft(O∣q) | Rule (规则) | 公式 10 |
| DPO | q ∼ P s f t ( Q ) , o + , o − ∼ π s f t ( O ∣ q ) q \sim P_{sft}(Q), o^+, o^- \sim \pi_{sft}(O|q) q∼Psft(Q),o+,o−∼πsft(O∣q) | Rule (规则) | 公式 14 |
| Online RFT | q ∼ P s f t ( Q ) , o ∼ π θ ( O ∣ q ) q \sim P_{sft}(Q), o \sim \pi_{\theta}(O|q) q∼Psft(Q),o∼πθ(O∣q) | Rule (规则) | 公式 10 |
| PPO | q ∼ P s f t ( Q ) , o ∼ π θ ( O ∣ q ) q \sim P_{sft}(Q), o \sim \pi_{\theta}(O|q) q∼Psft(Q),o∼πθ(O∣q) | Model (模型) | 公式 18 |
| GRPO | q ∼ P s f t ( Q ) , { o i } i = 1 G ∼ π θ ( O ∣ q ) q \sim P_{sft}(Q), \{o_i\}_{i=1}^G \sim \pi_{\theta}(O|q) q∼Psft(Q),{oi}i=1G∼πθ(O∣q) | Model (模型) | 公式 21 |
表 10: 不同方法的数据来源和梯度系数。 P s f t P_{sft} Psft 表示监督式微调数据集的数据分布。 π θ s f t \pi_{\theta_{sft}} πθsft 和 π θ \pi_{\theta} πθ 分别表示监督式微调模型和在线训练过程中的实时策略模型。
-
监督式微调 (SFT): SFT 在人工选择的 SFT 数据上微调预训练模型。
-
拒绝采样微调 (RFT): RFT 基于 SFT 问题,在从 SFT 模型采样的过滤输出上进一步微调 SFT 模型。 RFT 根据答案的正确性过滤输出。
-
直接偏好优化 (DPO): DPO 通过使用 pair-wise DPO 损失在从 SFT 模型采样的增强输出上对其进行微调,从而进一步优化 SFT 模型。
-
在线拒绝采样微调 (Online RFT): 与 RFT 不同,Online RFT 使用 SFT 模型初始化策略模型,并通过使用从实时策略模型采样的增强输出进行微调来优化策略模型。
-
PPO/GRPO: PPO/GRPO 使用 SFT 模型初始化策略模型,并使用从实时策略模型采样的输出对其进行强化。
我们在表 10 中总结了这些方法的组成部分。 有关更详细的推导过程,请参阅附录 A.1。

图 5: DeepSeekMath-Instruct 1.3B 模型在两种基准测试上的性能,该模型使用各种方法进行了进一步的训练。

图 6: DeepSeekMath-Instruct 7B 在两种基准测试上进行迭代强化学习的性能。
关于数据来源的观察
我们将数据来源分为两类:在线采样和离线采样。 在线采样表示训练数据来自实时训练策略模型的探索结果,而离线采样表示训练数据来自初始 SFT 模型的采样结果。 RFT 和 DPO 遵循离线风格,而 Online RFT 和 GRPO 遵循在线风格。
如图 5 所示,我们发现 Online RFT 在两个基准测试上都显著优于 RFT。 具体而言,Online RFT 在训练的早期阶段与 RFT 相当,但在后期获得了绝对优势,证明了在线训练的优越性。 这是符合直觉的,因为在初始阶段,actor (行动者) 和 SFT 模型表现出非常相似的特征,采样数据仅显示出微小的差异。 然而,在后期,从 actor 采样的数据将表现出更显着的差异,实时数据采样将提供更大的优势。
关于梯度系数的观察
该算法处理奖励信号以获得梯度系数,从而更新模型参数。 在我们的实验中,我们将奖励函数分为“规则”和“模型”两类。 规则是指基于答案的正确性来判断响应的质量,模型表示我们训练奖励模型来对每个响应进行评分。 奖励模型的训练数据基于规则判断。 公式 10 和 21 突出了 GRPO 和 Online RFT 之间的一个关键区别: GRPO 独特地根据奖励模型提供的奖励值调整其梯度系数。 这允许根据响应的不同幅度对响应进行差异化强化和惩罚。 相比之下,Online RFT 缺乏此功能; 它不会惩罚不正确的响应,并且以相同的强度统一强化所有具有正确答案的响应。
如图 5 所示,GRPO 优于 Online RFT,从而突出了改变正负梯度系数的效率。 此外,GRPO+PS 显示出比 GRPO+OS 更优越的性能,表明使用细粒度的、步骤感知的梯度系数的好处。 此外,我们探索了迭代强化学习,在我们的实验中,我们进行了两轮迭代。 如图 6 所示,我们注意到迭代强化学习显着提高了性能,尤其是在第一次迭代时。
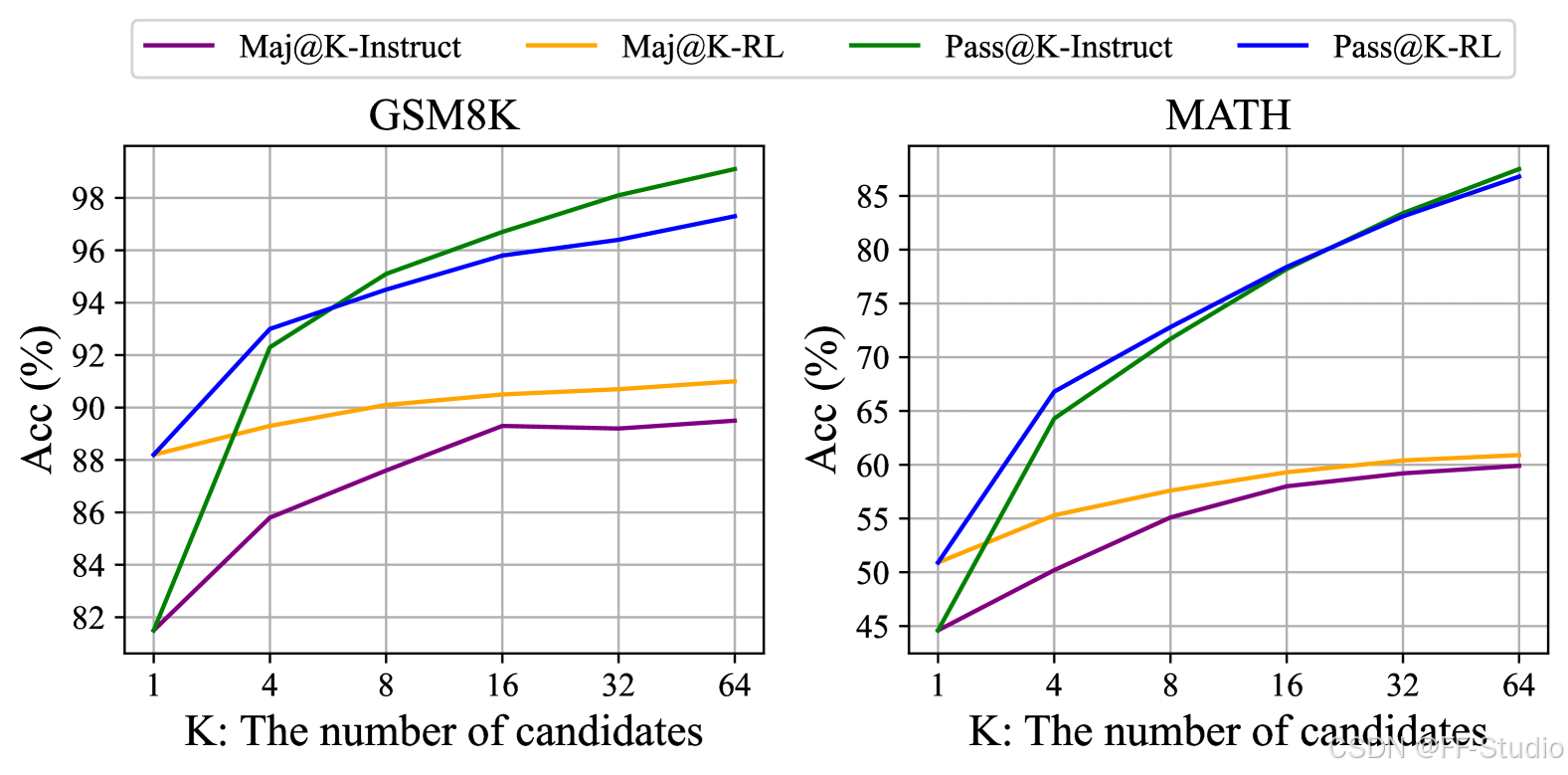
图 7: SFT 和 RL DeepSeekMath 7B 在 GSM8K 和 MATH 上的 Maj@K 和 Pass@K (温度 0.7)。 注意到 RL 增强了 Maj@K,但没有增强 Pass@K。
5.2.2 为什么强化学习有效?
在本文中,我们基于指令微调数据的一个子集进行了强化学习,并且它在指令微调模型的基础上实现了显着的性能提升。 为了进一步解释为什么强化学习有效,我们评估了 Instruct 模型和 RL 模型在两个基准测试上的 Pass@K 和 Maj@K 准确率。 如图 7 所示,RL 增强了 Maj@K 的性能,但没有增强 Pass@K。 这些发现表明,强化学习通过使输出分布更加稳健来提高模型的整体性能,换句话说,这种改进似乎归因于从 TopK 中提升正确响应,而不是增强基本能力。 类似地,(Wang et al., 2023a) 在 SFT 模型中识别出推理任务中的misalignment (未对齐) 问题,表明 SFT 模型的推理性能可以通过一系列偏好对齐策略来提高 (Yuan et al., 2023b; Song et al., 2023; Wang et al., 2023a)。
5.2.3 如何实现更有效的强化学习?
我们证明了强化学习在数学推理任务中效果很好。 我们还提供了一个统一的范式来理解不同的代表性训练方法。 在此范式中,所有方法都被概念化为直接或简化的强化学习技术。 如公式 5 总结的那样,存在三个关键组成部分:数据来源、算法和奖励函数。 我们为这三个组成部分提供了一些潜在的未来方向。
数据来源
数据来源是所有训练方法的原始材料。 在强化学习的背景下,我们特别将数据来源称为未标记的问题以及从策略模型中采样的输出。 在本文中,我们仅使用了指令微调阶段的问题和朴素的 nucleus sampling (核采样) 来采样输出。 我们认为这是我们的强化学习流程仅提高了 Maj@K 性能的潜在原因。 未来,我们将结合高级采样(解码)策略(如基于树搜索方法 (Yao et al., 2023) 的策略),探索我们的强化学习流程在 out-of-distribution (分布外) 问题提示上的应用。 此外,决定策略模型探索效率的高效推理技术 (Xia et al., 2023; Leviathan et al., 2023; Kwon et al., 2023; Xia et al., 2024) 也起着极其重要的作用。
算法
算法处理数据和奖励信号以获得梯度系数,从而更新模型参数。 在某种程度上,基于公式 5,现在所有方法都完全信任奖励函数的信号,以增加或减少某个 token 的条件概率。 然而,不可能确保奖励信号始终可靠,尤其是在极其复杂的任务中。 例如,即使是经过训练有素的标注员仔细标注的 PRM800K 数据集 (Lightman et al., 2023),仍然包含大约 20% 的错误标注7。 为此,我们将探索对噪声奖励信号具有鲁棒性的强化学习算法。 我们相信,这种 WEAK-TO-STRONG (Burns et al., 2023) 对齐方法将为学习算法带来根本性的改变。
奖励函数
奖励函数是训练信号的来源。 在强化学习中,奖励函数通常是神经奖励模型。 我们认为奖励模型存在三个重要的发展方向: 1) 如何增强奖励模型的泛化能力。 奖励模型必须有效地泛化,以处理 out-of-distribution 问题和高级解码输出; 否则,强化学习可能仅仅稳定 LLM 的分布,而不是提高其基本能力; 2) 如何反映奖励模型的不确定性。 不确定性可能会充当弱奖励模型和 weak-to-strong 学习算法之间的连接桥梁; 3) 如何高效构建高质量的过程奖励模型,从而为推理过程提供细粒度的训练信号 (Lightman et al., 2023; Wang et al., 2023b)。
脚注
7 https://huggingface.co/datasets/princeton-nlp/PRM800K
6 结论、局限性与未来工作
我们提出了 DeepSeekMath,它在竞赛级别的 MATH 基准测试中优于所有开源模型,并接近闭源模型的性能水平。 DeepSeekMath 使用 DeepSeek-Coder-v1.5 7B 初始化,并进行了 5000 亿 tokens 的持续训练,其中训练数据的重要组成部分是从 Common Crawl 抓取的 1200 亿数学 tokens。 我们广泛的消融研究表明,网页在提供高质量数学数据方面具有巨大潜力,而 arXiv 可能没有我们预期的那么有益。 我们引入了分组相对策略优化 (GRPO),它是近端策略优化 (PPO) 的一种变体,可以显著提高数学推理能力,同时减少内存消耗。 实验结果表明,即使 DeepSeekMath-Instruct 7B 在基准测试中已经达到了很高的分数,GRPO 仍然有效。 我们还提供了一个统一的范式来理解一系列方法,并总结了几个可以实现更有效的强化学习的潜在方向。
尽管 DeepSeekMath 在定量推理基准测试中取得了令人印象深刻的分数,但其在几何和定理证明方面的能力相对弱于闭源模型。 例如,在我们的初步测试中,该模型无法处理与三角形和椭圆相关的问题,这可能表明预训练和微调中存在数据选择偏差。 此外,受模型规模的限制,DeepSeekMath 在 few-shot 能力方面不如 GPT-4。 GPT-4 可以通过 few-shot 输入来提高其性能,而 DeepSeekMath 在 zero-shot 和 few-shot 评估中表现出相似的性能。 在未来,我们将进一步改进我们精心设计的数据选择流程,以构建更高质量的预训练语料库。 此外,我们将探索第 5.2.3 节中提出的潜在方向,以实现更有效的 LLM 强化学习。
参考文献
- Anil et al. (2023)↑R. Anil, S. Borgeaud, Y. Wu, J. Alayrac, J. Yu, R. Soricut, J. Schalkwyk, A. M. Dai, A. Hauth, K. Millican, D. Silver, S. Petrov, M. Johnson, I. Antonoglou, J. Schrittwieser, A. Glaese, J. Chen, E. Pitler, T. P. Lillicrap, A. Lazaridou, O. Firat, J. Molloy, M. Isard, P. R. Barham, T. Hennigan, B. Lee, F. Viola, M. Reynolds, Y. Xu, R. Doherty, E. Collins, C. Meyer, E. Rutherford, E. Moreira, K. Ayoub, M. Goel, G. Tucker, E. Piqueras, M. Krikun, I. Barr, N. Savinov, I. Danihelka, B. Roelofs, A. White, A. Andreassen, T. von Glehn, L. Yagati, M. Kazemi, L. Gonzalez, M. Khalman, J. Sygnowski, and et al.Gemini: A family of highly capable multimodal models.CoRR, abs/2312.11805, 2023.10.48550/ARXIV.2312.11805.URL https://doi.org/10.48550/arXiv.2312.11805.
- Austin et al. (2021)↑J. Austin, A. Odena, M. Nye, M. Bosma, H. Michalewski, D. Dohan, E. Jiang, C. Cai, M. Terry, Q. Le, et al.Program synthesis with large language models.arXiv preprint arXiv:2108.07732, 2021.
- Azerbayev et al. (2023)↑Z. Azerbayev, H. Schoelkopf, K. Paster, M. D. Santos, S. McAleer, A. Q. Jiang, J. Deng, S. Biderman, and S. Welleck.Llemma: An open language model for mathematics.arXiv preprint arXiv:2310.10631, 2023.
- Bai et al. (2023)↑J. Bai, S. Bai, Y. Chu, Z. Cui, K. Dang, X. Deng, Y. Fan, W. Ge, Y. Han, F. Huang, et al.Qwen technical report.arXiv preprint arXiv:2309.16609, 2023.
- Burns et al. (2023)↑C. Burns, P. Izmailov, J. H. Kirchner, B. Baker, L. Gao, L. Aschenbrenner, Y. Chen, A. Ecoffet, M. Joglekar, J. Leike, et al.Weak-to-strong generalization: Eliciting strong capabilities with weak supervision.arXiv preprint arXiv:2312.09390, 2023.
- ChatGLM3 Team (2023)↑ChatGLM3 Team.Chatglm3 series: Open bilingual chat llms, 2023.URL https://github.com/THUDM/ChatGLM3.
- Chen et al. (2021)↑M. Chen, J. Tworek, H. Jun, Q. Yuan, H. P. de Oliveira Pinto, J. Kaplan, H. Edwards, Y. Burda, N. Joseph, G. Brockman, A. Ray, R. Puri, G. Krueger, M. Petrov, H. Khlaaf, G. Sastry, P. Mishkin, B. Chan, S. Gray, N. Ryder, M. Pavlov, A. Power, L. Kaiser, M. Bavarian, C. Winter, P. Tillet, F. P. Such, D. Cummings, M. Plappert, F. Chantzis, E. Barnes, A. Herbert-Voss, W. H. Guss, A. Nichol, A. Paino, N. Tezak, J. Tang, I. Babuschkin, S. Balaji, S. Jain, W. Saunders, C. Hesse, A. N. Carr, J. Leike, J. Achiam, V. Misra, E. Morikawa, A. Radford, M. Knight, M. Brundage, M. Murati, K. Mayer, P. Welinder, B. McGrew, D. Amodei, S. McCandlish, I. Sutskever, and W. Zaremba.Evaluating large language models trained on code.CoRR, abs/2107.03374, 2021.URL https://arxiv.org/abs/2107.03374.
- Chen et al. (2022)↑W. Chen, X. Ma, X. Wang, and W. W. Cohen.Program of thoughts prompting: Disentangling computation from reasoning for numerical reasoning tasks.CoRR, abs/2211.12588, 2022.10.48550/ARXIV.2211.12588.URL https://doi.org/10.48550/arXiv.2211.12588.
- Cobbe et al. (2021)↑K. Cobbe, V. Kosaraju, M. Bavarian, M. Chen, H. Jun, L. Kaiser, M. Plappert, J. Tworek, J. Hilton, R. Nakano, et al.Training verifiers to solve math word problems.arXiv preprint arXiv:2110.14168, 2021.
- Computer (2023)↑T. Computer.Redpajama: an open dataset for training large language models, Oct. 2023.URL https://github.com/togethercomputer/RedPajama-Data.
- DeepSeek-AI (2024)↑DeepSeek-AI.Deepseek LLM: scaling open-source language models with longtermism.CoRR, abs/2401.02954, 2024.10.48550/ARXIV.2401.02954.URL https://doi.org/10.48550/arXiv.2401.02954.
- Du et al. (2022)↑Z. Du, Y. Qian, X. Liu, M. Ding, J. Qiu, Z. Yang, and J. Tang.Glm: General language model pretraining with autoregressive blank infilling.In Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 320–335, 2022.
- Gao et al. (2023)↑L. Gao, A. Madaan, S. Zhou, U. Alon, P. Liu, Y. Yang, J. Callan, and G. Neubig.PAL: program-aided language models.In A. Krause, E. Brunskill, K. Cho, B. Engelhardt, S. Sabato, and J. Scarlett, editors, International Conference on Machine Learning, ICML 2023, 23-29 July 2023, Honolulu, Hawaii, USA, volume 202 of Proceedings of Machine Learning Research, pages 10764–10799. PMLR, 2023.URL https://proceedings.mlr.press/v202/gao23f.html.
- Gou et al. (2023)↑Z. Gou, Z. Shao, Y. Gong, Y. Shen, Y. Yang, M. Huang, N. Duan, and W. Chen.Tora: A tool-integrated reasoning agent for mathematical problem solving.CoRR, abs/2309.17452, 2023.10.48550/ARXIV.2309.17452.URL https://doi.org/10.48550/arXiv.2309.17452.
- Guo et al. (2024)↑D. Guo, Q. Zhu, D. Yang, Z. Xie, K. Dong, W. Zhang, G. Chen, X. Bi, Y. Wu, Y. K. Li, F. Luo, Y. Xiong, and W. Liang.Deepseek-coder: When the large language model meets programming – the rise of code intelligence, 2024.
- Hendrycks et al. (2020)↑D. Hendrycks, C. Burns, S. Basart, A. Zou, M. Mazeika, D. Song, and J. Steinhardt.Measuring massive multitask language understanding.arXiv preprint arXiv:2009.03300, 2020.
- Hendrycks et al. (2021)↑D. Hendrycks, C. Burns, S. Kadavath, A. Arora, S. Basart, E. Tang, D. Song, and J. Steinhardt.Measuring mathematical problem solving with the math dataset.arXiv preprint arXiv:2103.03874, 2021.
- High-flyer (2023)↑High-flyer.Hai-llm: 高效且轻量的大模型训练工具, 2023.URL https://www.high-flyer.cn/en/blog/hai-llm.
- Inflection AI (2023)↑Inflection AI.Inflection-2, 2023.URL https://inflection.ai/inflection-2.
- Jiang et al. (2022)↑A. Q. Jiang, S. Welleck, J. P. Zhou, W. Li, J. Liu, M. Jamnik, T. Lacroix, Y. Wu, and G. Lample.Draft, sketch, and prove: Guiding formal theorem provers with informal proofs.arXiv preprint arXiv:2210.12283, 2022.
- Jiang et al. (2023)↑A. Q. Jiang, A. Sablayrolles, A. Mensch, C. Bamford, D. S. Chaplot, D. d. l. Casas, F. Bressand, G. Lengyel, G. Lample, L. Saulnier, et al.Mistral 7b.arXiv preprint arXiv:2310.06825, 2023.
- Joulin et al. (2016)↑A. Joulin, E. Grave, P. Bojanowski, M. Douze, H. Jégou, and T. Mikolov.Fasttext. zip: Compressing text classification models.arXiv preprint arXiv:1612.03651, 2016.
- Kwon et al. (2023)↑W. Kwon, Z. Li, S. Zhuang, Y. Sheng, L. Zheng, C. H. Yu, J. E. Gonzalez, H. Zhang, and I. Stoica.Efficient memory management for large language model serving with pagedattention.In Proceedings of the ACM SIGOPS 29th Symposium on Operating Systems Principles, 2023.
- Leviathan et al. (2023)↑Y. Leviathan, M. Kalman, and Y. Matias.Fast inference from transformers via speculative decoding.In International Conference on Machine Learning, pages 19274–19286. PMLR, 2023.
- Lewkowycz et al. (2022a)↑A. Lewkowycz, A. Andreassen, D. Dohan, E. Dyer, H. Michalewski, V. Ramasesh, A. Slone, C. Anil, I. Schlag, T. Gutman-Solo, et al.Solving quantitative reasoning problems with language models.Advances in Neural Information Processing Systems, 35:3843–3857, 2022a.
- Lewkowycz et al. (2022b)↑A. Lewkowycz, A. Andreassen, D. Dohan, E. Dyer, H. Michalewski, V. V. Ramasesh, A. Slone, C. Anil, I. Schlag, T. Gutman-Solo, Y. Wu, B. Neyshabur, G. Gur-Ari, and V. Misra.Solving quantitative reasoning problems with language models.In S. Koyejo, S. Mohamed, A. Agarwal, D. Belgrave, K. Cho, and A. Oh, editors, Advances in Neural Information Processing Systems 35: Annual Conference on Neural Information Processing Systems 2022, NeurIPS 2022, New Orleans, LA, USA, November 28 - December 9, 2022, 2022b.URL http://papers.nips.cc/paper_files/paper/2022/hash/18abbeef8cfe9203fdf9053c9c4fe191-Abstract-Conference.html.
- Lightman et al. (2023)↑H. Lightman, V. Kosaraju, Y. Burda, H. Edwards, B. Baker, T. Lee, J. Leike, J. Schulman, I. Sutskever, and K. Cobbe.Let’s verify step by step.arXiv preprint arXiv:2305.20050, 2023.
- Loshchilov and Hutter (2017)↑I. Loshchilov and F. Hutter.Decoupled weight decay regularization.arXiv preprint arXiv:1711.05101, 2017.
- Luo et al. (2023)↑H. Luo, Q. Sun, C. Xu, P. Zhao, J. Lou, C. Tao, X. Geng, Q. Lin, S. Chen, and D. Zhang.Wizardmath: Empowering mathematical reasoning for large language models via reinforced evol-instruct.arXiv preprint arXiv:2308.09583, 2023.
- Mishra et al. (2022)↑S. Mishra, M. Finlayson, P. Lu, L. Tang, S. Welleck, C. Baral, T. Rajpurohit, O. Tafjord, A. Sabharwal, P. Clark, and A. Kalyan.LILA: A unified benchmark for mathematical reasoning.In Y. Goldberg, Z. Kozareva, and Y. Zhang, editors, Proceedings of the 2022 Conference on Empirical Methods in Natural Language Processing, EMNLP 2022, Abu Dhabi, United Arab Emirates, December 7-11, 2022, pages 5807–5832. Association for Computational Linguistics, 2022.10.18653/V1/2022.EMNLP-MAIN.392.URL https://doi.org/10.18653/v1/2022.emnlp-main.392.
- Nguyen et al. (2023)↑X. Nguyen, W. Zhang, X. Li, M. M. Aljunied, Q. Tan, L. Cheng, G. Chen, Y. Deng, S. Yang, C. Liu, H. Zhang, and L. Bing.Seallms - large language models for southeast asia.CoRR, abs/2312.00738, 2023.10.48550/ARXIV.2312.00738.URL https://doi.org/10.48550/arXiv.2312.00738.
- OpenAI (2023)↑OpenAI.GPT4 technical report.arXiv preprint arXiv:2303.08774, 2023.
- Ouyang et al. (2022)↑L. Ouyang, J. Wu, X. Jiang, D. Almeida, C. Wainwright, P. Mishkin, C. Zhang, S. Agarwal, K. Slama, A. Ray, et al.Training language models to follow instructions with human feedback.Advances in Neural Information Processing Systems, 35:27730–27744, 2022.
- Paster et al. (2023)↑K. Paster, M. D. Santos, Z. Azerbayev, and J. Ba.Openwebmath: An open dataset of high-quality mathematical web text.CoRR, abs/2310.06786, 2023.10.48550/ARXIV.2310.06786.URL https://doi.org/10.48550/arXiv.2310.06786.
- Paulson (2010)↑L. C. Paulson.Three years of experience with sledgehammer, a practical link between automatic and interactive theorem provers.In R. A. Schmidt, S. Schulz, and B. Konev, editors, Proceedings of the 2nd Workshop on Practical Aspects of Automated Reasoning, PAAR-2010, Edinburgh, Scotland, UK, July 14, 2010, volume 9 of EPiC Series in Computing, pages 1–10. EasyChair, 2010.10.29007/TNFD.URL https://doi.org/10.29007/tnfd.
- Polu and Sutskever (2020)↑S. Polu and I. Sutskever.Generative language modeling for automated theorem proving.CoRR, abs/2009.03393, 2020.URL https://arxiv.org/abs/2009.03393.
- Rafailov et al. (2023)↑R. Rafailov, A. Sharma, E. Mitchell, S. Ermon, C. D. Manning, and C. Finn.Direct preference optimization: Your language model is secretly a reward model.2023.
- Schulman (2020)↑J. Schulman.Approximating kl divergence, 2020.URL http://joschu.net/blog/kl-approx.html.
- Schulman et al. (2015)↑J. Schulman, P. Moritz, S. Levine, M. Jordan, and P. Abbeel.High-dimensional continuous control using generalized advantage estimation.arXiv preprint arXiv:1506.02438, 2015.
- Schulman et al. (2017)↑J. Schulman, F. Wolski, P. Dhariwal, A. Radford, and O. Klimov.Proximal policy optimization algorithms.arXiv preprint arXiv:1707.06347, 2017.
- Shi et al. (2023)↑F. Shi, M. Suzgun, M. Freitag, X. Wang, S. Srivats, S. Vosoughi, H. W. Chung, Y. Tay, S. Ruder, D. Zhou, D. Das, and J. Wei.Language models are multilingual chain-of-thought reasoners.In The Eleventh International Conference on Learning Representations, ICLR 2023, Kigali, Rwanda, May 1-5, 2023. OpenReview.net, 2023.URL https://openreview.net/pdf?id=fR3wGCk-IXp.
- Song et al. (2023)↑F. Song, B. Yu, M. Li, H. Yu, F. Huang, Y. Li, and H. Wang.Preference ranking optimization for human alignment.arXiv preprint arXiv:2306.17492, 2023.
- Suzgun et al. (2022)↑M. Suzgun, N. Scales, N. Schärli, S. Gehrmann, Y. Tay, H. W. Chung, A. Chowdhery, Q. V. Le, E. H. Chi, D. Zhou, et al.Challenging big-bench tasks and whether chain-of-thought can solve them.arXiv preprint arXiv:2210.09261, 2022.
- Tao (2023)↑T. Tao.Embracing change and resetting expectations, 2023.URL https://unlocked.microsoft.com/ai-anthology/terence-tao/.
- Touvron et al. (2023)↑H. Touvron, L. Martin, K. Stone, P. Albert, A. Almahairi, Y. Babaei, N. Bashlykov, S. Batra, P. Bhargava, S. Bhosale, D. Bikel, L. Blecher, C. Canton-Ferrer, M. Chen, G. Cucurull, D. Esiobu, J. Fernandes, J. Fu, W. Fu, B. Fuller, C. Gao, V. Goswami, N. Goyal, A. Hartshorn, S. Hosseini, R. Hou, H. Inan, M. Kardas, V. Kerkez, M. Khabsa, I. Kloumann, A. Korenev, P. S. Koura, M. Lachaux, T. Lavril, J. Lee, D. Liskovich, Y. Lu, Y. Mao, X. Martinet, T. Mihaylov, P. Mishra, I. Molybog, Y. Nie, A. Poulton, J. Reizenstein, R. Rungta, K. Saladi, A. Schelten, R. Silva, E. M. Smith, R. Subramanian, X. E. Tan, B. Tang, R. Taylor, A. Williams, J. X. Kuan, P. Xu, Z. Yan, I. Zarov, Y. Zhang, A. Fan, M. Kambadur, S. Narang, A. Rodriguez, R. Stojnic, S. Edunov, and T. Scialom.Llama 2: Open foundation and fine-tuned chat models.CoRR, abs/2307.09288, 2023.10.48550/arXiv.2307.09288.URL https://doi.org/10.48550/arXiv.2307.09288.
- Trinh et al. (2024)↑T. H. Trinh, Y. Wu, Q. V. Le, H. He, and T. Luong.Solving olympiad geometry without human demonstrations.Nature, 625(7995):476–482, 2024.
- Wang et al. (2023a)↑P. Wang, L. Li, L. Chen, F. Song, B. Lin, Y. Cao, T. Liu, and Z. Sui.Making large language models better reasoners with alignment.arXiv preprint arXiv:2309.02144, 2023a.
- Wang et al. (2023b)↑P. Wang, L. Li, Z. Shao, R. Xu, D. Dai, Y. Li, D. Chen, Y. Wu, and Z. Sui.Math-shepherd: Verify and reinforce llms step-by-step without human annotations.CoRR, abs/2312.08935, 2023b.
- Wang et al. (2023c)↑Z. Wang, R. Xia, and P. Liu.Generative AI for math: Part I - mathpile: A billion-token-scale pretraining corpus for math.CoRR, abs/2312.17120, 2023c.10.48550/ARXIV.2312.17120.URL https://doi.org/10.48550/arXiv.2312.17120.
- Wei et al. (2022)↑J. Wei, X. Wang, D. Schuurmans, M. Bosma, B. Ichter, F. Xia, E. H. Chi, Q. V. Le, and D. Zhou.Chain-of-thought prompting elicits reasoning in large language models.In NeurIPS, 2022.URL http://papers.nips.cc/paper_files/paper/2022/hash/9d5609613524ecf4f15af0f7b31abca4-Abstract-Conference.html.
- Wei et al. (2023)↑T. Wei, J. Luan, W. Liu, S. Dong, and B. Wang.Cmath: Can your language model pass chinese elementary school math test?, 2023.
- Wenzel et al. (2008)↑M. Wenzel, L. C. Paulson, and T. Nipkow.The isabelle framework.In O. A. Mohamed, C. A. Muñoz, and S. Tahar, editors, Theorem Proving in Higher Order Logics, 21st International Conference, TPHOLs 2008, Montreal, Canada, August 18-21, 2008. Proceedings, volume 5170 of Lecture Notes in Computer Science, pages 33–38. Springer, 2008.10.1007/978-3-540-71067-7_7.URL https://doi.org/10.1007/978-3-540-71067-7_7.
- Xia et al. (2023)↑H. Xia, T. Ge, P. Wang, S.-Q. Chen, F. Wei, and Z. Sui.Speculative decoding: Exploiting speculative execution for accelerating seq2seq generation.In H. Bouamor, J. Pino, and K. Bali, editors, Findings of the Association for Computational Linguistics: EMNLP 2023, pages 3909–3925, Singapore, Dec. 2023. Association for Computational Linguistics.10.18653/v1/2023.findings-emnlp.257.URL https://aclanthology.org/2023.findings-emnlp.257.
- Xia et al. (2024)↑H. Xia, Z. Yang, Q. Dong, P. Wang, Y. Li, T. Ge, T. Liu, W. Li, and Z. Sui.Unlocking efficiency in large language model inference: A comprehensive survey of speculative decoding.arXiv preprint arXiv:2401.07851, 2024.
- Yao et al. (2023)↑S. Yao, D. Yu, J. Zhao, I. Shafran, T. L. Griffiths, Y. Cao, and K. Narasimhan.Tree of thoughts: Deliberate problem solving with large language models.arXiv preprint arXiv:2305.10601, 2023.
- Yu et al. (2023)↑L. Yu, W. Jiang, H. Shi, J. Yu, Z. Liu, Y. Zhang, J. T. Kwok, Z. Li, A. Weller, and W. Liu.Metamath: Bootstrap your own mathematical questions for large language models.CoRR, abs/2309.12284, 2023.10.48550/ARXIV.2309.12284.URL https://doi.org/10.48550/arXiv.2309.12284.
- Yuan et al. (2023a)↑Z. Yuan, H. Yuan, C. Li, G. Dong, C. Tan, and C. Zhou.Scaling relationship on learning mathematical reasoning with large language models.arXiv preprint arXiv:2308.01825, 2023a.
- Yuan et al. (2023b)↑Z. Yuan, H. Yuan, C. Tan, W. Wang, S. Huang, and F. Huang.Rrhf: Rank responses to align language models with human feedback without tears.arXiv preprint arXiv:2304.05302, 2023b.
- Yue et al. (2023)↑X. Yue, X. Qu, G. Zhang, Y. Fu, W. Huang, H. Sun, Y. Su, and W. Chen.Mammoth: Building math generalist models through hybrid instruction tuning.CoRR, abs/2309.05653, 2023.10.48550/ARXIV.2309.05653.URL https://doi.org/10.48550/arXiv.2309.05653.
- Zheng et al. (2021)↑K. Zheng, J. M. Han, and S. Polu.Minif2f: a cross-system benchmark for formal olympiad-level mathematics.arXiv preprint arXiv:2109.00110, 2021.
- Zhong et al. (2023)↑W. Zhong, R. Cui, Y. Guo, Y. Liang, S. Lu, Y. Wang, A. Saied, W. Chen, and N. Duan.AGIEval: A human-centric benchmark for evaluating foundation models.CoRR, abs/2304.06364, 2023.10.48550/arXiv.2304.06364.URL https://doi.org/10.48550/arXiv.2304.06364.
Appendix A附录
A.1 强化学习分析
我们提供了各种方法(包括 SFT、RFT、在线 RFT、DPO、PPO 和 GRPO)的数据来源和梯度系数(算法和奖励函数)的详细推导。
A.1.1 监督式微调
监督式微调的目标是最大化以下目标函数:
J S F T ( θ ) = E [ q , o ∼ P s f t ( Q , O ) ] ( 1 ∥ o ∥ ∑ t = 1 ∥ o ∥ log π θ ( o t ∣ q , o < t ) ) \mathcal{J}^{SFT}(\theta)=\mathbb{E}_{[q, o \sim P_{sft}(Q, O)]} \left(\frac{1}{\|o\|} \sum_{t=1}^{\|o\|} \log \pi_{\theta}\left(o_{t} | q, o_{<t}\right)\right) JSFT(θ)=E[q,o∼Psft(Q,O)] ∥o∥1t=1∑∥o∥logπθ(ot∣q,o<t)
J S F T ( θ ) \mathcal{J}^{SFT}(\theta) JSFT(θ) 的梯度为:
∇ θ J S F T = E [ q , o ∼ P s f t ( Q , O ) ] ( 1 ∥ o ∥ ∑ t = 1 ∥ o ∥ ∇ θ log π θ ( o t ∣ q , o < t ) ) \nabla_{\theta} \mathcal{J}^{SFT}=\mathbb{E}_{[q, o \sim P_{sft}(Q, O)]} \left(\frac{1}{\|o\|} \sum_{t=1}^{\|o\|} \nabla_{\theta} \log \pi_{\theta}\left(o_{t} | q, o_{<t}\right)\right) ∇θJSFT=E[q,o∼Psft(Q,O)] ∥o∥1t=1∑∥o∥∇θlogπθ(ot∣q,o<t)
数据来源: 用于 SFT 的数据集。
奖励函数: 可以看作是人工选择。
梯度系数: 始终设置为 1。
A.1.2 拒绝采样微调
拒绝采样微调首先为每个问题从监督式微调的 LLM 中采样多个输出,然后在具有正确答案的采样输出上训练 LLM。 形式上,RFT 的目标是最大化以下目标函数:
J R F T ( θ ) = E [ q ∼ P s f t ( Q ) , o ∼ π s f t ( O ∣ q ) ] ( 1 ∥ o ∥ ∑ t = 1 ∥ o ∥ I ( o ) log π θ ( o t ∣ q , o < t ) ) \mathcal{J}^{RFT}(\theta)=\mathbb{E}_{[q \sim P_{sft}(Q), o \sim \pi_{sft}(O|q)]} \left(\frac{1}{\|o\|} \sum_{t=1}^{\|o\|} \mathbb{I}(o) \log \pi_{\theta}\left(o_{t} | q, o_{<t}\right)\right) JRFT(θ)=E[q∼Psft(Q),o∼πsft(O∣q)] ∥o∥1t=1∑∥o∥I(o)logπθ(ot∣q,o<t)
J R F T ( θ ) \mathcal{J}^{RFT}(\theta) JRFT(θ) 的梯度为:
∇ θ J R F T ( θ ) = E [ q ∼ P s f t ( Q ) , o ∼ π s f t ( O ∣ q ) ] ( 1 ∥ o ∥ ∑ t = 1 ∥ o ∥ I ( o ) ∇ θ log π θ ( o t ∣ q , o < t ) ) \nabla_{\theta} \mathcal{J}^{RFT}(\theta)=\mathbb{E}_{[q \sim P_{sft}(Q), o \sim \pi_{sft}(O|q)]} \left(\frac{1}{\|o\|} \sum_{t=1}^{\|o\|} \mathbb{I}(o) \nabla_{\theta} \log \pi_{\theta}\left(o_{t} | q, o_{<t}\right)\right) ∇θJRFT(θ)=E[q∼Psft(Q),o∼πsft(O∣q)] ∥o∥1t=1∑∥o∥I(o)∇θlogπθ(ot∣q,o<t)
数据来源: SFT 数据集中的问题,以及从 SFT 模型采样的输出。
奖励函数: 规则(答案是否正确)。
梯度系数:
G C R F T ( q , o , t ) = I ( o ) = { 1 输出 o 的答案是正确的 0 输出 o 的答案是不正确的 GC^{RFT}(q,o,t)=\mathbb{I}(o) = \begin{cases} 1 & \text{输出 } o \text{ 的答案是正确的} \\ 0 & \text{输出 } o \text{ 的答案是不正确的} \end{cases} GCRFT(q,o,t)=I(o)={10输出 o 的答案是正确的输出 o 的答案是不正确的
A.1.3 在线拒绝采样微调
RFT 和在线 RFT 之间唯一的区别在于,在线 RFT 的输出是从实时策略模型 π θ \pi_{\theta} πθ 中采样的,而不是从 SFT 模型 π θ s f t \pi_{\theta_{sft}} πθsft 中采样的。 因此,在线 RFT 的梯度为:
∇ θ J O n R F T ( θ ) = E [ q ∼ P s f t ( Q ) , o ∼ π θ ( O ∣ q ) ] ( 1 ∥ o ∥ ∑ t = 1 ∥ o ∥ I ( o ) ∇ θ log π θ ( o t ∣ q , o < t ) ) \nabla_{\theta} \mathcal{J}^{OnRFT}(\theta)=\mathbb{E}_{[q \sim P_{sft}(Q), o \sim \pi_{\theta}(O|q)]} \left(\frac{1}{\|o\|} \sum_{t=1}^{\|o\|} \mathbb{I}(o) \nabla_{\theta} \log \pi_{\theta}\left(o_{t} | q, o_{<t}\right)\right) ∇θJOnRFT(θ)=E[q∼Psft(Q),o∼πθ(O∣q)] ∥o∥1t=1∑∥o∥I(o)∇θlogπθ(ot∣q,o<t)
A.1.4 直接偏好优化 (DPO)
DPO 的目标函数为:
J D P O ( θ ) = E [ q ∼ P s f t ( Q ) , o + , o − ∼ π s f t ( O ∣ q ) ] log σ ( β ( 1 ∥ o + ∥ ∑ t = 1 ∥ o + ∥ log π θ ( o t + ∣ q , o < t + ) π r e f ( o t + ∣ q , o < t + ) − 1 ∥ o − ∥ ∑ t = 1 ∥ o − ∥ log π θ ( o < t − ∣ q , o < t − ) π r e f ( o < t − ∣ q , o < t − ) ) ) \mathcal{J}^{DPO}(\theta)=\mathbb{E}_{[q \sim P_{sft}(Q), o^+, o^- \sim \pi_{sft}(O|q)]} \log \sigma \left(\beta \left(\frac{1}{\left\|o^+\right\|} \sum_{t=1}^{\left\|o^+\right\|} \log \frac{\pi_{\theta}\left(o_{t}^+ | q, o_{<t}^+\right)}{\pi_{ref}\left(o_{t}^+ | q, o_{<t}^+\right)} - \frac{1}{\left\|o^-\right\|} \sum_{t=1}^{\left\|o^-\right\|} \log \frac{\pi_{\theta}\left(o_{<t}^- | q, o_{<t}^-\right)}{\pi_{ref}\left(o_{<t}^- | q, o_{<t}^-\right)}\right)\right) JDPO(θ)=E[q∼Psft(Q),o+,o−∼πsft(O∣q)]logσ β ∥o+∥1t=1∑∥o+∥logπref(ot+∣q,o<t+)πθ(ot+∣q,o<t+)−∥o−∥1t=1∑∥o−∥logπref(o<t−∣q,o<t−)πθ(o<t−∣q,o<t−)
J D P O ( θ ) \mathcal{J}^{DPO}(\theta) JDPO(θ) 的梯度为:
∇ θ J D P O ( θ ) = E [ q ∼ P s f t ( Q ) , o + , o − ∼ π s f t ( O ∣ q ) ] ( 1 ∥ o + ∥ ∑ t = 1 ∥ o + ∥ G C D P O ( q , o , t ) ∇ θ log π θ ( o t + ∣ q , o < t + ) − 1 ∥ o − ∥ ∑ t = 1 ∥ o − ∥ G C D P O ( q , o , t ) ∇ θ log π θ ( o t − ∣ q , o < t − ) ) \nabla_{\theta} \mathcal{J}^{DPO}(\theta)=\mathbb{E}_{[q \sim P_{sft}(Q), o^+, o^- \sim \pi_{sft}(O|q)]} \left(\frac{1}{\left\|o^+\right\|} \sum_{t=1}^{\left\|o^+\right\|} GC^{DPO}(q,o,t) \nabla_{\theta} \log \pi_{\theta}\left(o_{t}^+ | q, o_{<t}^+\right) - \frac{1}{\left\|o^-\right\|} \sum_{t=1}^{\left\|o^-\right\|} GC^{DPO}(q,o,t) \nabla_{\theta} \log \pi_{\theta}\left(o_{t}^- | q, o_{<t}^-\right)\right) ∇θJDPO(θ)=E[q∼Psft(Q),o+,o−∼πsft(O∣q)] ∥o+∥1t=1∑∥o+∥GCDPO(q,o,t)∇θlogπθ(ot+∣q,o<t+)−∥o−∥1t=1∑∥o−∥GCDPO(q,o,t)∇θlogπθ(ot−∣q,o<t−)
数据来源: SFT 数据集中的问题,以及从 SFT 模型采样的输出。
奖励函数: 通用领域中的人类偏好(在数学任务中可以是“规则”)。
梯度系数:
G C D P O ( q , o , t ) = σ ( β ( log π θ ( o t − ∣ q , o < t − ) π r e f ( o t − ∣ q , o < t − ) − log π θ ( o t + ∣ q , o < t + ) π r e f ( o t + ∣ q , o < t + ) ) ) GC^{DPO}(q,o,t)=\sigma \left(\beta \left(\log \frac{\pi_{\theta}\left(o_{t}^- | q, o_{<t}^-\right)}{\pi_{ref}\left(o_{t}^- | q, o_{<t}^-\right)} - \log \frac{\pi_{\theta}\left(o_{t}^+ | q, o_{<t}^+\right)}{\pi_{ref}\left(o_{t}^+ | q, o_{<t}^+\right)}\right)\right) GCDPO(q,o,t)=σ(β(logπref(ot−∣q,o<t−)πθ(ot−∣q,o<t−)−logπref(ot+∣q,o<t+)πθ(ot+∣q,o<t+)))
A.1.5 近端策略优化 (PPO)
PPO 的目标函数为:
J P P O ( θ ) = E [ q ∼ P s f t ( Q ) , o ∼ π θ o l d ( O ∣ q ) ] 1 ∥ o ∥ ∑ t = 1 ∥ o ∥ min [ π θ ( o t ∣ q , o < t ) π θ o l d ( o t ∣ q , o < t ) A t , clip ( π θ ( o t ∣ q , o < t ) π θ o l d ( o t ∣ q , o < t ) , 1 − ε , 1 + ε ) A t ] \mathcal{J}^{PPO}(\theta)=\mathbb{E}_{[q \sim P_{sft}(Q), o \sim \pi_{\theta_{old}}(O|q)]} \frac{1}{\|o\|} \sum_{t=1}^{\|o\|} \min \left[\frac{\pi_{\theta}\left(o_{t} | q, o_{<t}\right)}{\pi_{\theta_{old}}\left(o_{t} | q, o_{<t}\right)} A_{t}, \operatorname{clip}\left(\frac{\pi_{\theta}\left(o_{t} | q, o_{<t}\right)}{\pi_{\theta_{old}}\left(o_{t} | q, o_{<t}\right)}, 1-\varepsilon, 1+\varepsilon\right) A_{t}\right] JPPO(θ)=E[q∼Psft(Q),o∼πθold(O∣q)]∥o∥1t=1∑∥o∥min[πθold(ot∣q,o<t)πθ(ot∣q,o<t)At,clip(πθold(ot∣q,o<t)πθ(ot∣q,o<t),1−ε,1+ε)At]
为了简化分析,假设模型在每个探索阶段之后仅进行单次更新,从而确保 π θ o l d = π θ \pi_{\theta_{old}}=\pi_{\theta} πθold=πθ。 在这种情况下,我们可以移除 min 和 clip 操作:
J P P O ( θ ) = E [ q ∼ P s f t ( Q ) , o ∼ π θ o l d ( O ∣ q ) ] 1 ∥ o ∥ ∑ t = 1 ∥ o ∥ π θ ( o t ∣ q , o < t ) π θ o l d ( o t ∣ q , o < t ) A t \mathcal{J}^{PPO}(\theta)=\mathbb{E}_{[q \sim P_{sft}(Q), o \sim \pi_{\theta_{old}}(O|q)]} \frac{1}{\|o\|} \sum_{t=1}^{\|o\|} \frac{\pi_{\theta}\left(o_{t} | q, o_{<t}\right)}{\pi_{\theta_{old}}\left(o_{t} | q, o_{<t}\right)} A_{t} JPPO(θ)=E[q∼Psft(Q),o∼πθold(O∣q)]∥o∥1t=1∑∥o∥πθold(ot∣q,o<t)πθ(ot∣q,o<t)At
J P P O ( θ ) \mathcal{J}^{PPO}(\theta) JPPO(θ) 的梯度为:
∇ θ J P P O ( θ ) = E [ q ∼ P s f t ( Q ) , o ∼ π θ o l d ( O ∣ q ) ] 1 ∥ o ∥ ∑ t = 1 ∥ o ∥ A t ∇ θ log π θ ( o t ∣ q , o < t ) \nabla_{\theta} \mathcal{J}^{PPO}(\theta)=\mathbb{E}_{[q \sim P_{sft}(Q), o \sim \pi_{\theta_{old}}(O|q)]} \frac{1}{\|o\|} \sum_{t=1}^{\|o\|} A_{t} \nabla_{\theta} \log \pi_{\theta}\left(o_{t} | q, o_{<t}\right) ∇θJPPO(θ)=E[q∼Psft(Q),o∼πθold(O∣q)]∥o∥1t=1∑∥o∥At∇θlogπθ(ot∣q,o<t)
数据来源: SFT 数据集中的问题,以及从策略模型采样的输出。
奖励函数: 奖励模型。
梯度系数:
G C P P O ( q , o , t , π θ r m ) = A t , GC^{PPO}(q,o,t,\pi_{\theta}^{rm})=A_t, GCPPO(q,o,t,πθrm)=At,
其中 A t A_t At 是优势函数,它通过应用广义优势估计 (GAE) (Schulman et al., 2015) 计算得出,GAE 基于奖励 { r ≥ t } \{r_{\ge t}\} {r≥t} 和学习到的价值函数 V ψ V_{\psi} Vψ。
A.1.6 分组相对策略优化 (GRPO)
GRPO 的目标函数为(假设 π θ o l d = π θ \pi_{\theta_{old}}=\pi_{\theta} πθold=πθ 以简化分析):
J G R P O ( θ ) = E [ q ∼ P s f t ( Q ) , { o i } i = 1 G ∼ π θ o l d ( O ∣ q ) ] 1 G ∑ i = 1 G 1 ∥ o i ∥ ∑ t = 1 ∥ o i ∥ [ π θ ( o i , t ∣ q , o i , < t ) π θ o l d ( o i , t ∣ q , o i , < t ) A ^ i , t − β ( π r e f ( o i , t ∣ q , o i , < t ) π θ ( o i , t ∣ q , o i , < t ) − log π r e f ( o i , t ∣ q , o i , < t ) π θ ( o i , t ∣ q , o i , < t ) − 1 ) ] \mathcal{J}^{GRPO}(\theta)=\mathbb{E}_{[q \sim P_{sft}(Q), \{o_i\}_{i=1}^G \sim \pi_{\theta_{old}}(O|q)]} \frac{1}{G} \sum_{i=1}^G \frac{1}{\|o_i\|} \sum_{t=1}^{\|o_i\|} \left[\frac{\pi_{\theta}\left(o_{i, t} | q, o_{i,<t}\right)}{\pi_{\theta_{old}}\left(o_{i, t} | q, o_{i,<t}\right)} \hat{A}_{i, t} - \beta \left(\frac{\pi_{ref}\left(o_{i, t} | q, o_{i,<t}\right)}{\pi_{\theta}\left(o_{i, t} | q, o_{i,<t}\right)} - \log \frac{\pi_{ref}\left(o_{i, t} | q, o_{i,<t}\right)}{\pi_{\theta}\left(o_{i, t} | q, o_{i,<t}\right)} - 1\right)\right] JGRPO(θ)=E[q∼Psft(Q),{oi}i=1G∼πθold(O∣q)]G1i=1∑G∥oi∥1t=1∑∥oi∥[πθold(oi,t∣q,oi,<t)πθ(oi,t∣q,oi,<t)A^i,t−β(πθ(oi,t∣q,oi,<t)πref(oi,t∣q,oi,<t)−logπθ(oi,t∣q,oi,<t)πref(oi,t∣q,oi,<t)−1)]
J G R P O ( θ ) \mathcal{J}^{GRPO}(\theta) JGRPO(θ) 的梯度为:
∇ θ J G R P O ( θ ) = E [ q ∼ P s f t ( Q ) , { o i } i = 1 G ∼ π θ o l d ( O ∣ q ) ] 1 G ∑ i = 1 G 1 ∥ o i ∥ ∑ t = 1 ∥ o i ∥ [ A ^ i , t + β ( π r e f ( o i , t ∣ o i , < t ) π θ ( o i , t ∣ o i , < t ) − 1 ) ] ∇ θ log π θ ( o i , t ∣ q , o i , < t ) \nabla_{\theta} \mathcal{J}^{GRPO}(\theta)=\mathbb{E}_{[q \sim P_{sft}(Q), \{o_i\}_{i=1}^G \sim \pi_{\theta_{old}}(O|q)]} \frac{1}{G} \sum_{i=1}^G \frac{1}{\|o_i\|} \sum_{t=1}^{\|o_i\|} \left[\hat{A}_{i, t} + \beta \left(\frac{\pi_{ref}\left(o_{i, t} | o_{i,<t}\right)}{\pi_{\theta}\left(o_{i, t} | o_{i,<t}\right)} - 1\right)\right] \nabla_{\theta} \log \pi_{\theta}\left(o_{i, t} | q, o_{i,<t}\right) ∇θJGRPO(θ)=E[q∼Psft(Q),{oi}i=1G∼πθold(O∣q)]G1i=1∑G∥oi∥1t=1∑∥oi∥[A^i,t+β(πθ(oi,t∣oi,<t)πref(oi,t∣oi,<t)−1)]∇θlogπθ(oi,t∣q,oi,<t)
数据来源: SFT 数据集中的问题,以及从策略模型采样的输出。
奖励函数: 奖励模型。
梯度系数:
G C G R P O ( q , o , t , π θ r m ) = A ^ i , t + β ( π r e f ( o i , t ∣ o i , < t ) π θ ( o i , t ∣ o i , < t ) − 1 ) , GC^{GRPO}(q,o,t,\pi_{\theta}^{rm})=\hat{A}_{i, t} + \beta \left(\frac{\pi_{ref}\left(o_{i, t} | o_{i,<t}\right)}{\pi_{\theta}\left(o_{i, t} | o_{i,<t}\right)} - 1\right), GCGRPO(q,o,t,πθrm)=A^i,t+β(πθ(oi,t∣oi,<t)πref(oi,t∣oi,<t)−1),
其中 A ^ i , t \hat{A}_{i,t} A^i,t 基于分组奖励分数计算得出。

























 1513
1513

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








