＜论文阅读＞Inertial-Only Optimization for Visual-Inertial Initialization

我们工作的主要贡献是:

1. 考虑IMU噪声的概率模型的情况下，将视觉-惯性初始化问题表述为只考虑惯性的最优估计问题。
2. 我们一次性求解了所有的惯性参数，避免了解耦估计所产生的不一致性。这使得所有的估计都一致。
3. 我们不做任何初始速度和姿态的假设，这使得我们的方法适用于任何初始情况。
4. 我们不假设IMU偏差为零，相反，我们将它们的已知信息编码为被我们的MAP估计所利用的概率先验。

---

最大后验初始化 MAP（maximum-a-posteriori）

适当考虑了所有传感器的噪声特性，得到了所有变量的最大后验联合估计。由于其强烈的非线性特性，VI-BA（visual-inertial bundle adjustment）算法主要局限性是需要一个好的种子来快速收敛，避免陷入局部极小值。基于最小二乘估计的联合和不联合初始化方法表明，VI-BA极大地改善了它们的初始解。

我们的主要目标是更进一步，在初始化时也使用MAP估算，正确使用传感器噪声模型。
我们的新初始化方法基于以下思想:

• 尽管BA是非线性的，单目SLAM是成熟的且是足以获得非常精确的运动初始值的解决方案，但是其测量值是缺少尺度的。
• 视觉SLAM轨迹的不确定性比IMU的不确定性小得多，可以在IMU变量的第一次求解时忽略不计。因此，我们只执行惯性MAP估计，以缺少尺度的视觉SLAM轨迹为常数
• 我们采用了一种参数化方法来明确地表示和优化单目SLAM尺度的解决方案。
• 我们在一个步骤同时优化所有的IMU变量，考虑位置，线速度和角速度积分项之间的的交叉协方差。

我们的初始化方法可以分为三个步骤:

1. Vision-only MAP estimation：使用BA初始化并运行短时间(通常是2秒)的单目ORB-SLAM，以获得一个纯视觉MAP估算的 up-to-scale。同时，计算关键帧间的IMU预积分及其协方差。
2. Inertial-only MAP estimation：仅针对惯性的优化，使IMU轨迹与ORB-SLAM轨迹对齐，找到尺度，关键帧的速度、重力方向和IMU偏差 biases。
3. Visual-inertial MAP estimation：将上一步的解作为完整VI-BA的种子，得到联合最优解。

---

1. Vision-only MAP estimation

我们初始化纯单目SLAM，使用与ORB-SLAM相同的程序来寻找初始运动。在两个初始帧之间使用ORB描述符进行快速点匹配，建立了基本矩阵和单应性模型并进行了评分，得分较高的一种用于寻找初始运动并对特征进行三角化处理。

与ORB-SLAM的唯一区别是，我们以更高的频率强制关键帧插入(4 Hz ~ 10 Hz)，因为积分时间很短，IMU在关键帧之间的预积分具有较低的不确定性。在这段时间之后，我们会有一个由10个关键帧和数百个点组成的缺少尺度的地图，它们都已经经过BA优化。

使用视觉IMU校准，将缺少尺度的关键帧姿态转换到body(或IMU)参考系下。这些body坐标系下的位姿被定义为${\bar{T}}_{0:k}=[R,\bar{p}{]}_{0:k}$，这里的$R_i\in SO(3)$是从第$i$个body坐标系到world坐标系的旋转矩阵，${\bar{p}}_i\in {\mathbb{R}}^3$是在第$i$个body坐标系下的无尺度位置。

---

2. Inertial-only MAP Estimation

这一步的目标是获得IMU参数的最优估计，从MAP估计的意义上来说，利用上一步视觉得到的无尺度上的轨迹。因为我们无法很好的猜测IMU的参数作为VI-BA的初值，因为其容易陷入局部最小值。

折中的解决方案是边缘化点（仅仅使用其带来的变量,不参与优化过程），以获得一个先验的轨迹，和它的(完全稠密)协方差矩阵，并在优化IMU参数时使用它。

我们选择了一个更有效的解决方案，认为轨迹位姿是固定的，执行一个纯IMU的优化。要找到的惯性参数为:
X k = { s , R w g , b , v ˉ 0 : k } \mathcal X_k = \{s,R_{wg},b,\bar{v}_{0:k}\} Xk​={s,Rwg​,b,vˉ0:k​}其中$s\in {\mathbb{R}}^3$是纯视觉中的尺度因子，$R_{wg}\in SO(3)$是重力方向，$b=(b^a,b^g)\in {\mathbb{R}}^6$是加速度和角速度的偏差，${\bar{v}}_{0:k}\in {\mathbb{R}}^3$代表在body坐标系下每一帧无尺度的速度。

我们更喜欢使用无尺度的速度${\bar{v}}_i$，而不是真实速度$v_i=s{\bar{v}}_i$，因为它的初始化过程更加简单。：由于初始化过程仅为1-2秒，且随机噪声几乎没有影响，所以所有关键帧的偏差都被假定为常量。

我们定义${\mathcal{L}}_{i,j}$为IMU从第$i$帧到第$j$帧之间的预积分，${\mathcal{L}}_{0,k}$表示在初始化窗口的连续关键帧之间的预积分。
有了定义的状态和测量值，我们可以制定一个MAP估计问题，其中后验分布是：
$$p({\mathcal{X}}_k|{\mathcal{L}}_{0:k})\propto p({\mathcal{L}}_{0,k}|{\mathcal{X}}_k)p({\mathcal{X}}_k)$$其中，$p({\mathcal{L}}_{0,k}|{\mathcal{X}}_k)$表示在给定第k帧IMU数据的情况下, 从0到k帧的可能的IMU测量值分布可能性。$p({\mathcal{X}}_k)$为IMU状态的先验。考虑到测量值之间相互独立，可以将其分解为:$$p({\mathcal{L}}_{0:k}|{\mathcal{X}}_k)=\prod _{i=1}^k(p({\mathcal{L}}_{i-1,i}|s,g_{dir},b,v_{i-1},v_i))$$我们需要找到参数使后验概率最大，意味着使其负对数的值更小：$${\mathcal{X}}_k^{\ast }=arg\underset{{\mathcal{X}}_k}{\max }p({\mathcal{X}}_k|{\mathcal{L}}_{0:k})=arg\underset{{\mathcal{X}}_k}{\min }(-log(p({\mathcal{X}}_k))-\sum _{i=1}^{k}log(p({\mathcal{L}}_{i-1,i}|s,g_{dir},b,v_{i-1},v_i)))$$因为假设IMU的预积分都是服从高斯分布的，则MAP问题等价于：
$${\mathcal{X}}_k^{\ast }=arg\underset{{\mathcal{X}}_k}{\min }\left(\Vert r_p{\Vert }_{{\sum }_p}^2+\sum _{i+1}^k\Vert r_{{\mathcal{L}}_{i-1,i}}{\Vert }_{{\sum }_{{\mathcal{L}}_{i-1,i}}}^2\right)$$其中，$r_p$和$r_{{\mathcal{L}}_{i-1,i}}$为先验值和IMU测量值的残差，而${\sum }_p$和${\sum }_{{\mathcal{L}}_{i-1,i}}$为他们的协方差。
在本次优化的过程中，不在考虑视觉投影误差，只有IMU的误差。因为其相互独立，使用robust核函数是没有意义的，反而会减慢优化速度。我们定义旋转矩阵，速度，位移的误差如下：
$$r_{{\mathcal{L}}_{i-1,i}}=[r_{\Delta R_{i,j}},r_{\Delta v_{i,j}},r_{\Delta p_{i,j}}]$$详情可参考<VIO残差函数的构建以及IMU预积分和协方差传递>

众所周知，在文献中，重力和加速度计的偏差往往是耦合的，在大多数情况下很难区分。为了避免这个问题，一些技术在初始化过程中忽略了加速度计的偏差，假设为零值。而另一些技术则等待很长时间来保证它是可观察到的。在ORBSLAM3的IMU相关公式中，并没有随机游走，且在两个关键帧之间，偏差bias为常数。

在这方面，我们采取了稳健的方法：我们将$b^a$作为需要优化的参数，添加了其先验误差，$r_p=\Vert b^a{\Vert }_{{\sum }_p}^2$，如果运动时没有足够的信息去估计该偏差，其先验会保证他的测量值接近于0，如果运动使得$b^a$可被观察到，则其测量值会逐渐趋近于真值。$b^g$的先验是不需要的，因为他可以很好的在关键帧的方向角上得到，也可以从陀螺仪上读到。

因为我们需要解决一个非线性优化问题，因此需要一个惯性参数的初始值。因此我们初始化偏差等于0，然而重力方向是沿着加速度计的平均值初始化的，加速度值通常要比重力更小。

尺度因子需要初始化得足够接近它的真值才能保证收敛，但是我们并没有初始的估计。考虑到纯IMU的优化优点(5ms)，我们同时启动3个初始尺度的优化，对应的中值深度分别为1,4和16米，按照残差定义保留最小的残差方案。我们的结果表明，使用这个尺度值范围，我们的方法能够在广泛的场景中收敛。在优化结束时，帧位和速度和3D地图点将根据找到的尺度进行缩放，并旋转以使z轴与估计的重力方向对齐，用新的偏置bias重复估计IMU预积分，可以减少未来的线性化误差。

---

3. Visual-Inertial MAP Estimation

纯惯性优化提供了一种足够精确的估计，可作为第一次视觉-惯性BA的初值，确保其收敛。重力加速度和尺度并不会被直接优化，因为他们隐藏在关键帧的pose中。

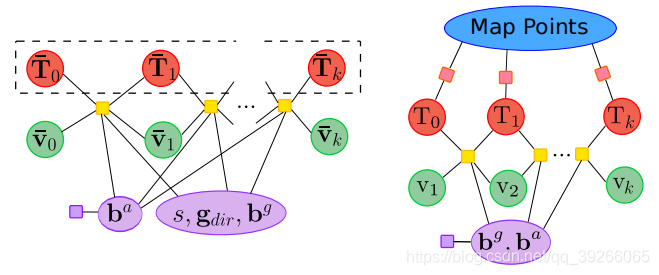
相比较《Fast and robust initialization for visual-inertial SLAM》，此步骤取代BA1&2步骤。事实上，优化是完全一样的，只不过先前是求解一个线性化系统，而现在是一个MAP求解问题，初始值不同。

我们注意到，所有初始化步骤都是在一个并行线程中执行的，不会对实时跟踪线程产生任何影响。一旦优化完成，系统已经初始化，将从视觉SLAM转向视觉-惯性SLAM。