决策树算法中基尼指数与信息增益的比较

最新推荐文章于 2025-08-29 08:29:53 发布

原创

最新推荐文章于 2025-08-29 08:29:53 发布 · 6.6k 阅读

28 ·

CC 4.0 BY-SA版权

文章标签：

#决策树 #基尼指数 #信息增益 #数据挖掘

问题提出

在自己实现决策树算法的时候，发现生成的id3树和cart树一模一样。竟然每个决策节点都选择了同一属性的同一划分。这让我很意外，于是改变了随机种子值，改变训练集的大小，结果发现无一例外它们都是一样的。由此我提出了一个疑问：基尼指数和信息增益是等价的吗？
如果等价，那干嘛还要两个算法？如果不等价，为什么生成的树总是一样的呢？

二者比较

直接取iris数据集中的一部分作为训练集，并指定一个属性作为判断标准。列出一系列对该属性的划分，同时用基尼指数和信息增益作为判断标准进行评价，以此比较两者的区别（此例中训练集大小为100个样本，对0号属性“sepal length”进行划分）
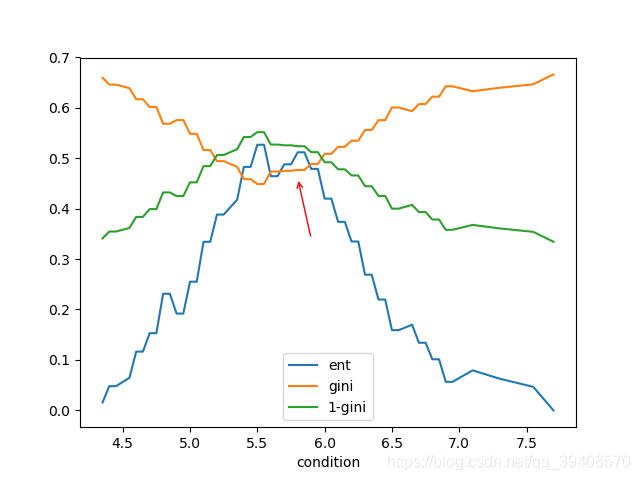
基尼指数vs信息增益
ent为信息增益，gini为基尼指数。同时为了便于观察，引入了 $1 - g i n i$ ，这样它与ent的意义就更接近：越大越好。
如果说信息增益和基尼指数等价的话，那么对于每一个划分，两者对于它的评价应该是一致的。这并不意味着它们的数值相等，而是指它们的偏序关系是一致的：如果信息增益认为划分A比划分B好，那么基尼指数也能推出划分A比划分B好。简而言之，它们对一组划分的排序应该是完全一致的。
所以我们想找的反例就是信息增益认为划分A比划分B好，但基尼指数却得到相反的结论。
从图中我们可看到，大体上两种标准的趋势是一样的。似乎只要将它们进行y轴上的放缩，就能得到一个不错的拟合。但实际上，如红色箭头标注的那样，两种标准不是完全一致的。信息增益的同时，基尼指数却没有明显提升。可见，它们不是等价的。
但是它们对于最高点，也就是最优划分的判断是一致的。这又引起人的思考，是不是它们只是在局部有细微差别，但是对最优划分却总是一致呢？

进一步寻找反例

经过不断地试探，我找到了一组合适的反例：

属性值	4.4	5.0	5.1	5.1	6.0	6.0	6.1	6.1	6.1	6.3	6.3	6.4	6.5	6.8	6.8	7.7
类别	0	1	0	0	2	1	1	1	2	2	2	2	2	2	2	2

记原始数据集 $D D\,$ 的信息熵为 $E_{0}$
现在考虑两个划分：
$Dv_{1}$ ：属性值 $≤5.55\le 5.55$ 和 $>5.55\gt 5.55$ ，相应的信息增益记为 $E_{1}$ ，基尼指数为 $G_{1}$
$Dv_{2}$ ：属性值 $≤6.2\le 6.2$ 和 $>6.2\gt 6.2$ ，相应的信息增益记为 $E_{2}$ ，基尼指数为 $G_{2}$
经过计算得到：
$E_{0}=1.41973671$
$E1=0.60845859,G1=0.375E_{1}=0.60845859, \quad G_{1}=0.375$
$E2=0.55883437,G2=0.36111111E_{2}=0.55883437, \quad G_{2}=0.36111111$
而且 $E_{1}$ 是所有划分中信息增益的最大值， $G_{2}$

最低0.47元/天解锁文章