数字信号处理①信号的合成、分解、相关性及傅里叶系数的计算

dwgan

已于 2023-04-17 16:24:03 修改

阅读量3.4w

点赞数 37

分类专栏：数字信号处理文章标签：信号合成信号分解相关性傅里叶系数

于 2019-04-19 02:05:57 首次发布

本文链接：https://blog.csdn.net/qq_39432978/article/details/89391212

版权

数字信号处理专栏收录该内容

3 篇文章

订阅专栏

文章目录

一、信号的合成和分解
- （一）傅里叶级数
- （二）将正弦波合成方波
二、信号的相关性及傅里叶系数的计算
三、信号的分解
- 从信号合成到信号分解
最后

一、信号的合成和分解

任何周期信号都可以由正弦信号合成，反之，任何周期信号都可以分解为正弦波的叠加，这是傅里叶变换告诉我们的。为了理解该原理，让我们先从傅里叶级数开始

（一）傅里叶级数

由公式

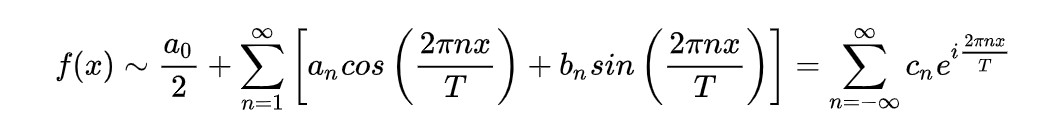
在这里插入图片描述

可以知道一个周期信号可以由正弦波叠加而成

（二）将正弦波合成方波

使用matlab生成基波及3、5、7、9、11次谐波

w=1000;%基波频率，单位Hz
f1=sin(2*pi*w*t);%基波信号
f3=sin(2*pi*3*w*t)/3;%3次谐波信号
f5=sin(2*pi*5*w*t)/5;%5次谐波信号
f7=sin(2*pi*7*w*t)/7;%7次谐波信号
f9=sin(2*pi*9*w*t)/9;%9次谐波信号
f11=sin(2*pi*11*w*t)/11;%11次谐波信号

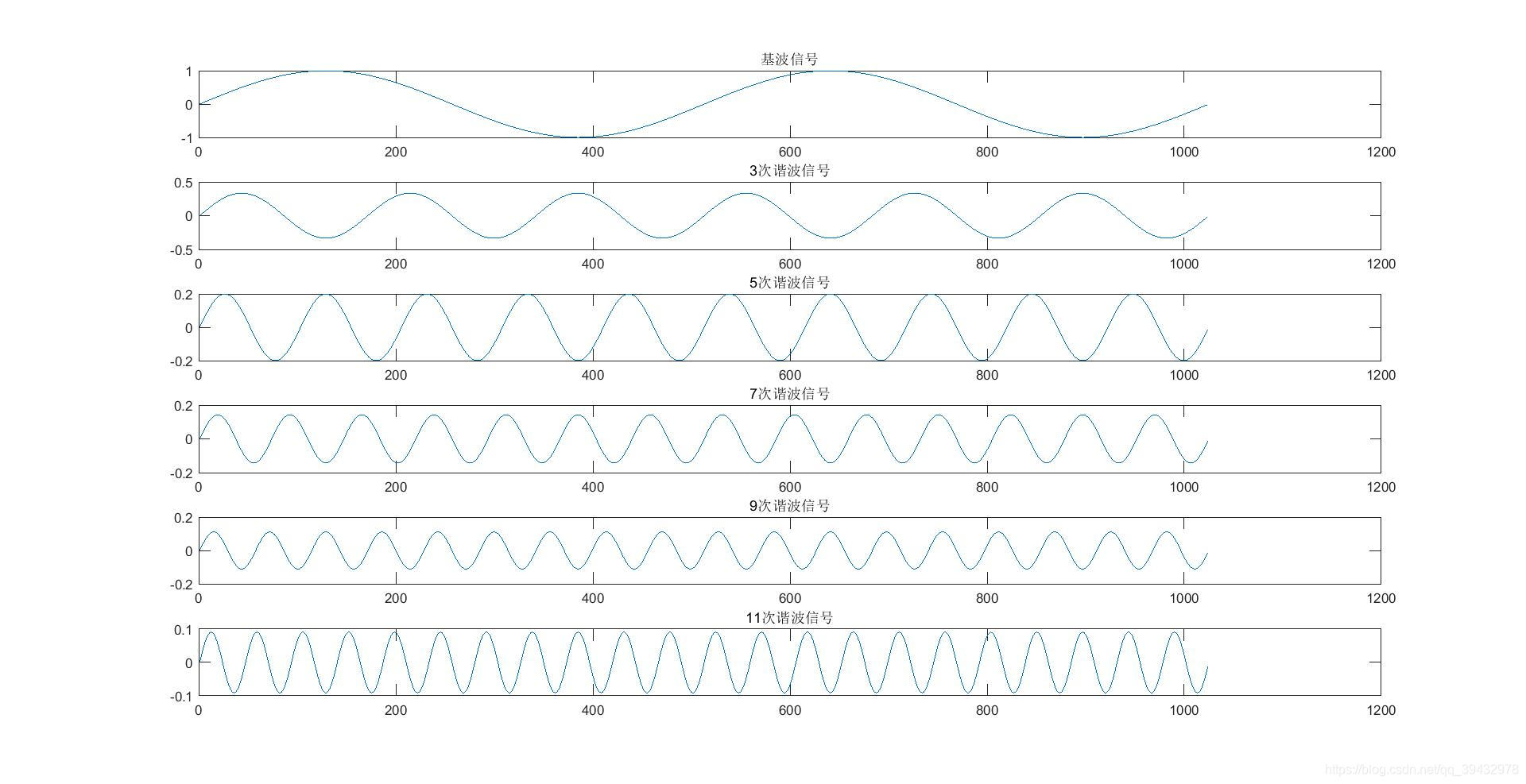
matlab生成及次谐波

将基波及3、5、7、9、11次谐波进行叠加

f=f1+f3+f5+f7+f9+f11;

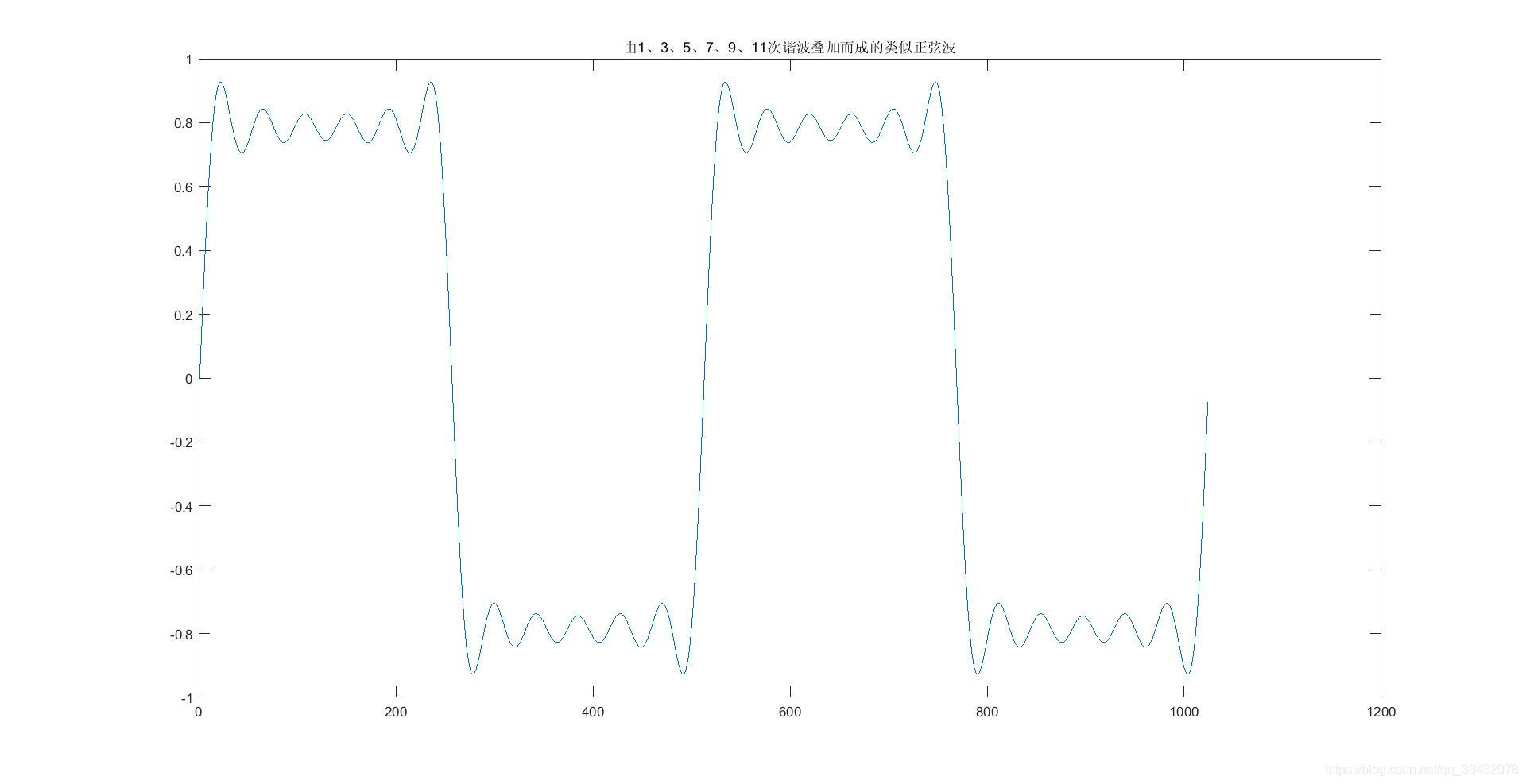
几次谐波叠加而成的方波

这里只是使用了基波及3、5、7、9、11次谐波来叠加，已经可以看得出方波的雏形了，如果使用更多的13、15、17、19次乃至更高次的谐波来叠加，则会更接近方波。事实上一个完整的方波是无限多、无限高次谐波的叠加。另外提一点，即使使用无限多、无限高次谐波来合成方波仍会发现会在间断点出现剑锋，大概是9%的偏差，这个现象叫做吉布斯现象，因为当谐波次数取得很大时，间断点尖峰下的面积趋近于零，从能量的角度看来，合成波形与原方波没有区别。
回到顶部

二、信号的相关性及傅里叶系数的计算

（一）信号的相关性

信号的相关性是信号处理领域中最重要的概念之一，无论是滤波、信号恢复、去噪以及压缩感知等技术，从本质上都离不开信号的相关性。
所谓信号的相关性，抽象上的理解就是两个信号之间的相关程度。数学上则可以表示为两个信号的内积，对于连续信号可以用两个信号相乘对于时间进行积分（注意和卷积的概念进行区分），对于离散信号则是向量内积求和
一个信号与固定频率信号相乘，如果该信号含有固定频率信号的频率成分，那么乘积的结果作积分不为零，反之为零。因为随机信号不含有固定的频率，所以一个随机信号与任意一个固定频率信号相乘做积分结果为零，这正是傅里叶变换能消除随机干扰的原因

（二）傅里叶系数

由傅里叶系数计算公式
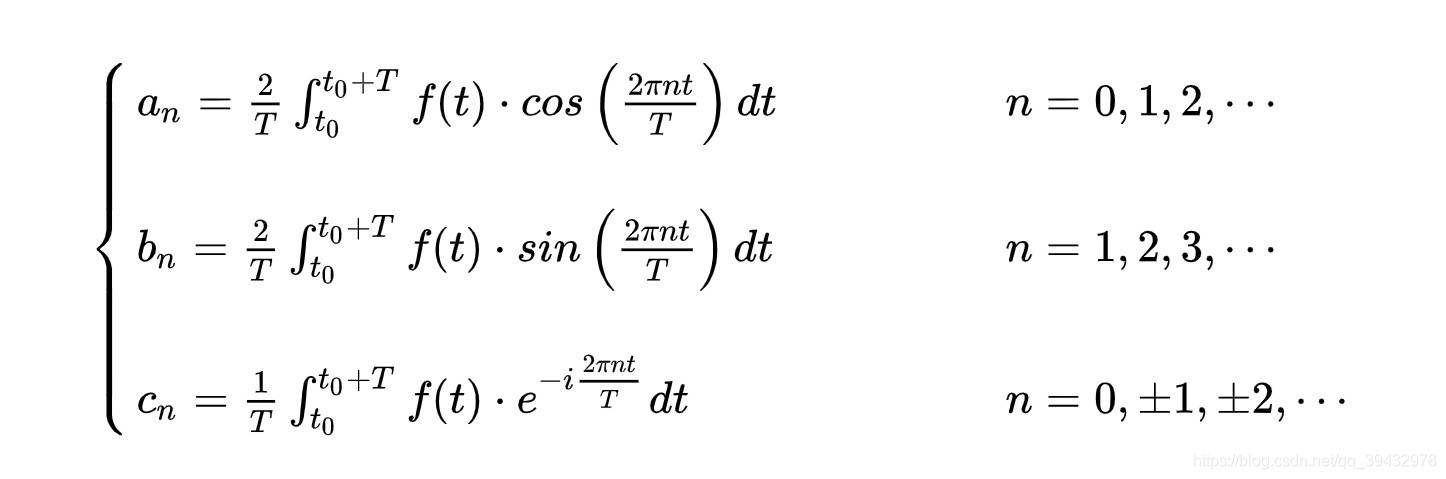
可知要计算傅里叶系数就是将原信号与一个固定频率的信号进行相乘然后求积分，我们知道任何一个信号都是由正弦波叠加而成的，我们只要将一个信号与一个已知频率的信号相乘求积分，就知道了在该信号中这个频率的分量，这个过程其实就是求傅里叶系数
回到顶部

（三）相关性的验证及幅值、相位的计算

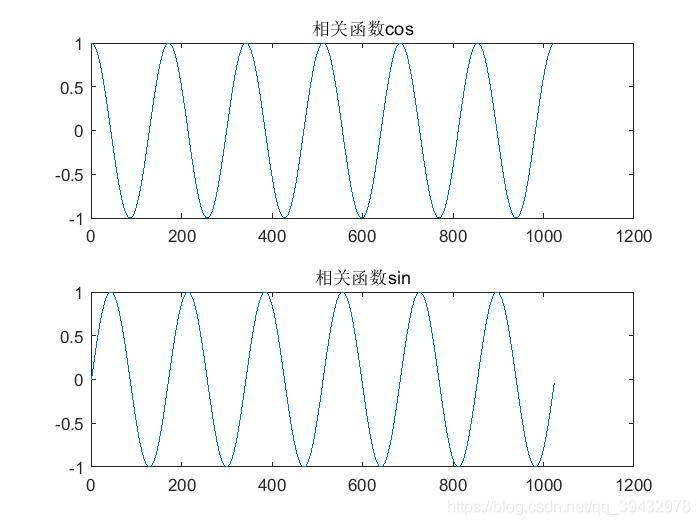
使用matlab生成相关函数，该相关函数的频率与合成信号的三次谐波频率相同

f_cos=cos(2*pi*3*w*t);%相关函数，用于与合成信号作相关
f_sin=sin(2*pi*3*w*t);%相关函数，用于与合成信号作相关

这里提一点，为什么要用两个信号（cos、sin）来乘呢？你可以把这个过程当做信号的分解，其实这两个信号（cos、sin）是两个正交信号，相当于把原信号分解到两个正交信号上
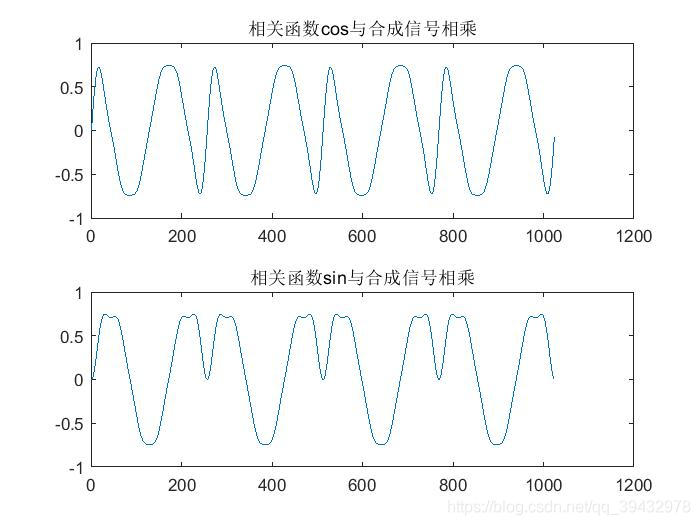
将相关信号与合成信号相乘

f_relaven_cos=f.*f_cos;%将合成信号与相关函数相乘，得到实部
f_relaven_sin=f.*f_sin;%将合成信号与相关函数相乘，得到虚部

在这里插入图片描述

将相乘后的信号求积分

sum_data_cos=sum_len(f_relaven_cos,N);%实部求和
sum_data_cos=sum_data_cos/N;
sum_data_sin=sum_len(f_relaven_sin,N);%虚部求和
sum_data_sin=sum_data_sin/N;

在这里插入图片描述

求幅值，我们的三次谐波中的幅值正好是一除以三再除以二也就是1.66666666666666…，得出结论原信号与该频率的信号相关，并且原信号中该频率成分分量的幅值为1.666666666666666，

sum_data=sqrt(sum_data_cos^2+sum_data_sin^2);

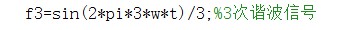
在这里插入图片描述

若要从能量的角度解释，就是原信号中该频率分量的成分所占能量为0.0278

sum_data_energy=sum_data_cos^2+sum_data_sin^2;

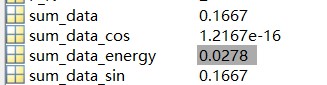
在这里插入图片描述

再来求一下相角

angle_data=atan(sum_data_sin/sum_data_cos)*180/pi;

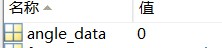
在这里插入图片描述

初始相位是零看不出结果，我们将三次谐波进行移相，再求相角，注意这时候可能合成的已经可能不是正弦波了

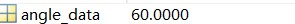
在这里插入图片描述

三、信号的分解

从信号合成到信号分解

前面的验证我们知道任何一个信号都可以由正弦波合成，那么反过来，任何信号都可以分解为正弦波的叠加。那么问题来了，怎样分解呢？答案就是傅里叶变换。但是傅里叶变换太复杂了，有没有更简单的理解方式呢？我们可以从傅里叶级数出发。
我们知道，欲求一个信号中某种频率的分量，只要将这个信号与欲求频率的信号相乘求积分就能得到这个信号中该频率的含量
再反过来，欲知一个信号中含有那些频率成分及各成分的分量，那就将这个信号与任意频率的信号相乘求积分（作相关），就能得到该信号中所含的所有频率成分及各个分量大小。
但是，与任意频率作相关，这个计算量也太大了吧。。。所以只需要对那奎斯特采样频率一半的信号作相关就够了，并且将任意频率抽取，即每隔多少频率求一次相关，这就是频谱分辨率，怎么越来越像傅里叶变换，没错这就是傅里叶变换。但是傅里叶变换是连续的，在数字系统中无法使用，所以要用离散傅里叶变换，但是离散傅里叶变换计算量还是很大，于是根据离散傅里叶变换的奇、偶、虚、实特特性，快速傅里叶变换诞生了，并且加速了数字信号处理的发展。