【机器学习】集成学习 (Ensemble Learning) (三) —— Boosting 与 Adaboost + GBDT

本文链接：https://blog.csdn.net/qq_39478403/article/details/112774505

本文深入解析集成学习中的提升法(Boosting)，详细介绍了Adaboost与梯度提升(Gradient Boosting)的原理、应用场景及Python实现。通过示例代码帮助读者理解算法细节。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

【机器学习】集成学习 (Ensemble Learning) (二) —— Bagging 与 Random Forest

【机器学习】集成学习 (Ensemble Learning) (四) —— Stacking 与 Blending

2.2 提升法 (Boosting)

2.2.1 自适应提升 (Adaboost)

2.2.2 梯度提升 (Gradient Boosting)

2.2 提升法 (Boosting)

在顺序化的方法中，组合起来的不同弱模型之间不再相互独立地拟合。其思想是迭代地拟合模型，使模型在给定步骤上的训练依赖于之前的步骤上拟合的模型。提升法 (Boosting) 是这些方法中最著名的一种，它生成的集成模型通常比组成该模型的弱学习器偏差更小。

Boosting 的工作思路 和 Bagging 类似：构建一系列弱学习器模型，将它们聚合起来得到一个性能更好的强学习器。然而，与重点在于 减小方差的 Bagging 不同，Boosting 着眼于以一种适应性很强的方式顺序拟合多个弱学习器。序列中每个模型在拟合的过程中，会 更加重视先前模型处理得很糟糕的观测数据。

更直观地，每个弱学习器模型都把注意力集中在目前最难拟合的观测数据上，直至最后获得一个具有较低偏差的强学习器（注意，Boosting 也有减小方差的效果）。和 Bagging 一样，Boosting 也可以用于 回归和分类 问题。由于其重点在于减小偏差，用于 Boosting 的基础模型通常是那些 低方差高偏差的模型。例如，如果想要使用树作为基础模型，我们将主要选择只有少许几层的较浅决策树。而选择低方差高偏置模型作为 Boosting 弱学习器的另一个重要原因是：这些模型拟合的计算开销较低（参数化时自由度较低）。实际上，由于拟合不同模型的计算无法并行处理（与Bagging 不同），顺序地拟合若干复杂模型会导致计算开销变得非常高。

一旦选定了弱学习器，我们还需定义它们的拟合方式和聚合方式。

常见的两个重要的 Boosting 算法是：自适应提升 (Adaboost) 和 梯度提升 (Gradient Boosting)。这两种元算法在顺序化过程中创建和聚合弱学习器的方式存在差异。Adaboost 算法会 更新附加给每个训练数据集中观测数据的权重，而 Gradient Boosting 算法则会 更新这些观测数据的值。产生差异的主要原因是：两种算法解决优化问题（寻找最佳模型 —— 弱学习器的加权和）的方式不同。

2.2.1 自适应提升 (Adaboost)

定义

事实上，对于 二分类 问题，可将 Adaboost 算法表述为以下过程：首先，使用一个弱学习器在原始数据集上训练；其次，根据误分类的概率相应地更新原始数据集中观测数据的权重，并用得到的新数据集训练一个新的弱学习器，而该学习器将 重点关注当前集成模型误分类的观测数据；然后，根据一个 表示该弱模型性能的更新系数 (区别于上述更新数据集观测数据的权重)，将弱学习器添加到集成模型的加权和中 —— 弱学习器的性能越好，它对集成模型/强学习器的贡献越大。

特别地，假设存在一个数据集，其中有 N 项观测数据，希望在给定的一组弱学习器模型下使用 Adaboost 算法。起始阶段（序列中的第一个模型），所有的观测数据都具有均等初始权重 1/N。然后，将以下步骤重复 L 次（作用于序列中的 L 个学习器）：

使用当前观测数据的权重拟合可能的最佳弱学习器模型；
计算更新系数的值，更新系数是弱学习器的某种标量化评估指标，它表示相对集成模型来说，该弱学习器的分量如何；
通过添加新的弱学习器与其更新系数的乘积来更新强学习器计算新观测数据的权重，该权重表示希望在下一轮迭代中对观测数据的关注倾向（预测错误的观测数据增加权重，而正确分类的观测数据权重减小）。

重复这些步骤，可以顺序地构建出 L 个模型，并根据各学习器性能系数对它们进行加权线性组合。更具体地：

步骤

注意，上述过程中的 α 不仅 用于更新样本权重，还 作为该弱分类器的（分类结果）的权重系数，用于最后模型集成时的加权求和。

算法

此外，Adaboost 算法有一些变体，比如 LogitBoost（分类）或 L2Boost（回归），它们的差异主要取决于损失函数的选择。

举例

同时，用 Python 实现 Adaboost 算法：

实现

1. 导入必要的依赖

import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.ensemble import AdaBoostClassifier

2. 实现决策树桩（单层决策树）

class DecisionTreeClassifierWithWeight:
    ''' 决策树桩 (Decision Tree Stump) - 基于单个特征决策 '''
    def __init__(self):
        # 初始化参数组合
        self.best_err = 1     # 最小加权错误率 
        self.best_fea_id = 0  # 最优特征 id
        self.best_thres = 0   # 选定特征的最优阈值
        self.best_op = 1      # 最优阈值符号，其中 op=1: >, op=0: < 

    def fit(self, X, y, sample_weight=None):
        if sample_weight is None:
            sample_weight = np.ones(len(X)) / len(X)  # 初始权重均等
            
        n = X.shape[1]  # 特征变量数
        # 遍历各项特征
        for i in range(n):
            feature = X[:, i]  # 选定第 i 个特征列
            fea_unique = np.sort(np.unique(feature))  # 将所有特征值从小到大排序
            # 遍历第 i 个特征下的各样本
            for j in range(len(fea_unique)-1):
                # 枚举阈值
                thres = (fea_unique[j] + fea_unique[j+1]) / 2  # 逐一设定可能阈值 (取在两两样本之间)
                # 枚举二分类正负例判断 (lesser than / greater than)
                for op in (0, 1):
                    # 预测
                    y_ = 2*(feature >= thres)-1 if op==1 else 2*(feature < thres)-1  # 判断何种符号下弱分类器为最优 (+1 或 -1) / 误差最小
                    # 计算误差
                    err = np.sum((y_ != y) * sample_weight)
                    # 若当前参数组合可获得更低错误率，则更新最优参数
                    if err < self.best_err:  
                        self.best_err = err
                        self.best_fea_id = i
                        self.best_thres = thres
                        self.best_op = op
        return self
       
    def predict(self, X):
        feature = X[:, self.best_fea_id]
        return 2*(feature >= self.best_thres)-1 if self.best_op==1 else 2*(feature < self.best_thres)-1

    def score(self, X, y, sample_weight=None):
        y_pred = self.predict(X)  # 预测标签
        if sample_weight is not None:
            return np.sum((y_pred == y) * sample_weight) 
        return np.mean(y_pred == y)

3. 决策树桩测试

# 决策树桩测试
X, y = load_breast_cancer(return_X_y=True)  # 加载数据集
y = 2*y - 1  # 将 labels 的 0 / 1 取值映射为 -1 / 1 取值 
X_train, X_test, y_train, y_test = train_test_split(X, y)  # 默认 test_size=0.3
DecisionTreeClassifierWithWeight().fit(X_train, y_train).score(X_test, y_test)  # 得分：0.9090909090909091

4. 以决策树桩作为基本弱学习器，构造 Adaboost

class AdaBoostClassifier_:
    ''' 以决策树桩作为弱分类器构造 Adaboost '''
    def __init__(self, n_estimators=50):
        self.n_estimators = n_estimators  # 弱学习器(决策树桩)数
        self.estimators = []
        self.alphas = []  # 权重列表

    def fit(self, X, y):
        sample_weight = np.ones(len(X)) / len(X)  # 初始化样本权重均为 1/N
        # 依次串行训练各弱学习器
        for _ in range(self.n_estimators):
            dtc = DecisionTreeClassifierWithWeight().fit(X, y, sample_weight)  # 拟合当前弱学习器
            alpha = 1/2 * np.log((1 - dtc.best_err) / dtc.best_err)  # 计算当前弱学习器 权重系数α
            y_pred = dtc.predict(X)  # 当前弱学习器预测结果 (+1 或 -1)
            sample_weight *= np.exp(-alpha * y_pred * y)  # 根据公式 更新迭代样本权重 （y_pred * y 分类正确为 1 错误为 -1）
            sample_weight /= np.sum(sample_weight)  # 根据公式 用总样本权重归一化
            self.estimators.append(dtc)  # 记录当前弱学习器
            self.alphas.append(alpha)    # 记录当前弱学习器 权重系数α
        return self   
   
    def predict(self, X):
        y_pred = np.empty((len(X), self.n_estimators))  # 预测结果二维数组，其中每列代表一个弱学习器的预测结果
        # 依次遍历各弱学习器进行推理
        for i in range(self.n_estimators):
            y_pred[:, i] = self.estimators[i].predict(X)
        y_pred = y_pred * np.array(self.alphas)  # 将各预测结果与相应的训练权重之积作为集成预测结果
        return 2 * (np.sum(y_pred, axis=1) > 0) - 1  # 以 0 为阈值，判断并映射为 -1 和 1

    def score(self, X, y):
        y_pred = self.predict(X)
        return np.mean(y_pred==y)

5. 官方和自定义 Adaboost 测试对比

# 官方 Adaboost 测试
AdaBoostClassifier().fit(X_train, y_train).score(X_test, y_test)   # 0.965034965034965

# 自定义 Adaboost 测试
AdaBoostClassifier_().fit(X_train, y_train).score(X_test, y_test)  # 0.965034965034965

可见于官方实现结果并无差异！

此外，Adaboost 还存在另一种解释：

其他

2.2.2 梯度提升 (Gradient Boosting)

与 Adaboost 算法类似，梯度提升 (GB) 集成学习算法也是基于多个弱学习器的训练效果的加权进行最终判决的，且每轮训练也基于前一轮训练效果进行针对性地更新迭代。但与Adaboost 聚焦于 前一轮训练错误 的样本机制不同，GB 聚焦于 前一轮训练的残差。比如 A 的真实年龄是 18 岁，但第一棵树的预测年龄是 12 岁，差了 6 岁，即残差为 6 岁。那么在第二棵树里我们把 A 的年龄设为 6 岁去学习，如果第二棵树真的能把 A 分到 6 岁的叶子节点，那累加两棵树的结论就是A 的真实年龄；如果第二棵树的结论是5岁，则 A 仍然存在 1 岁的残差，第三棵树里 A 的年龄就变成 1 岁，继续学习。

GB 每次迭代中拟合残差来学习一个弱学习器，而残差的方向即为我们全局最优的方向。当损失函数是 平方损失 时，GB 将 平方损失函数的负梯度 在当前模型的值作为下个模型训练的目标函数。沿着平方损失函数负梯度方向迭代 (GB 的核心)，使得损失函数、模型偏差越来越小。对弱分类器的要求一般是 足够简单，并且是 低方差和高偏差 的。因为训练过程是通过降低偏差来不断提高最终分类器精度的、

将决策树 CART 放入 GB 模型框架中，就得到了一个集成模型 —— GBDT 模型。

GBDT (Gradient Boosting Decision Tree) 又叫 MART（Multiple Additive Regression Tree)，作为一种迭代的决策树算法，由多棵决策树组成，在被提出之初就和 SVM 一起被认为是泛化能力较强的算法。注意，GBDT 中的树是回归树（不是分类树），GBDT 用于回归预测，调整后也可以用于分类。业界中，Facebook 使用其来自动发现有效的特征、特征组合，来作为 LR 模型中的特征，以提高 CTR 预估（Click-Through Rate Prediction）的准确性；GBDT 在淘宝的搜索及预测业务上也发挥了重要作用。

(1) 分类与回归树 (CART)

决策树模型分为分类树和回归树，分类树 常用于分类问题，如用户性别、网页是否是垃圾页面、用户是不是作弊等；回归树 常用于回归问题，如预测用户年龄、点击率、网页相关程度等。

回归树 总体流程类似于分类树，但区别在于，其每个节点都会得到一个预测值。以年龄为例，该预测值等于所有属于该节点的人的年龄平均值。分枝时，穷举每个特征的每个阈值寻找最优切分变量和最优切分点，但衡量的准则 不再是分类树中的基尼系数，而是 平方误差最小化。即预测错误的人数越多，平方误差越大，通过最小化平方误差找到最可靠的分枝依据。分枝直到每个叶子节点上人的年龄都唯一或者达到预设的终止条件(如叶子个数上限)，若最终叶子节点上人的年龄不唯一，则以该节点上所有人的平均年龄做为该叶子节点的预测年龄。

(2) 提升树 (Boosting Tree)

提升树 (Boosting Tree) 算法

提升树 (Boosting Tree) 例子

提升树 (Boosting Tree) 实现

from collections import defaultdict
import numpy as np


class BoostingTree:
    def __init__(self, error=1e-2):
        self.error = error                     # 最大容忍误差值 / 最小需求精度
        self.candidate_splits = []             # 候选切分点列表
        self.split_index = defaultdict(tuple)  # 由于要多次切分数据集，故预先存储，切分后数据点的索引
        self.split_list = []                   # 最终各个基本回归树的切分点
        self.c1_list = []                      # 切分点左区域取值（均值）
        self.c2_list = []                      # 切分点右区域取值（均值）
        self.N = None                          # 数组元素个数
        self.n_split = None                    # 切分点个数

    # 切分数组函数
    def split_arr(self, X_data):
        self.N = X_data.shape[0]
        # 候选切分点
        for i in range(1, self.N):
            self.candidate_splits.append((X_data[i][0] + X_data[i-1][0]) / 2)  # 相邻两数的中间值
        self.n_split = len(self.candidate_splits)  # 切分点个数
        # 切成两部分 - 二叉决策树分裂
        for split in self.candidate_splits:
            left_index = np.where(X_data[:, 0] <= split)[0]      # 左子树切分点索引
            right_index = np.where(X_data[:, 0] > split)[0]      # 右子树切分点索引
            self.split_index[split] = (left_index, right_index)  # 记录切分点索引
        return

    # 计算各切分点的误差
    def calculate_error(self, split, y_result):
        indexs = self.split_index[split]
        left = y_result[indexs[0]]   # 左子树切分点
        right = y_result[indexs[1]]  # 右子树切分点
        # 可证明：损失函数为平方损失 (MSE) 时，叶节点的最佳预测为叶节点残差的均值
        c1 = np.sum(left) / len(left)    # 左子树切分点均值
        c2 = np.sum(right) / len(right)  # 右子树切分点均值
        y_result_left = left - c1        # 左子树残差
        y_result_right = right - c2      # 右子树残差
        result = np.hstack([y_result_left, y_result_right])   # 拼接左右子树残差
        result_square = np.apply_along_axis(lambda x: x ** 2, 0, result).sum()  # 残差平方损失 (MSE)
        return result_square, c1, c2

    # 获取最佳切分点，并返回对应的残差
    def best_split(self,y_result):
        # 默认第一个为最佳切分点
        best_split = self.candidate_splits[0]
        min_result_square, best_c1, best_c2 = self.calculate_error(best_split, y_result)
        # 逐点计算、比较和更新
        for i in range(1, self.n_split):
            result_square, c1, c2 = self.calculate_error(self.candidate_splits[i], y_result)  
            # 更新最佳切分点 索引、误差、左右子树切分点均值
            if result_square < min_result_square:
                best_split = self.candidate_splits[i]
                min_result_square = result_square
                best_c1 = c1
                best_c2 = c2
        # 记录本次最佳（误差最小）切分点信息
        self.split_list.append(best_split)
        self.c1_list.append(best_c1)
        self.c2_list.append(best_c2)
        return

    # 基于当前组合树，预测任意输入数据 X 的输出值
    def predict_x(self, X):
        s = 0
        for split, c1, c2 in zip(self.split_list, self.c1_list, self.c2_list):
            if X < split:
                s += c1  # 累加
            else:
                s += c2  # 累加
        return s

    # 每添加一颗回归树，就要更新 y, 即基于当前组合回归树的预测残差
    def update_y(self, X_data, y_data):
        y_result = []
        for X, y in zip(X_data, y_data):
            y_result.append(y - self.predict_x(X[0]))  # 残差
        y_result = np.array(y_result)
        print(f'residual: {np.round(y_result, 2)}')  # 输出每次拟合训练数据的残差
        res_square = np.apply_along_axis(lambda x: x ** 2, 0, y_result).sum()
        return y_result, res_square
    
    # 拟合/训练
    def fit(self, X_data, y_data):
        self.split_arr(X_data)  # 切分输入数据
        y_result = y_data  # 获取输入数据标签
        while True:
            self.best_split(y_result)
            y_result, result_square = self.update_y(X_data, y_data)
            # 达到精度即停止, 否则继续天添加回归树学习
            if result_square < self.error:
                print(f"training error: {result_square}")
                break
        return
    
    # 预测/推理
    def predict(self, X):
        return self.predict_x(X)


if __name__ == '__main__':
    # 自定义训练集
    data = np.array([[1, 5.56], [2, 5.70], [3, 5.91], [4, 6.40], [5, 6.80],
                     [6, 7.05], [7, 8.90], [8, 8.70], [9, 9.00], [10, 9.05]])
    X_data = data[:, :-1]          # 样本
    y_data = data[:, -1]           # 标签
    bt = BoostingTree(error=0.18)  # 实例化 GBDT 对象，最大容忍误差/最小需求精度设为 0.18
    bt.fit(X_data, y_data)         # 拟合/训练
    
    print(f'切分点：{bt.split_list}')
    print(f'切分点左区域取值: {np.round(bt.c1_list ,2)}')
    print(f'切分点右区域取值: {np.round(bt.c2_list, 2)}')
    print(f'任意点预测测试：2.3 - {bt.predict(np.array([2.3]))},  2.8 - {bt.predict(np.array([2.8]))}, 3.6 - {bt.predict(np.array([3.6]))}')

residual: [-0.68 -0.54 -0.33  0.16  0.56  0.81 -0.01 -0.21  0.09  0.14]
residual: [-0.16 -0.02  0.19 -0.06  0.34  0.59 -0.23 -0.43 -0.13 -0.08]
residual: [-0.31 -0.17  0.04 -0.2   0.2   0.45 -0.01 -0.21  0.09  0.14]
residual: [-0.15 -0.01  0.2  -0.04  0.09  0.34 -0.12 -0.32 -0.02  0.03]
residual: [-0.22 -0.08  0.13 -0.11  0.02  0.27 -0.01 -0.21  0.09  0.14]
residual: [-0.07  0.07  0.09 -0.15 -0.02  0.23 -0.05 -0.25  0.05  0.1 ]
training error: 0.17217806498628246
切分点：[6.5, 3.5, 6.5, 4.5, 6.5, 2.5]
切分点左区域取值: [ 6.24 -0.51  0.15 -0.16  0.07 -0.15]
切分点右区域取值: [ 8.91  0.22 -0.22  0.11 -0.11  0.04]
任意点预测测试：2.3 - 5.63,  2.8 - 5.818310185185186, 3.6 - 6.551643518518518

(3) GBDT

GBDT 回归树算法

GBDT 正则化

GBDT 损失函数

在 sklearn 中，梯度提升回归树 的损失函数有四种：

ls：平方损失 (最小二乘损失、MSE)
lad：绝对损失 (MAE)
huber：huber 损失
quantile：分位数损失

而 梯度提升分类树 的损失函数有两种：

exponential：指数损失 (用指数损失函数时，GBDT 退化为 Adaboost)
deviance：对数损失

可证明的结论

损失函数为 平方损失 (MSE) 时，叶节点的最佳预测为叶节点 残差的均值
损失函数为 绝对损失 (MAE) 时，叶节点的最佳预测为叶节点 残差的中位数

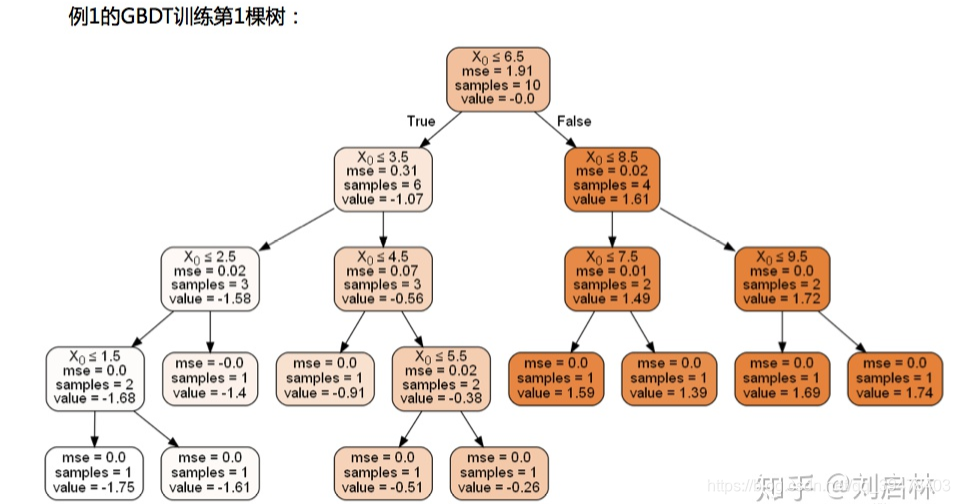
GBDT 例子

GBDT 优点

可以灵活处理各种类型的数据，包括连续值和离散值。
易于特征组合和特征选择。
在相对少的调参时间情况下，预测的准确率也可以比较高。这是相对 SVM 来说的。
使用一些健壮的损失函数，对异常值的鲁棒性非常强。比如 Huber 损失函数和 Quantile 损失函数。

GBDT 缺点

由于弱学习器之间存在依赖关系，难以并行训练数据。不过可以通过自采样的 SGBT 来达到部分并行。
数据维度高，计算复杂度高

GBDT 应用

GBDT 使用

# GBDT 分类器例程 https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingClassifier.html#sklearn.ensemble.GradientBoostingClassifier
from sklearn.datasets import make_hastie_10_2
from sklearn.ensemble import GradientBoostingClassifier

X, y = make_hastie_10_2(random_state=0)
X_train, X_test = X[:2000], X[2000:]
y_train, y_test = y[:2000], y[2000:]

clf = GradientBoostingClassifier(n_estimators=400, learning_rate=1.0, max_depth=1, random_state=0).fit(X_train, y_train)    
clf.score(X_test, y_test)  # 0.9434

# GBDT 回归器例程 https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingRegressor.html#sklearn.ensemble.GradientBoostingRegressor
from sklearn.datasets import make_regression
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.model_selection import train_test_split

X, y = make_regression(random_state=0)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

reg = GradientBoostingRegressor(n_estimators=300, random_state=0)
reg.fit(X_train, y_train)

print(f"predict X_test[1:2]: {reg.predict(X_test[1:2])}")  # [-60.9311096]
reg.score(X_test, y_test)  # 0.43974018604625276

GBDT vs RF