递归算法
直接或间接的调用自身的算法称为递归函数,采用栈结构,先调用的最后返回。
主要形式就是先纵后横,一个分支走到底,再退回一个到兄弟节点,依次回退。
列出递归的三种形式:切蛋糕、递推公式、等价转换。
递归要素:
- 明确递归得到结果是什么
- 提取重复的逻辑,缩小问题的规模不断递去(大部分问题由大向小递归)
- 变化的参数
- 明确递归的终止条件
阶乘函数:
- 明问题:jiecheng(n) 返回n!
- 找重复:n!=n*(n-1)!=n*(n-1)*(n-2)!=.....
- 找变化:变化的量为参数
- 找边界:边界时n=0时,返回1
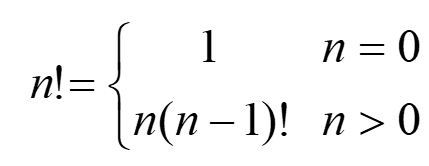
public int jiecheng(int n){
if (n == 1){
return 1;//递归出口
}
else return n * jiecheng(n-1);
//递归方程,从大到小
}字符串的翻转
- 明问题:recerse(s) 返回s的翻转字符
- 找重复:字符串的翻转等于最后一个字符+前n-1个字符的翻转....
- 找变化:变化的量为字符串的长度,作为参数
- 找边界:边界时长度为0时结束。
public static String reverse(String s,int n){
if (n==0) return "";
return s.charAt(n-1)+reverse(s,n-1);
}斐波那契数列(Fibonacci数列)
- 明问题:Fibonacci(n) 返回n对应的斐波那契数
- 找重复:n的斐波等于n-1的斐波+n-2的斐波
- 找变化:变化的量为参数
- 找边界:边界时n=1 || 2时,返回1
无穷数列1,1,2,3,5,8,13,21,34,55,……,称为Fibonacci数列。
斐波那契数列的分段函数(递归函数)为:
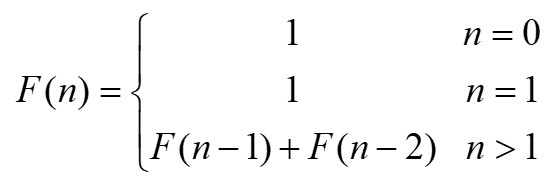
public int fibonacci(int n){
if (n == 1 || n == 2){
return 1;//递归结束位置
}
else return fibonacci(n-1) + fibonacci(n-2);
//递归函数
}最大公约数

- 明问题:辗转相除的m%n
- 找重复:m与n的最大公约数由n与m%n的最大公约数决定...依次类推
- 找变化:变化的量为m,n的取值。
- 找边界:边界时m%n==0时,返回n
public static int gcb(int m,int n){
if (m%n==0) return n;
return gcb(n,m%n);
}指数运算的改进
求:
基本思想改变底数与指数,将底数变为原来的平方,则相应的指数变为原来的二倍。

private static int pow0(int a,int n) {
if (n==0) return 1;
int res=a;//底数
int ex=1;//指数
while(ex*ex<n){//ex*ex来判断下一层的res*res是否超过a的n次幂
res=res*res;//改变底数
ex*=2;//改变指数
}
return res*pow0(a,n-ex);//递归思想,递归剩余部分,不是2的倍数
}上楼梯问题
一共有n层楼梯,每次只能上1层或2层或3层,问一共有几种上楼的方法。
- 明问题:walker(n) 返回n层楼梯的走法
- 找重复:若第一次上1层,则变成求剩余n-1层有几种走法问题;若第一次上2层,则变成求剩余n-2层有几种走法问题;若第一次上3层,则变成求剩余n-3层有几种走法问题;
- 找变化:楼梯的层数在发生变化
- 找边界:当楼梯只有1层或2层或3层时分别有1种,2种,4种走法
private static int walker(int n) {//此函数返回上n层楼梯所需的时间
if (n==0) return 0;
if (n==1) return 1;
if (n==2) return 2;
if (n==3) return 4;
return walker(n-1)+walker(n-2)+walker(n-3);
}递归排序
- 明问题:sort(nums,n)返回0~n排好序的数组
- 找重复:对n个元素排序可以看作最后一个元素插入对前n-1个元素的排序
- 找变化:变化的量为排序的边界值的取值。
- 找边界:边界时n==0时结束
public static void sort(int []nums,int n){//n表示最后一个元素的索引
if (n==0) return;
sort(nums,n-1);
int t=nums[n];
int i=n-1;
for (;i>=0;i--){
if (nums[i]<=t) break;
nums[i+1]=nums[i];//数组的插入操作
}
nums[i+1]=t;//最终空下来的位置时i+1
}瓷砖铺放问题
有⼀长度为N(1<=N<=10)的地板,给定两种不同瓷砖:⼀种长度为1,另⼀种长度为2,数⽬不限。要将这个长度为N的地板铺满,⼀共有多少种不同的铺法?
一共有n块砖,第一次铺两块就还剩f(N-2),第一次铺一块就还剩f(n-1)

public int cizhuan(int n){
if (n == 1){
return 1;
}
if (n == 2){
return 2;
}
return cizhuan(n-1) + cizhuan(n - 2);
}整数划分问题
将正整数n表示成一系列正整数之和:n=n1+n2+…+nk,其中n1≥n2≥…≥nk≥1,k≥1。正整数n的这种表示称为正整数n的划分。求正整数n的不同划分个数。


public int huafen(int n,int m){
if(n<1||m<1) return 0;
if (m == 1 || n == 1) return 1;
if (n == m || n < m) return huafen(n,n-1)+1;
return huafen(n,m-1)+huafen(n - m,m);
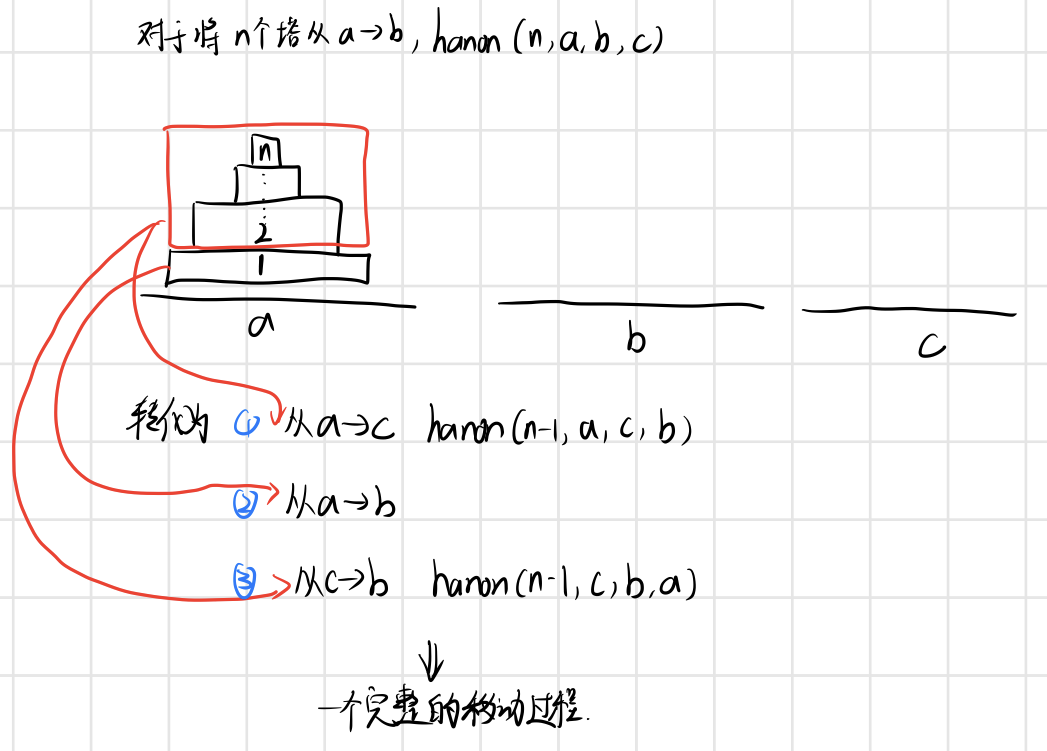
}Hanoi塔问题
设a,b,c是3个塔座。开始时,在塔座a上有一叠共n个圆盘,这些圆盘自下而上,由大到小地叠在一起。各圆盘从小到大编号为1,2,…,n,现要求将塔座a上的这一叠圆盘移到塔座b上,并仍按同样顺序叠置。在移动圆盘时应遵守以下移动规则:
规则1:每次只能移动1个圆盘;
规则2:任何时刻都不允许将较大的圆盘压在较小的圆盘之上;
规则3:在满足移动规则1和2的前提下,可将圆盘移至a,b,c中任一塔座上。
- 明问题:hannon(int n,char a,char b,char c){//起始盘,结束盘,辅助盘 将n个塔利用辅助盘c从a移动到b的解决措施。
- 找重复:对n个塔(a->b)的移动,转为将前n~2(一个整体)个从a->c(转化为将n-1个塔从a->c的问题),第1个从a->b,再将前n~2(一个整体)个从c->b的过程(转化为将n-1个塔从c->b的问题)
- 找变化:变化的量为移动塔的数量、起始盘、终止盘、辅助盘的取值。
- 找边界:边界时n==0时结束
public static void hannon(int n,char a,char b,char c){//起始盘,结束盘,辅助盘
if (n==0) return;
hannon(n-1,a,c,b);
System.out.println(a+"->"+b);
hannon(n-1,c,b,a);
}杨辉三角问题
每行端点与结尾的数为1.
每个数等于它上方两数之和。

public int Ytriangle(int i,int j){//获取每个坐标的值
if (i == j || j == 1) return 1;
return Ytriangle(i-1,j-1) + Ytriangle(i - 1,j);
}全排列问题:
给出n个数,打印出这n个数的全排列形式
每一个数都能放在第一个,交换函数实现
一直缩小序列,直至序列数只有一个,perm实现
特别注意为保证每一个都能放在第一个(1xxx的序列完全交换后,需要利用交换函数还原成1xxx,便于进行2xxx)

public static void swap(int[]list,int i,int j){
int t = list[i];
list[i] = list[j];
list[j] = t;
}
public static void perm(int[] list,int p,int r){
/*
perm实现
1xxx -> 2xx 5xx 6xx 无限缩小
*/
if (p == r){//只剩一个元素,输出该序列
for (int i = 0;i <= r;i++){
System.out.print(list[i] + " ");
}
System.out.println();;
}
else {
for (int j = p;j <= r;j++){//依次遍历每一个数
swap(list,j,p);//每一个数都与第一个数交换位置
perm(list,p+1,r);//继续缩小序列
swap(list,p,j );//将上一步换的数还原,便于下一个数字的交换
}
}
}分治策略整体思想:
将一个规模为n的问题分解为k个规模较小的子问题,这些子问题相互独立且与原问题相同,递归地解决这些问题,然后将各子问题的解合并得到原问题的解

一个分治法将规模为n的问题分成k个规模为n/m的子问题去解。设分解阀值n0=1,且adhoc解规模为1的问题耗费1个单位时间。再设将原问题分解为k个子问题以及用merge将k个子问题的解合并为原问题的解需用f(n)个单位时间。用T(n)表示该分治法解规模为|P|=n的问题所需的计算时间,则有:
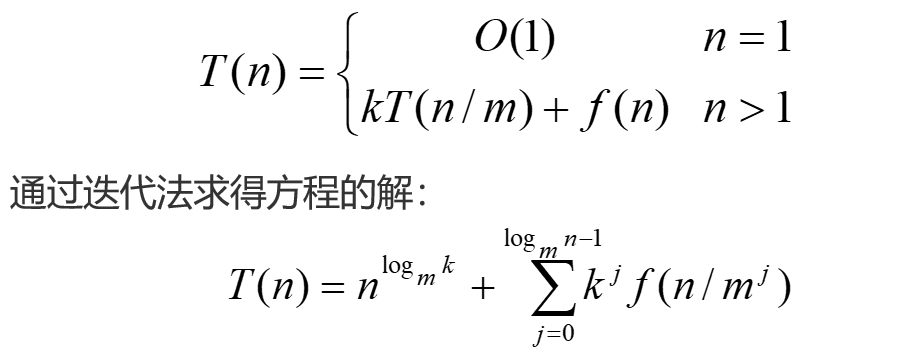
分治法的时间复杂度
- 将一个问题划分为同一类型的若干子问题,子问题的规模最好相同;
- 一般使用递归的方法来对这些子问题进行求解;
- 一般在解决这些子问题之后,算法将对这些子问题的解进行合并,并得到整个问题的最终解.
基于上述特征,我们可以得到分治算法的复杂度分析递推公式为、
二分搜索算法:
public static int binarySearch(int [] a, int x, int n)
{
// 在 a[0] <= a[1] <= ... <= a[n-1] 中搜索 x
// 找到x时返回其在数组中的位置,否则返回-1
int left = 0; int right = n - 1;
while (left <= right) {
int middle = (left + right)/2;
if (x == a[middle]) return middle;
if (x > a[middle]) left = middle + 1;
else right = middle - 1;
}
return -1; // 未找到x
}
大整数的乘法
X和Y均为n位的十进制整数,则X*Y需要进行次乘法运算。
将n位的十进制整数X与Y分为2段
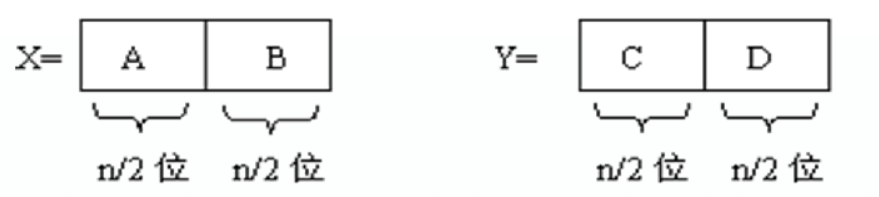
则
X = A * 10
+ B
Y = C * 10
+ D
XY = (A * 10
+ B) * (C * 10
+ D) = AC*
+ (AD + CB)*
+ BD
将原本的的计算量分治成了AC、AD、BC、BD四次乘法,故K = 4, m = 2,可得递归方程
要想改进算法的效率,必须减少乘法的次数
XY = (A * 10 + B) * (C * 10
+ D) = AC*
+ ((A - B)*(D - C) + AC + BD)*
+ BD
此时只需要计算AC、(A-B)*(D-C)、BD三个乘法,K = 3,M = 2,有较大改善
Strassen矩阵乘法
C = AB
矩阵乘法共计需要8次乘法
Strassen利用新的算法来计算2个2阶方阵的乘积
将矩阵的8次乘法转化为7次乘法
棋盘覆盖问题
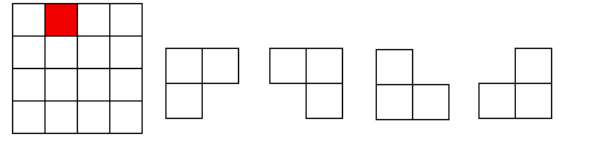
在一个×
个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为一特殊方格,且称该棋盘为一特殊棋盘。在棋盘覆盖问题中,要用图示的4种不同
形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。
易知,覆盖任意一个×
的特殊棋盘,用到的骨牌数恰好为(
-1)/3。
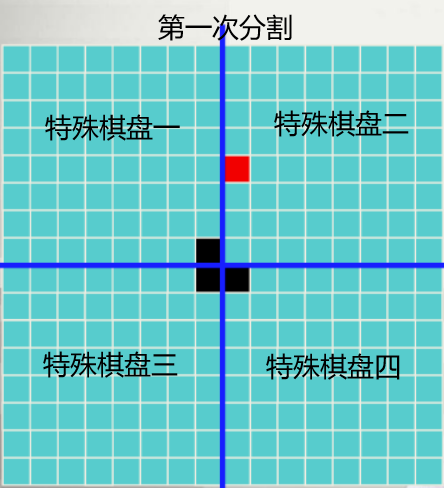
用分治策略,当k>0时,将
×
棋盘分割为4个
×
子棋盘,特殊方格比位于4个较小子棋盘之一,其余3个子棋盘中无特殊方格,且正好能被L型骨牌完全覆盖。
为了能将这三个无特殊方格的子棋盘转化为特殊棋盘,可以将L型骨牌覆盖这三个较小的棋盘的汇合处,则这三个子棋盘就转化成了四个较小规模的棋盘覆盖问题
递归地使用这种分割,直至棋盘简化为1×1棋盘,即每个棋盘都是特殊棋盘

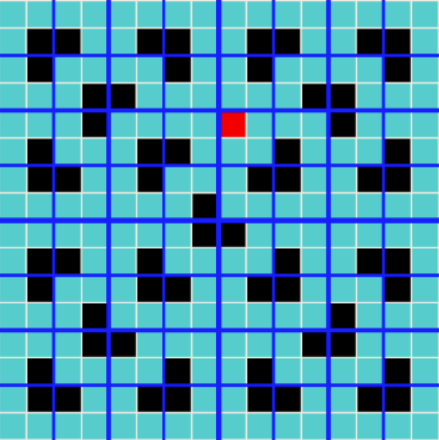

算法:
整型数组board表示棋盘。board[0][0]是棋盘的左上角方格。
tile是算法中的一个全局整型变量,用来表示L型骨牌的编号,其初始值为0
tr:每个棋盘左上角方格的行号
tc:每个棋盘左上角方格的列号
dr:特殊方格所在的行号
dc:特殊方格所在的列号
size:,棋盘规格为
×
public void chessBorad(int tr,int tc,int dr,int dc,int size){
if (size == 1) return;
int t = tile++;//L型骨牌号
int s = size/2;//分割后的棋盘大小
//左上角棋盘
if (dr < tr + s && dc < tc + s)//特殊方格在此棋盘中
chessBorad(tr,tc,dr,dc,s);//无限递归细分
else {//此棋盘中无特殊方格
borad[tr + s - 1][tc + s - 1] = t;//则用t号L型骨牌覆盖此棋盘的右下角(覆盖这三个较小的棋盘的汇合处)
chessBorad(tr,tc,tr + s - 1,tc + s - 1,s);//在对其进行特殊方格的棋盘覆盖
}
//右上角上角棋盘
if (dr < tr + s && dc >= tc + s)//特殊方格在此棋盘中
chessBorad(tr,tc + s,dr,dc,s);//无限递归细分
else {//此棋盘中无特殊方格
borad[tr + s - 1][tc + s] = t;//则用t号L型骨牌覆盖此棋盘的右下角(覆盖这三个较小的棋盘的汇合处)
chessBorad(tr,tc + s,tr + s - 1,tc + s,s);//在对其进行特殊方格的棋盘覆盖
}
//左下角棋盘
if (dr >= tr + s && dc < tc + s)//特殊方格在此棋盘中
chessBorad(tr + s,tc,dr,dc,s);//无限递归细分
else {//此棋盘中无特殊方格
borad[tr + s][tc + s - 1] = t;//则用t号L型骨牌覆盖此棋盘的右下角(覆盖这三个较小的棋盘的汇合处)
chessBorad(tr + s,tc,tr + s,tc + s - 1,s);//在对其进行特殊方格的棋盘覆盖
}
//右下角棋盘
if (dr >= tr + s && dc >= tc + s)//特殊方格在此棋盘中
chessBorad(tr + s,tc + s,dr,dc,s);//无限递归细分
else {//此棋盘中无特殊方格
borad[tr + s][tc + s] = t;//则用t号L型骨牌覆盖此棋盘的右下角(覆盖这三个较小的棋盘的汇合处)
chessBorad(tr + s,tc + s,tr + s,tc + s,s);//在对其进行特殊方格的棋盘覆盖
}
}合并排序算法
将待排元素分成大小大致相同的2个子集合,分别对2个子集合进行排序(此操作无限递归)最终将排好序的子集合并成为所要求的排好序的集合。
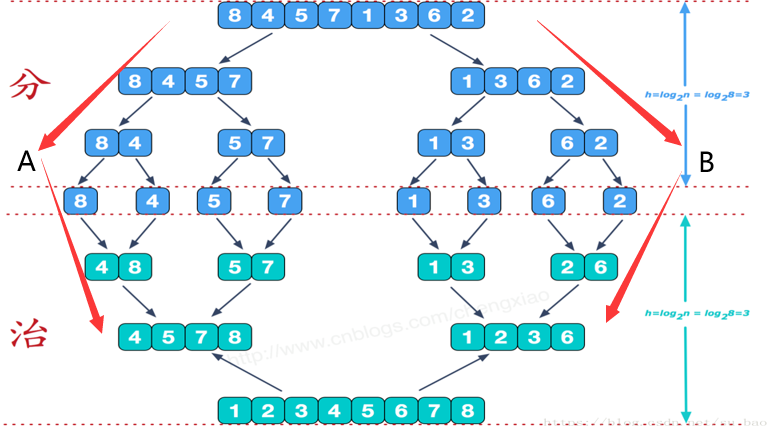
先利用递归将原序列无限划分,直至每一个数组(每个数组均有序)仅由一个元素组成。之后相邻数组进行合并,逐项进行比较,优先将小的值放入合并数组。
例如对【4,8】与【5,7】进行合并时,首先比较4与5,4放入,在比较8与5,5放入,在比较8与7,7放入,最后放入8
public static int[] mergesort(int arr[]){
//如果数组的长度为1,则递归结束
if (arr.length <= 1){
return arr;
}
int mid = arr.length / 2;//数组的中间值
int []left = Arrays.copyOfRange(arr,0,mid);//左半部分数组
int []right = Arrays.copyOfRange(arr,mid,arr.length);//右半部分数组
//mergesort(left);左半部分无限递归
//mergesort(right);右半部分无限递归
return merge(arr,mergesort(left),mergesort(right));//合并操作
}public static int[] merge(int arr[],int [] left,int [] right){
//left的数组的下标
int i = 0;
//right数组的下标
int j = 0;
int m=0;
while (i < left.length && j < right.length) {
nums[m++] = left[i] < right[j] ? left[i] : right[j++];
}
while (i < left.length)//right数组先比较完了,直接将剩余的left数组放进去
nums[m++] = left[i++];
while (j < right.length)//left数组先比较完了,直接将剩余的right数组放进去
nums[m++] = right[j++];
return arr;
}python实现:
def mergeSort(arr):
#递归结束条件
n = len(arr)
if n < 2:
return arr
#中值
middle = n // 2
#取序列的左边部分
left = arr[:middle]
#取序列的右半部分
right = arr[middle:]
#对左侧序列进行递归,分离
left_sort = mergeSort(left)
#对右侧序列进行递归,分离
right_sort = mergeSort(right)
#左右两侧实行合并
return merge(left_sort,right_sort)
def merge(left,right):
#合并数组
res = []
while (len(left) > 0) and (len(right) > 0):
#执行,每比较一次,就将较小值取出放入合并数组,故长度为循环条件
#同时保证,保证左右两边始终可以比较
if left[0] <= right[0]:
res.append(left.pop(0))#将left的第一个元素移除放入合并数组,因此每次均是第一项与另一侧第一项进行比较
else:
res.append(right.pop(0))
if left:#表示right已经完全放入合并数组,此时left有剩余,并且有序,直接放入合并数组即可
res.extend(left)
if right:
res.extend(right)
return res逆序对的个数
给定一个随机数数组,求取这个数组中的逆序对总个数。
合并排序算法中,合并的过程,相邻数组进行比较,因此只需在左侧大于右侧(逆序对)的位置计数即可
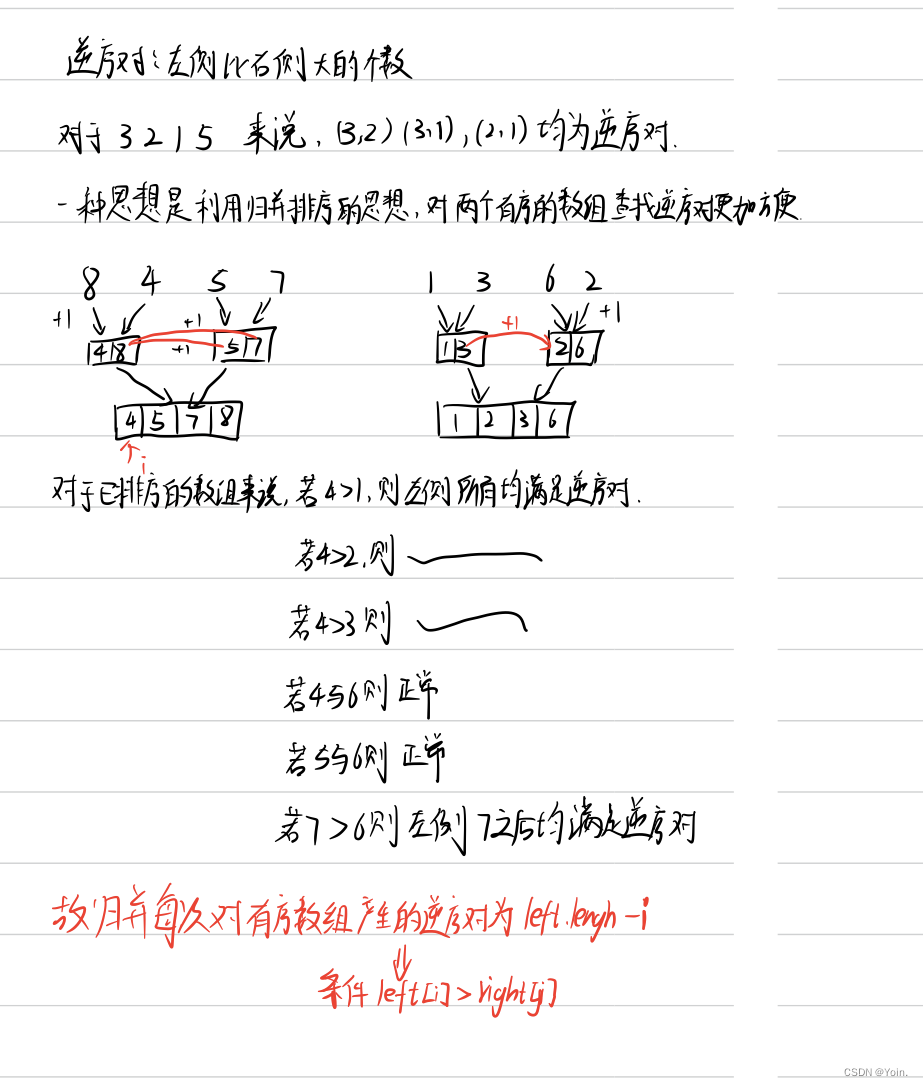
public static int[] mergesort(int arr[]){
//如果数组的长度为1,则递归结束
if (arr.length <= 1){
return arr;
}
int mid = arr.length / 2;//数组的中间值
int []left = Arrays.copyOfRange(arr,0,mid);//左半部分数组
int []right = Arrays.copyOfRange(arr,mid,arr.length);//右半部分数组
return merge(arr,mergesort(left),mergesort(right));//合并操作
}
static int sum = 0;
public static int[] merge(int arr[],int [] left,int [] right){
//left的数组的下标
int i = 0;
//right数组的下标
int j = 0;
for (int index = 0;index < arr.length;index++){
if (i >=left.length){//left数组先比较完了,直接将剩余的right数组放进去
arr[index] = right[j++];
} else if (j>=right.length){//right数组先比较完了,直接将剩余的left数组放进去
arr[index] = left[i++];
} else if (left[i] < right[j]){
arr[index] = left[i];
i++;
} else {
arr[index] = right[j];
j++;
sum=sum+(left.length - i);
}
}
return arr;
}去递归的合并排序算法
将数组中的元素看作分散的单个数组,而不是利用递归划分成子问题,每个元素变成一个数组

public static void mergeSort(int []a){
int []b = new int[a.length];
int s = 1;
while (s < a.length){
mergePass(a,b,s);//合并到b数组,长度变为2倍
s+=s;
mergePass(b,a,s);//合并到a数组,长度变为2呗
s+=s;
}
}
public static void mergePass(int []x,int []y,int s){//s为数组的长度
int i = 0;
while (i <= x.length - 2 * s){//当i=x.length - 2 * s时,说明待合并的数组就还剩两个,长度为2s
//合并大小为s的相邻的2个子数组
merge(x,y,i,i + s - 1,i + 2 * s - 1);//i + s - 1第一个数组的末尾,i + 2 * s - 1第二个数组的末尾
i = i + 2 * s;//下一个相邻数组的初始位置
}
//剩下的元素少于2s
if (i + s < x.length) merge(x,y,i,i+s-1,x.length-1);
else {//就剩余了一个数组
for (int j = i;j<x.length;j++) y[j]=x[j];
}
}
public static void merge(int[] c,int[] d,int l,int m,int r) {
//合并c[l:m]和c[m+1:r]到d[l:r]
int i = l;
int j = m + 1;
int k = l;
while ((i <= m)&&(j <= r)){
//将小的值存入数组
if (c[i] <= c[j]){
d[k++] = c[i++];
}
else d[k++] = c[j++];
//左数组完全放入,右数组有剩余,直接将右数组剩余部分放入数组
if (i > m){
for (int q = j;q<=r;q++) d[k++] = c[j];
}
else {
for (int q = i;q <= m;q++) d[k++] = c[i];
}
}
}快速排序算法
1、分解
以a[p]为基准元素(可用随机基准元素提高随机性)将a[p:r]划分为3段a[p:q-1] , a[q] , a[q+1,r] 三段,使得a[p:q-1] (内部无序) 中的任何元素小于i等于 a[q] , a[q+1,r] (内部无序)中的任何元素大于等于a[q]。
2、递归求解
通过递归调用快速排序算法,分别对a[p:q-1] 和 a[q+1,r] 进行分解排序,无限细分下去,直至只剩一个元素,初始指针与末尾指针直接相等。
3、合并
通过步骤得到的序列已经是排好序的,直接将左右两边拼接到一起即可

private static void quickSort(int[] nums,int start,int end) {
if (start>=end) return;
int pivot = nums[start];
int i=start;
int j=end;
while(i < j){
while (nums[j]>pivot&&i<j) j--;//右哨兵先走,
while (nums[i]<=pivot&&i<j) i++;
//以上两个循环找到左侧比pivot大的与右侧比pivot小的
swap(nums,i,j);
}//此循环将比pivot大的分一组,小的分一组
//最终位置,因为右哨兵先走,j最终指向最后一个小于pivot的元素
swap(nums,start,j);//将基准值弄到中间来
quickSort(nums,start,j-1);
quickSort(nums,j+1,end);
}找出数组中第K小的值(快速排序算法)
首先利用快速排序算法将数组分成以基准值为分界的两组数,若基准值的下标等于k则找到;若基准值的下标大于k,则在基准值左侧寻找;若基准值的下标小于k,则在基准值右侧寻找。

private static int select(int[] nums, int k) {
int start=0;
int end=nums.length-1;
return quick(nums,start,end,k);
}
private static int quick(int[] nums, int start, int end, int k) {
if (k>end) return -1; //大于长度直接返回-1
int pivot=nums[start];
int i=start;
int j=end;
while (i<j){
while (nums[j]>pivot&&i<j) j--;
while (nums[i]<=pivot&&i<j) i++;
swap(nums,i,j);
}
swap(nums,start,j);//将基准值弄到中间来
if (k<j+1) return quick(nums,start,j-1,k);//基准值左侧
else if (k==j+1) return nums[j];
else if(k>j+1) return quick(nums,j+1,end,k);//基准值右侧
return -1;
}







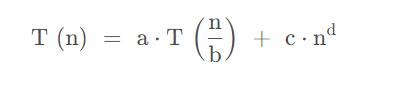
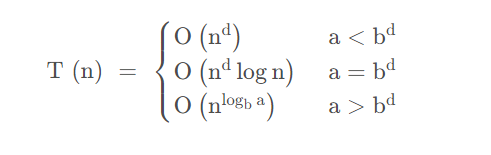
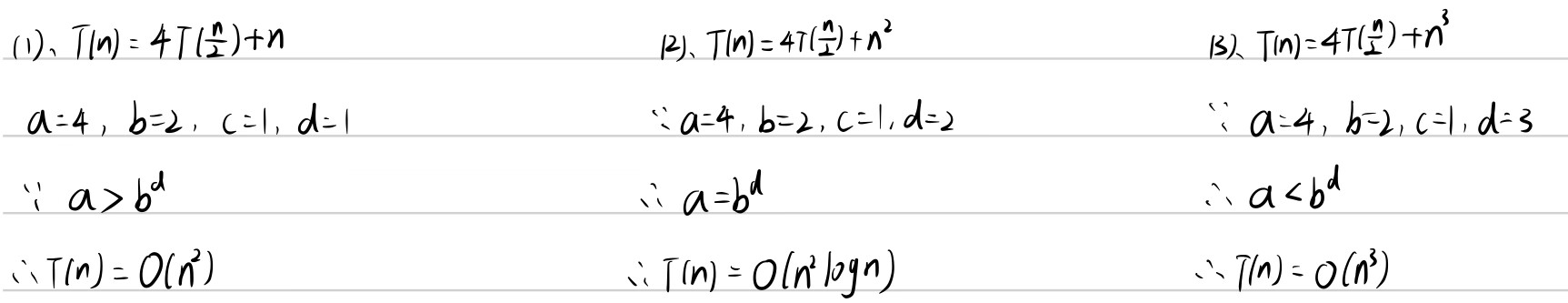














 903
903











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










