acwing788. 逆序对的数量

给定一个长度为 n 的整数数列，请你计算数列中的逆序对的数量。

逆序对的定义如下：对于数列的第 i 个和第 j 个元素，如果满足 i<j 且 a[i]>a[j]，则其为一个逆序对；否则不是。

输入格式
第一行包含整数 n，表示数列的长度。

第二行包含 n 个整数，表示整个数列。

输出格式
输出一个整数，表示逆序对的个数。

数据范围
1≤n≤100000，
数列中的元素的取值范围 [1,10^9]。
输入样例：
6
2 3 4 5 6 1
输出样例：
5

暴力做法：超时

#include <iostream>

using namespace std;

const int N = 100010;
int n;
int a[N];

int main()
{
    long long re = 0;
    cin >> n;
    for(int i =0; i < n; i ++) cin >> a[i];
    for(int i =0; i < n; i ++)
        for(int j = i; j < n; j ++)
            if(a[i] > a[j]) re ++;
    
    cout << re;
    return 0;
}

思路： 分治思想

首先我们给出逆序对的定义：
对于数列的第 i 个和第 j 个元素，如果满足 i < j 且 a[i] > a[j]，则其为一个逆序对。
重要的地方在于，一个元素可以不只是在一个逆序对中存在。如果 k > j > i 且 a[i] > a[j] > a[k]，那么这里
有两个含 a[i] 的逆序对，分别是 (a[i], a[j]) 和 (a[i], a[k]), a[i]是可以使用多次的。

那么第二步是分析问题，这里我们可以使用分治法解决问题。

我们将序列从中间分开，将逆序对分成三类：

1. 两个元素都在左边；
2. 两个元素都在右边；
3. 两个元素一个在左一个在右；

因此这就是我们算法的大致框架：

计算逆序对的数量（序列）：

1. 递归算左边的；
2. 递归算右边的；
3. 算一个左一个右的；
4. 把他们加到一起。

这个时候我们注意到一个很重要的性质，左右半边的元素在各自任意调换顺序，是不影响第三步计数的，因此我们可以数完就给它排序。这么做的好处在于，如果序列是有序的，会让第三步计数很容易。
如果无序暴力数的话这一步是O(n^2)的。

比如序列是这样的

4 5 6 | 1 2 3

当你发现 4 比 3 大的时候，也就是说右边最大的元素都小于左边最小的元素，那么左边剩下的5和6都必然比右边的所有元素大，因此就可以不用数5和6的情形了，直接分别加上右半边的元素个数就可以了，这一步就降低到了
O(n), 我们知道递归式 T(n) = 2T(n/2)+O(n) = O(nlogn)的，所以排序的成本是可以接受的，并且这一问题下，
可以很自然地使用归并排序。

下面放上一张图：

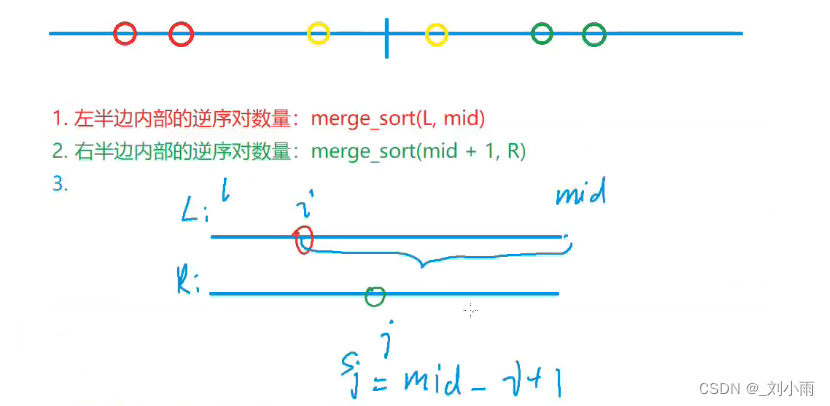
1. 求左边逆序对的数量
2. 求右边逆序对的数量
3. 需要是下面区间，所有点构成逆序对的数量之和， 而因为是有序数列，求出一个点之后，后面依次计算 mid - i + 1
   
   code:

#include <iostream>

using namespace std;
typedef long long LL;

const int N = 100010;
int n;
int a[N], tmp[N];

LL merge_sort(int l, int r)
{
    if (l >= r) return 0;  // 不能忘
    
    int mid = l + r >> 1;
    LL re = merge_sort(l, mid) + merge_sort(mid + 1, r);
    
    // 归并的过程
    int k =0, i = l, j = mid + 1;
    while(i <= mid && j <= r)
    {
        if(a[i] <= a[j]) tmp[k++] = a[i++];
        else
        {
            tmp[k++] = a[j++];
            re += mid - i + 1;
        }
    }
    
    // 扫尾
    while(i <= mid) tmp[k++] = a[i++];
    while(j <= r) tmp[k++] = a[j++];
    
    // 物归原主
    for(int i = l, j = 0; i <= r; i ++, j ++) a[i] = tmp[j];
    return re;
}

int main()
{
    cin >> n;
    for(int i = 0; i < n; i ++) cin >> a[i];
    cout << merge_sort(0, n - 1);
    return 0;
}