chisel格雷码二进制转换

一、格雷码简介

格雷码是一个叫弗兰克*格雷的人在 1953 年发明的，最初用于通信。格雷码是一种循环二进制码或者叫作反射二进制码。格雷码的特点是从一个数变为相邻的一个数时，只有一个数据位发生跳变，由于这种特点，就可以避免二进制编码计数组合电路中出现的亚稳态。格雷码常用于通信，FIFO 或者 RAM 地址寻址计数器中。

格雷码属于可靠性编码，是一种错误最小化的编码方式，因为虽然二进制码可以直接由数/模转换器转换成模拟信号，但在某些情况，例如从十进制的 3 转换为 4 时二进制码的每一位都要变，能使数字电路产生很大的尖峰电流脉冲。而格雷码则没有这一缺点，它在相邻位间转换时，只有一位产生变化。它大大地减少了由一个状态到下一个状态时逻辑的混淆。

二进制计数编码从 0 到 15 的计数过程如下：

从上面的对应关系可以看出，当数字从 7 变为 8 时，4 位二进制数都发生跳变，如果直接使用异步时钟采样这些数字信号，这就很可能会发生亚稳态或者数据采样错误。而采用格雷码，就可以避免 4 位二进制数都同时发生跳变，就算出现亚稳态，最多也就一位出现错误。

二、互相转换原理

一般数字设计里面都是使用二进制码，那么我们想使用格雷码需要怎么转换呢？这就涉及到格雷码和二进制码互相转换的问题。我们先来看下格雷码如何转换到二进制码。

格雷码转化为二进制码原理如下：

使用格雷码的最高位作为二进制的最高位，二进制次高位产生过程是使用二进制的高位和次高位格雷码相异或得到，其他位的值与次高位产生过程类似。假设二进制和格雷码各个位分别使用如下字符表示：

n 位的二进制：Bn, Bn-1, Bn-2。。。B2, B1 , B0;
n 位的格雷码：Gn, Gn-1, Gn-2。。。G2, G1, G0;

转换公式：

Bn =Gn；
Bi-1 = Bi ^ Gi-1；( i=1,2,n-1; )

其运算过程的示意图如下图所示（这里以 4 位的数据位宽为例）：

从图中可以看出，二进制最高位和格雷码最高位相同，都是 1，次高位为二进制的高位和次高位格雷码相异或得到，即 bit2 为 0=1^1。

---

介绍完格雷码如何转换到二进制后，我们再来看下二进制码如何转换到格雷码。

二进制码转化为格雷码原理如下：

二进制的最高位作为格雷码的最高位，次高位的格雷码为二进制的高位和次高位相异或得到，其他位与次高位类似。假设二进制和格雷码各个位分别使用如下字符表示：

n 位的二进制：Bn, Bn-1,Bn-2。。。B2,B1,B0;
n 位的格雷码：Gn, Gn-1,Gn-2。。。G2,G1,G0;

转换公式：
Gn = Bn；
Gi-1=Bi ^ Bi-1； ( i=1,2,n-1; )

其运算过程的示意图如下图所示（这里以 8 位的数据位宽为例）：

从图可以很容易的看出，二进制码右移 1 位后与本身异或，其结果就是格雷码。从最右边一位起，依次将每一位与左边一位异或（XOR），作为对应格雷码该位的值，最左边一位不变。

三、设计代码

package simple

import chisel3._
import chisel3.util._
import chisel3.stage._
import scala.collection._

// create a module
class GrayCoder(bitwidth: Int) extends Module {
  val io = IO(new Bundle{
    val in = Input(UInt(bitwidth.W))
    val out = Output(UInt(bitwidth.W))
    val encode = Input(Bool()) // decode on false
  })
  
  when (io.encode) { //encode 二进制转格雷码
    io.out := io.in ^ (io.in >> 1.U)
  } .otherwise { // decode 格雷码转二进制
    
    //val seq = mutable.ArrayBuffer[UInt]()
    //var seq = List[UInt]()
    var seq = List.fill(bitwidth - 1)(0.U(1.W))

    for (i <- 0 until bitwidth - 1){
      //seq += io.in(i)
      //seq = io.in(i) +: seq
      seq = io.in(i) +: seq.take(bitwidth - 1 - 1)
    }
    
    val out = seq.scan(io.in(bitwidth - 1))(_ ^ _) //从高到低顺序的结果，不过是list

    //必须转成bool才能进行单bit赋值
    //io.out := DontCare
    val bools = VecInit(io.out.asBools)
    
    for (i <- 0 until bitwidth){ 
      bools(bitwidth- 1 - i) := out(i).asBool//out(i)是UInt(1.W)
      
    }
    io.out := bools.asUInt
  }
  
  
}


// Generate the Verilog code
object GrayCoderMain extends App {
    println("Generating the GrayCoder hardware")
    
    (new chisel3.stage.ChiselStage).execute(Array("--target-dir", "generated"), Seq(ChiselGeneratorAnnotation(() => new GrayCoder(4))))
}

四、测试代码

package simple

import chisel3._
import chisel3.util._
import chiseltest._
import chiseltest.RawTester.test
import scala.math.pow

object GrayCoderTester extends App {
    // test our gray coder
    val bitwidth = 4


    test(new GrayCoder(bitwidth)) { c =>
        def toBinary(i: Int, digits: Int = 8) = {
            String.format("%" + digits + "s", i.toBinaryString).replace(' ', '0')
        }
        println("Encoding:")
        for (i <- 0 until pow(2, bitwidth).toInt) {
            c.io.in.poke(i.U)
            c.io.encode.poke(true.B)
            c.clock.step(1)
            println(s"In = ${toBinary(i, bitwidth)}, Out = ${toBinary(c.io.out.peek().litValue.toInt, bitwidth)}")
        }

        println("Decoding:")
        for (i <- 0 until pow(2, bitwidth).toInt) {
            c.io.in.poke(i.U)
            c.io.encode.poke(false.B)
            c.clock.step(1)
            println(s"In = ${toBinary(i, bitwidth)}, Out = ${toBinary(c.io.out.peek().litValue.toInt, bitwidth)}")
        }

    }
}

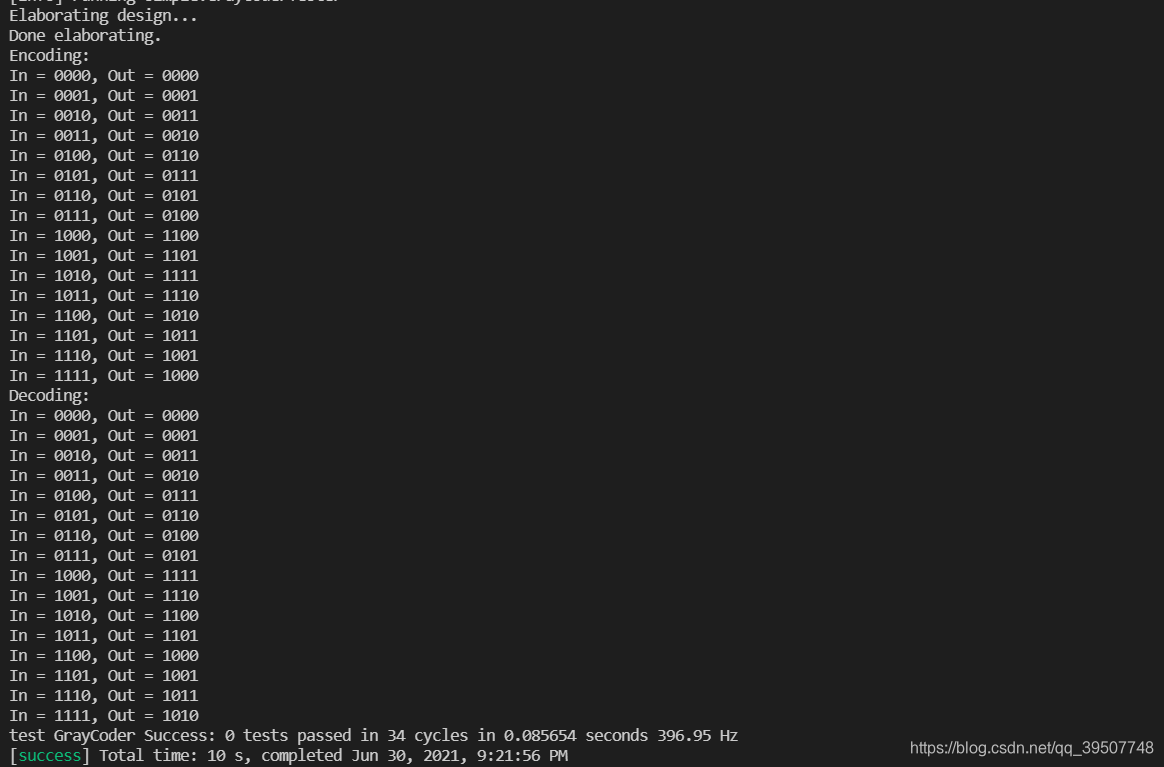
测试结果：