背景
最近做 李飞飞 CS231N 2019 的作业时遇到了问题,具体是assignment1中的features.ipynb中的Neural Network on image features小节,训练一个 用于图片分类的两层神经网络 (结构不重要所以不再展示),要求测试集准确率达到55%(作业提示最高可达60%)。
之前要求训练模型的作业都会预先给出 学习率 α 和 正则化强度 λ 的几个参考值或范围,但这次没有给。我刚开始因为设置了错误的超参数范围,模型的验证集准确率一直在10%左右(该模型的任务是分辨图片属于10个给定类别中的哪一个,10%相当随机选择,已经相当差了),代价曲线也没看出问题,直到参考了其他人的代码才知道 α 和 λ 的范围错了,于是我就开始思考 如何才能快速确定超参数的合适范围?
正文
模型的结构、功能和数据集不同,会导致 合适的超参数范围相差很大 (几个数量级),如果只是 随机尝试或者凭感觉走 ,效率会很低。可视化工具 + 清晰的思路 对于简单和复杂模型的调试都很重要。
用可视化辅助调参
- 方法一:之前在调超参数时,总是简单地用 print函数 打印出每个模型的验证集准确率和它的超参数(α、λ等)的值,重复的文字太多,很不直观

- 方法二:使用 print 函数格式化输出,以 表格 的形式输出。虽然理论上完全可以,但还是有缺点:不够直观、单独编程比较麻烦

excel 示意图 - 方法三(最佳方案) 使用 像素 表示单元格中的数据,使用 plt.scatter函数 绘制 散点图 (此处参考了assignment1/svm.ipynb中的用法)并用 plt.annotate函数 在图中 标记出准确率最高的点 ,效果如下:

散点图
每个点代表一个模型的验证集准确率,横、纵坐标分别是其对应的学习率 α 、正则化强度 λ 。右边的 颜色条 显示了准确率大小与点的颜色的对应关系,可以看出准确率越高,点的颜色越红。黄色标签所指的点代表的就是目前的 最佳模型 ,标签显示了它的 lr、reg和准确率。
python代码实现如下,其中results是一个字典,索引是 lr 和 reg ,键值是训练集和验证集的准确率;best_point存储了最优模型的 lr、 reg坐标
# Visualize validation accuracies
# results[(lr, reg)] = (train_acc, val_acc)
# best_point = (math.log10(lr), math.log10(reg)) # for labeling
x_scatter = [math.log10(x[0]) for x in results]
y_scatter = [math.log10(x[1]) for x in results]
marker_size = 100 # default: 20
colors = [results[x][1] for x in results] # depend color on val_acc
plt.figure()
plt.scatter(x_scatter, y_scatter, marker_size, c=colors, cmap=plt.cm.coolwarm)
plt.annotate('(%.2f,%.2f,%.2f%%)'% (best_point[0],best_point[1],best_acc*100),
xy=best_point, xytext=(-30, 30), textcoords='offset pixels',
bbox=dict(boxstyle='round,pad=0.5', fc='yellow', alpha=0.5),
arrowprops=dict(arrowstyle = '->', connectionstyle='arc3,rad=0'))
plt.colorbar()
plt.xlabel('10^lr')
plt.ylabel('10^reg')
plt.title('CIFAR-10 validation accuracy')
plt.show()
关于用法:plt.scatter 中可以通过改变颜色样式和点的大小等等, plt.annotate中xytext、textcoords决定标签的位置、bbox决定边框、arrowprops决定箭头等等,具体的用法自行查阅即可。
调试过程
1. “浅迭代”&“广撒网”
-
“浅迭代”
为了加快速度,一开始尽量将迭代次数设置的少一点,等找到合适的超参数范围之后再增加迭代次数来 “ 冲刺 ” 到更高的准确率,这里我设置为300(即每个模型执行300次梯度下降) -
“广撒网”
由于刚开始不知道 α 和 λ 的大概范围,因此 范围要足够大 ,这里在 [ 1 0 − 10 10^{-10} 10−10 , 1 0 10 10^{10} 1010] 之间取出 5 个数(建议奇数,为了速度先取少一点)组成 等比数列 作为 α 和 λ 的候选值
lr_range = np.logspace(-10, 10, num=5)
reg_range = np.logspace(-10, 10, num=5)
运行结果就是上一张图,这里再贴一下:

图中只有两个红色的点还可以,其余的都很低,最高验证集准确率为 54.40%(目标是测试集达到55%甚至60%) 。
2. 缩小范围&增加候选点密度
上图中,从 x轴 (代表学习率 α ,程序中的 lr )方向上看: 红点 的分布范围很窄,因此考虑将 x 轴范围缩小到 [ 1 0 − 5 10^{-5} 10−5 , 1 0 5 10^{5} 105] ;从 y 轴(正则化强度 λ ,程序中的 reg )方向看:红点的分布出现 触底 ,可以在收缩上限的同时扩展下限,即将 y 轴改为 [ 1 0 − 12 10^{-12} 10−12 , 1 0 0 10^{0} 100]
lr_range = np.logspace(-5, 5, num=5)
reg_range = np.logspace(-12, 0, num=5)
运行结果:

可以看到红点增加了,此时最高准确率为 54.00% 。
再次缩小 lr 范围至** [ 1 0 − 3 10^{-3} 10−3 , 1 0 2 10^{2} 102]**,将 reg 改为 [ 1 0 − 12 10^{-12} 10−12 , 1 0 0 10^{0} 100],考虑到红点的分布还是很窄,使用 增加候选点密度 的方法:将 reg (y轴)的候选点个数加到 7 个:
lr_range = np.logspace(-3, 2, num=5)
reg_range = np.logspace(-12, 0, num=7)
运行结果:

虽然最高准确率反而下降了2%, 但并没有关系。现在的目的只是为了确定一个合适的范围,迭代次数比较少,所以会出现较大的波动。
接下来,按照上述思路交替使用 缩小范围 和 增加候选点 的方法,使得红色和蓝色各自代表的准确率的差值尽可能小,此时说明找到了合适的超参数范围,如图:

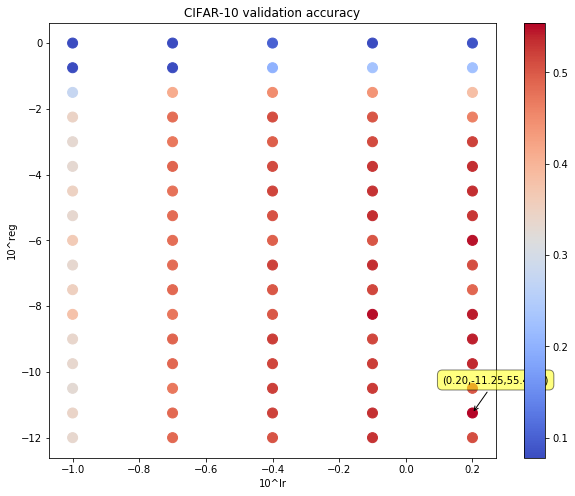

最终调整好的范围如下图,此时最高验证集准确率为 55.40%,可以看出最好(55%)和最差(44%)之间的差距已经缩小至 11% ,说明已经找到了比较合适的超参数范围。

3. “深入迭代”
找到超参数合适的取值范围之后,将迭代次数从 300 增加到 2000 ,此时最高验证集准确率达到了 60.60% ,并且最好的和最差的之间的差距仍然不大:

最后在测试集上运行最佳模型,达到了 58.70% 的准确率,虽然离60%还差点,不过已经达到了55%的要求。如果想追求更高的准确率,也可以继续尝试增加点密度、迭代次数,当然运算时间会更长,还可以选择其他梯度下降算法。

写在最后
-
这次调试的过程让我对 梯度下降 过程有了 更直观的理解——如果把 梯度下降类比成下山 的过程(当然真实情况是比三维复杂的多的高维空间),我们的目的就是到达整片山岭中 海拔最低 的位置。散点图中每个点都是一个 山谷(局部最优解),训练的目的就是 在这些山谷中找出最深的那个 。迭代次数300时的最优解不一定是1500时的最优解,这是因为迭代次数相当于朝着山下走的步数 ,在没有到达山谷的底部之前我们并不知道山谷有多深。
-
虽然本文针对的是简单的两层神经网络,并且散点图有一些缺点(例如因为是二维图像,只能同时调节两个参数),但我相信 可视化工具 和 清晰的思路 这两个核心思想对于层数更多、结构更复杂、参数更多、训练时间更长的 深层神经网络 来说也将会是很重要的。
-
最后,这是我的第一篇博客,处女座的处女作。欢迎评论、转载和收藏,希望能帮到更多的人!
























 749
749

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








