二叉排序树 分析、梳理、代码总结

二叉排序树（binary sort tree）

二叉排序树的定义

    二叉排序树或是一棵空树，或是具有如下性质的非空二叉树：

      (1)若它的左子树非空，则其左子树所有结点的关键字值均小于其根结点的关键字值

      (2)若它的右子树非空，则其右子树所有结点的关键字值均大于其根结点的关键字值

      (3)它的左右子树也分别为一棵二叉排序树

二叉排序树的重要特征：对二叉排序树进行中序遍历可以得到一个关键字有序的序列

二叉排序树的存储：二叉链表

/*二叉排序树的二叉链表存储结构*/
typedef struct BTNode{
    Elemtype key;                       /*记录的关键字，忽略记录的其他数据项*/
    struct BTNode *lchild,*rchild;  
}BTNode,*BSTree;

二叉排序树的查找:

    二叉排序树不空的时候，将给定值key和结点的关键字比较，相等查找成功，小于查找左子树，大于查找右子树，返回空查找失败。

    查找过程实际上是从根结点到结点的路径，即该层的深度。

/*二叉排序树的查找*/
BTNode *SearchBST(BSTree T,int key)      /*T指向二叉排序树的根结点*/
{
    if(T==NULL)                     /*空树，查找失败*/
        return NULL;
    if(key==T->key)             /*查找成功*/
        return T;
    if(key<T->key)
        return SearchBST(T->lchild,key);        /*查找左子树*/
    if(key>T->key)
        return SearchBST(T->rchild,key);       /*查找右子树*/
}

二叉排序树的插入

    插入结点的条件：查找不成功

    基本思想：(1)若二叉排序树为空，则新结点作为二叉排序树的根结点

                     (2)若给定结点的关键字的值小于根结点的值，插入到左子树中

                     (3)若给定结点的关键字的值大于根结点的值，插入到右子树中

/*二叉排序树的插入*/
BSTree InsertBST_key(BSTree T,int key)
{/*在以T为根结点的二叉排序树上查找关键字为key的记录，若不存在将其插入*/
    BTNode *s=SearchBST(T,key);
    if(s!=NULL)
    {
        printf("\n关键字%d已存在！\n",s->key);
        return T;
    }
    s=(BTNode *)malloc(sizeof(BTNode));         /*生成一个结点空间*/
    if(s==NULL)
        printf("Error\n");
    s->key=key;
    s->lchild=s->rchild=NULL;
    T=InsertBST(T,s);               /*在二叉排序树上插入该结点*/
    return T;
}

/*在二叉排序树上插入一个结点*/
BSTree InsertBST(BSTree T,BTNode *s)
{  /*在以T为根的二叉树上插入一个指针s所指向的结点并返回根指针T*/
    if(T==NULL)         /*如果T是空树，则新插入的结点S作为新的树根*/
        T=s;
    else
    {
        if(s->key<T->key)
            T->lchild=InsertBST(T->lchild,s);       /*递归插到T的左子树中*/
        if(s->key>T->key)
            T->lchild=InsertBST(T->lchild,s);        /*递归插到T的右子树中*/
    }
    return T;
}

二叉排序树的创建

    二叉树的创建过程实际上就是一个查找插入的过程，每次插入的新结点都是二叉树上新的叶子结点，操作时不必像静态查找移动其他结点，只需改动新叶子结点的父结点的左或右指针，由空变为非空即可。二叉排序树既拥有类似折半查找的特性，又采用链表作为存储结构。

/*二叉排序树的创建*/
BSTree CreateBST()      /*由空树开始，输入关键字序列，建立一棵二叉排序树*/
{
    BSTree T=NULL,s=NULL;
    int key;
    printf("输入关键字序列，输入-1结束\n");
    while(1)
    {
        scanf("%d",&key);     
        if(key==-1)
            break;
        s=(BTNode *)malloc(sizeof(BTNode));         /*生成一个结点空间*/
        s->key=key;
        s->lchild=s->rchild=NULL;
        T=InsertBST(T,s);                   /*在二叉排序树中插入该结点*/
    }
    return T;
}

二叉排序树的删除

    假设待删除的结点为*p，f指向结点*p的双亲，s指向*p的左子树中关键字值最大的结点，q指向s的双亲

    删除分为3中情况：

      (1)*p为叶子结点，即其左右结点为空-----将其双亲结点f的lchild或rchild置空，删除结点

      (2)*p只有一棵非空子树（左子树或右子树）

           只有左子树-----用左子树的根结点取代要删除的结点

           只有右子树-----用右子树的根结点取代要删除的结点

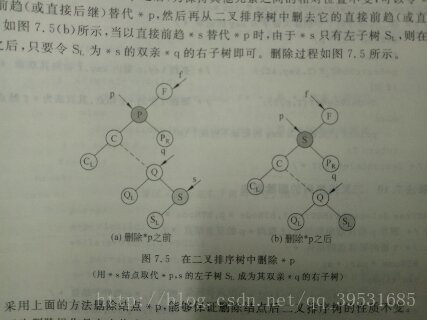
      (3)*p左右子树均非空-----用*p左子树中关键字最大的结点*s替代*p，若*s有左孩子，将左孩子作为*s的双亲结点*q的右孩子  

                                             

    为了删除结点后重接子树，要修改查找算法

/*为了删除操作而修改的二叉排序树查找*/
BTNode *SearchBST_F(BSTree T,int key,BSTree *F)
{   /*T指向根结点，*F存储指向key的双亲的指针*/
    /*查找成功，返回指向key的记录指针，查找失败返回NULL*/
    if(T==NULL)
        return NULL;
    if(key==T->key)
        return T;
    *F=T;
    if(key<T->key)
        return SearchBST_F(T->lchild,key,F);
    if(key>T->key)
        return SearchBST_F(T->rchild,key,F);
}

/*在二叉排序树中查找并删除关键字为key的记录*/
BSTree SearchDeleteBST(BSTree T,int key)
{
        BTNode *f=NULL,*pNULL;
        p=SearchBST_F(T,key,&f);        /*查找key，p指向key，f指向双亲*/
        if(p!=NULL)
            T=DeleteBST(T,p,f);
        else
            printf("关键字为key的记录不存在！\n");
        return T;
}

二叉排序树的删除算法

/*二叉排序树的删除*/
BSTree DeleteBST(BSTree T,BTNode *p,BTNode *f)
{/*删除p指针指向的结点，f指向*p的双亲结点*/
 /*T是指向根结点的指针*/
    BTNode *par,*s;
    int kind;
    if(p->lchild==NULL&&p->rchild==NULL)            /*情况1,*p为叶子结点*/
        kind=1;                                                 
    else if(p->rchild==NULL)                /*情况2,*p只有左子树*/
        kind=2; 
    else if(p->lchild==NULL)                /*情况3,*p只有右子树*/
        kind=3;
    else                                                    /*情况4，*p左右子树非空*/
        kind=4;
    switch(kind)
    {
        case 1:    if(f==NULL)         /*p指向根结点，树中只有根结点*/
                                T=NULL;             /*删除结点*p，T变空树*/
                        else
                        {
                                if(f->lchild==p)       /* *p是*f的左孩子*/
                                    f->lchild=NULL;
                                else                           /* *p是*f的右孩子*/
                                    f->rchild==NULL;       
                        }
                        free(p);                       /*删除结点释放空间*/
                        break;
        case 2:    if(f==NULL)          /*f为NULL，*p为根结点，且只有左子树*/
                                T=p->lchild;
                        else
                        {
                            if(f->lchild==p)       /* *p是*f的左子树*/
                                f->lchild=p->lchild;
                            else                         /* *p是*f的右子树*/
                                f->rchild=p->lchild;
                        }
                        free(p);                       /*删除结点释放空间*/
                        break;
        case 3:     if(f==NULL)        /*f为NULL，*p为根结点，且只有左子树*/
                                T=p->rchild;
                           else
                           {
                               if(p==f->lchild)
                                    f->lchild=p->rchild;
                               else
                                    f->rchild=p->rchild;
                           }
                           free(p);
                           break;
        case 4:     par=p;
                          s=p->lchild;
                          while(s->rchild!=NULL)        /*找到p左子树的关键字最大（最右下）的结点*/
                          {
                              par=s;
                              s=s->rchild;
                          }
                          p->key=s->key;        /*s结点的值覆盖p结点的值*/
                          if(par==p)           /*处理特殊情况，*p的左孩子为*s*/
                                par->lchild=s->lchild;
                          else
                                par->rchild=s->lchild;      /*s的左子树连接到s的双亲结点作为双亲结点的右子树*/
                          free(s);           /*注意不是free(p)，因为p的关键字被s的关键字覆盖，s已无用*/
    }
    return T;
}

完整代码如下：

#include <iostream>
#include<stdio.h>
#include<malloc.h>
using namespace std;
typedef int Elemtype;
/*二叉排序树的二叉链表存储结构*/
typedef struct BTNode{
    Elemtype key;                       /*记录的关键字，忽略记录的其他数据项*/
    struct BTNode *lchild,*rchild;
}BTNode,*BSTree;

/*二叉排序树的查找*/
BTNode *SearchBST(BSTree T,int key)      /*T指向二叉排序树的根结点*/
{
    if(T==NULL)                     /*空树，查找失败*/
        return NULL;
    if(key==T->key)             /*查找成功*/
        return T;
    if(key<T->key)
        return SearchBST(T->lchild,key);        /*查找左子树*/
    if(key>T->key)
        return SearchBST(T->rchild,key);       /*查找右子树*/
}

/*在二叉排序树上插入一个结点*/
BSTree InsertBST(BSTree T,BTNode *s)
{  /*在以T为根的二叉树上插入一个指针s所指向的结点并返回根指针T*/
    if(T==NULL)         /*如果T是空树，则新插入的结点S作为新的树根*/
        T=s;
    else
    {
        if(s->key<T->key)
            T->lchild=InsertBST(T->lchild,s);       /*递归插到T的左子树中*/
        if(s->key>T->key)
            T->lchild=InsertBST(T->lchild,s);        /*递归插到T的右子树中*/
    }
    return T;
}

/*二叉排序树的插入*/
BSTree InsertBST_key(BSTree T,int key)
{/*在以T为根结点的二叉排序树上查找关键字为key的记录，若不存在将其插入*/
    BTNode *s=SearchBST(T,key);
    if(s!=NULL)
    {
        printf("\n关键字%d已存在！\n",s->key);
        return T;
    }
    s=(BTNode *)malloc(sizeof(BTNode));         /*生成一个结点空间*/
    if(s==NULL)
        printf("Error\n");
    s->key=key;
    s->lchild=s->rchild=NULL;
    T=InsertBST(T,s);               /*在二叉排序树上插入该结点*/
    return T;
}

/*二叉排序树的创建*/
BSTree CreateBST()      /*由空树开始，输入关键字序列，建立一棵二叉排序树*/
{
    BSTree T=NULL,s=NULL;
    int key;
    printf("输入关键字序列，输入-1结束\n");
    while(1)
    {
        scanf("%d",&key);
        if(key==-1)
            break;
        s=(BTNode *)malloc(sizeof(BTNode));         /*生成一个结点空间*/
        s->key=key;
        s->lchild=s->rchild=NULL;
        T=InsertBST(T,s);                   /*在二叉排序树中插入该结点*/
    }
    return T;
}

/*为了删除操作而修改的二叉排序树查找*/
BTNode *SearchBST_F(BSTree T,int key,BSTree *F)
{   /*T指向根结点，*F存储指向key的双亲的指针*/
    /*查找成功，返回指向key的记录指针，查找失败返回NULL*/
    if(T==NULL)
        return NULL;
    if(key==T->key)
        return T;
    *F=T;
    if(key<T->key)
        return SearchBST_F(T->lchild,key,F);
    if(key>T->key)
        return SearchBST_F(T->rchild,key,F);
}

/*二叉排序树的删除*/
BSTree DeleteBST(BSTree T,BTNode *p,BTNode *f)
{/*删除p指针指向的结点，f指向*p的双亲结点*/
 /*T是指向根结点的指针*/
    BTNode *par,*s;
    int kind;
    if(p->lchild==NULL&&p->rchild==NULL)            /*情况1,*p为叶子结点*/
        kind=1;
    else if(p->rchild==NULL)                /*情况2,*p只有左子树*/
        kind=2;
    else if(p->lchild==NULL)                /*情况3,*p只有右子树*/
        kind=3;
    else                                                    /*情况4，*p左右子树非空*/
        kind=4;
    switch(kind)
    {
        case 1:    if(f==NULL)         /*p指向根结点，树中只有根结点*/
                                T=NULL;             /*删除结点*p，T变空树*/
                        else
                        {
                                if(f->lchild==p)       /* *p是*f的左孩子*/
                                    f->lchild=NULL;
                                else                           /* *p是*f的右孩子*/
                                    f->rchild==NULL;
                        }
                        free(p);                    /*删除结点释放空间*/
                        break;
        case 2:    if(f==NULL)          /*f为NULL，*p为根结点，且只有左子树*/
                                T=p->lchild;
                        else
                        {
                            if(f->lchild==p)       /* *p是*f的左子树*/
                                f->lchild=p->lchild;
                            else                         /* *p是*f的右子树*/
                                f->rchild=p->lchild;
                        }
                        free(p);                       /*删除结点释放空间*/
                        break;
        case 3:     if(f==NULL)        /*f为NULL，*p为根结点，且只有左子树*/
                                T=p->rchild;
                           else
                           {
                               if(p==f->lchild)
                                    f->lchild=p->rchild;
                               else
                                    f->rchild=p->rchild;
                           }
                           free(p);
                           break;
        case 4:     par=p;
                          s=p->lchild;
                          while(s->rchild!=NULL)        /*找到p左子树的关键字最大（最右下）的结点*/
                          {
                              par=s;
                              s=s->rchild;
                          }
                          p->key=s->key;        /*s结点的值覆盖p结点的值*/
                          if(par==p)           /*处理特殊情况，*p的左孩子为*s*/
                                par->lchild=s->lchild;
                          else
                                par->rchild=s->lchild;      /*s的左子树连接到s的双亲结点作为双亲结点的右子树*/
                          free(s);           /*注意不是free(p)，因为p的关键字被s的关键字覆盖，s已无用*/
    }
    return T;
}

BSTree SearchDeleteBST(BSTree T,int key)
{
        BTNode *f=NULL,*p=NULL;
        p=SearchBST_F(T,key,&f);        /*查找key，p指向key，f指向双亲*/
        if(p!=NULL)
            T=DeleteBST(T,p,f);
        else
            printf("关键字为key的记录不存在！\n");
        return T;
}


int main()
{

    return 0;
}