动态规划在求解传递闭包问题中的应用（JAVA）--Warshell算法

动态规划在求解传递闭包问题中的应用：

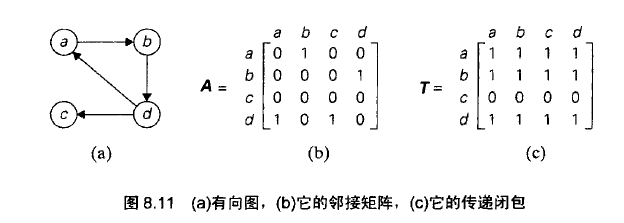
传递闭包：对于n个顶点有向图来说，如果第i个顶点到第j个顶点之间存在一条有效的有向路径（即长度大于0的路径），那么T(i, j) = 1,否则T(i, j) = 0。例如：

求解传递闭包我们可以使用深度优先搜索和广度优先搜索，我们可以对每个顶点进行DFS/BFS，在对应的矩阵位置上置为1，遍历之后我们便得到整个图的传递闭包。

但是这种方式并不是高效的算法，而Warshell算法却能很好的解决问题。

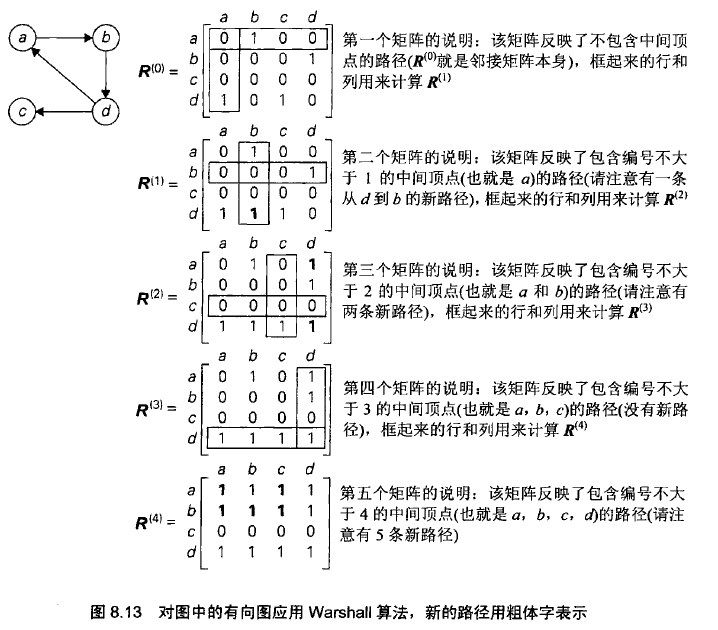
Warshell算法通过一系列n阶布尔矩阵来构造传递闭包 R(0),...R(k),...,R(n) 。其中的每个布尔矩阵都提供有向图中有向路径的特定信息。具体来说，当且仅当从第i个顶点到第j个顶点之间存在一条有向路径，并且路径的每一个中间顶点的编号不大于k时，矩阵中第i行第j列的元素值为1。

R(0)中每个点的含义为：当且仅当从第i个顶点到第j个顶点之间存在一条有向路径，并且路径不存在中间顶点。即该矩阵为图的邻接矩阵。

R(k)中每个点的含义为：当且仅当从第i个顶点到第j个顶点之间存在一条有向路径，并且路径的每一个中间顶点的编号不大于k

R(n)中每个点的含义为：当且仅当从第i个顶点到第j个顶点之间存在一条有向路径，并且路径的每一个中间顶点的编号不大于n，即图的传递闭包。

思路：任何R(k)可以由R(k-1)计算的到的，那么，从第i个顶点vi到第j个顶点vj的路径可以表示为：

vi, ]每个顶点编号<=k的一个中间顶点集]，vj

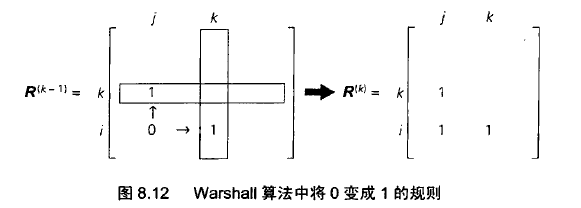
这会存在两种情况，情况一：R(k-1) = 1，中间顶点集中不包含k即可到达vj;

情况二，R(k-1) = 0，中间顶点集必须包含k才能到达vj，那么，只有当矩阵中第i行第k列的元素和第k行第j列的元素都是1，R(k)才能是1。示例如下图：

下面将以示例的形式具体展示Warshell算法的流程：

Input：

4 4

1 2

2 4

4 1

4 3

Output:

1 1 1 1 
1 1 1 1 
0 0 0 0 
1 1 1 1

完整代码如下：

import java.util.Scanner;

public class Main {
    static int[][] e = new int[10][10];
    static int n, m;
    static Scanner input = new Scanner(System.in);

    public static void main(String[] args) {
        n = input.nextInt();
        m = input.nextInt();
        for (int i = 1; i <= m; i++) {
            int a = input.nextInt();
            int b = input.nextInt();
            e[a][b] = 1;
        }
        floyd();
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                System.out.print(e[i][j] + " ");
            }
            System.out.println();
        }
    }
    public static void floyd() {
        for (int k = 1; k <= n; k++) {
            for (int i = 1; i <= n; i++) {
                for (int j = 1; j <= n; j++) {
                    if (e[i][j] != 0) {
                        e[i][j] = 1;
                    } else if (e[i][k]!=0 && e[k][j]!=0) {
                        e[i][j] = 1;
                    }
                }
            }
        }
    }
}

时间复杂度：O(n^3)

更一般的问题是求解带权图中全源最短路径的长度。