[论文笔记]Graph Cube: 基于数据仓库和OLAP多维网络

Graph Cube: On Warehousing and OLAP Multidimensional Networks

研究背景

  数据仓库是一种为企业进行决策制定的工具。区别于数据库，数据仓库的主要功能并非保存数据，而是为数据分析师，战略制定者获取有价值信息提供服务的。

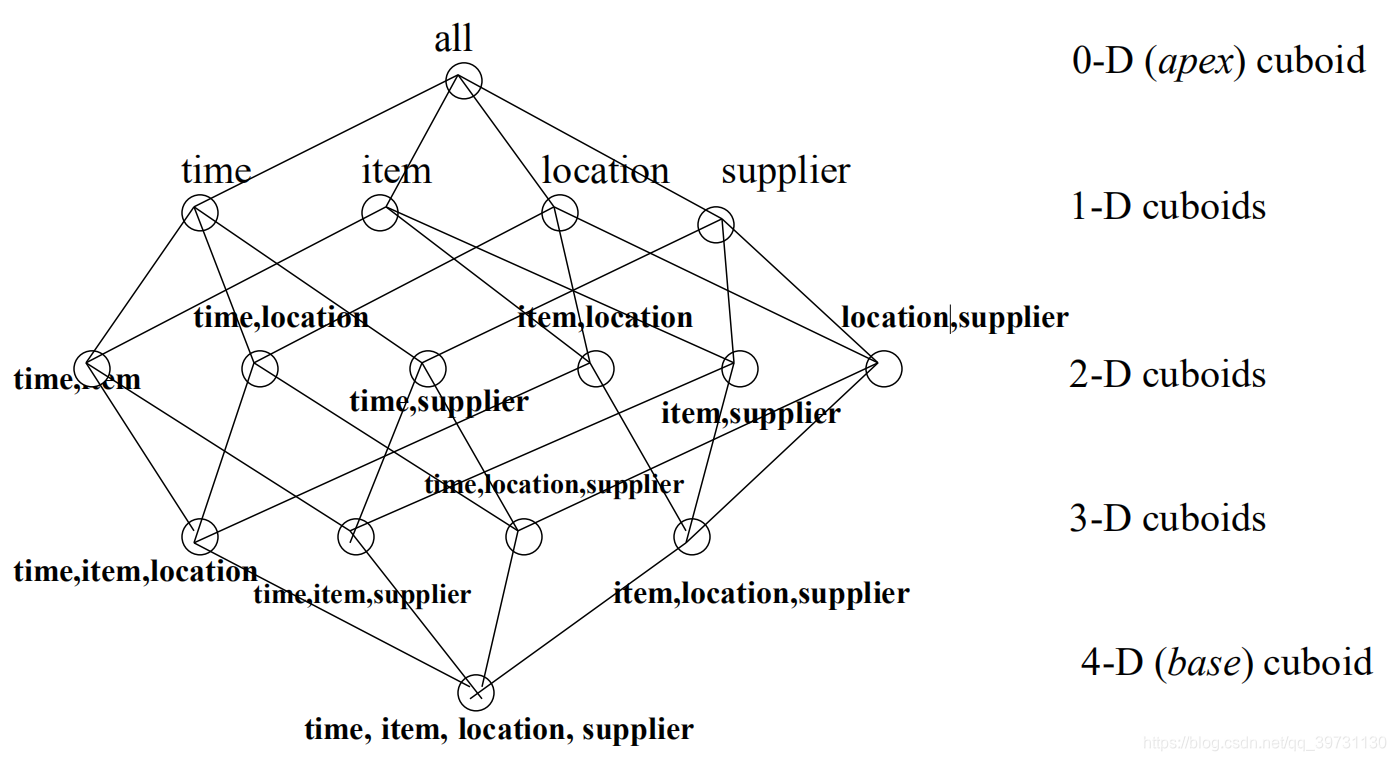
  如上图所示，数据仓库的基本模型是数据立方体(Cube)，数据立方体由多个方体(Cuboid)组成。每个方体可以表示为一张表，属性为方体的维度，表中的每行数据称为元组(Cell)。

  以往人们在使用数据仓库时，总是根据维度需求在数据立方体中计算出单个所需的方体，以便进行数据分析或数据挖掘。然而当我们需要对多个方体进行联合分析时，传统的数据仓库模型便无法做到了。除此之外，传统的方体只关注元组的属性和度量，而忽略了不同元组之间的关系。当我们想分析个体之间的联系时，也是很不方便的。

  作者基于上述问题，提出了新的数据仓库模型——图数据立方体(Graph Cube)，并在此基础上提出了解决多个方体联合分析的方法——跨方体(Crossboid)。

Graph Cube 模型

  首先介绍一下多维网络(Multidimensional Network)。多维网络的示意图如下所示。

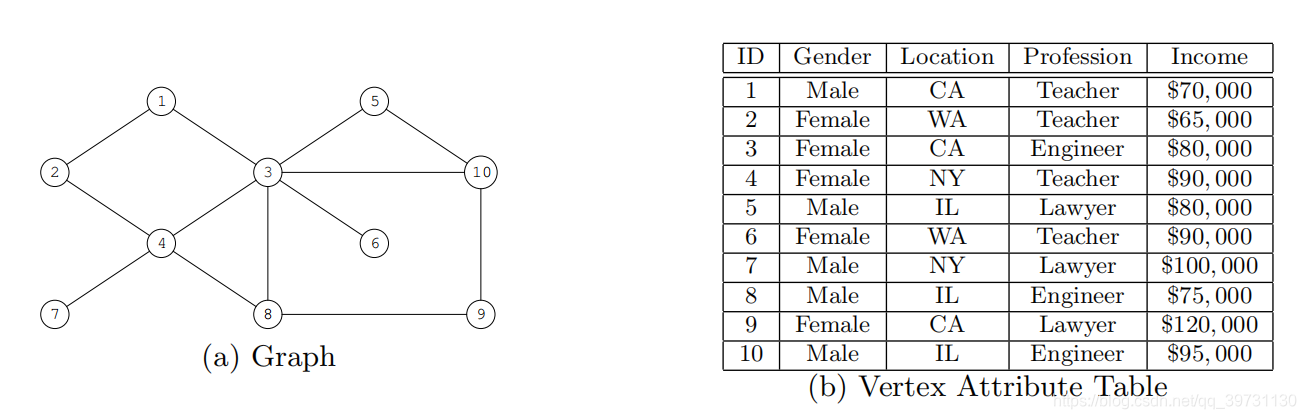
  可以看到，多维网络就是图与表的结合。图中顶点表示单个个体，个体拥有多个属性(ID, Gender, Location, Profession, Income)，其中ID为个体的主键，标记在顶点的内部。图中边表示个体之间的关系。

  图数据立方体技术实质上就是将传统的数据立方体与多维网络进行结合。在图数据立方体中，上图的多维网络就是它的Base Cuboid。图数据立方体的示意图如下所示。

  在上图中，除了最下方的Base Cuboid，其余的方体称为聚合网络(Aggregation Network)。下图为聚合网络与传统方体的聚合表的对比。

(Gender)方体
(Gender, Location)方体

  可以看到图数据立方体的方体——聚合网络保存了个体之间的关系。图中顶点内的数字表示在Base Cuboid中对应的个体数；图中边上的数字表示在Base Cuboid中对应个体之间的边数。

Graph Cube的联机分析处理

  联机分析处理(OLAP)，是人们对数据仓库最主要的操作方式，在模型中就是根据要求计算出相应的方体，将结果方体以表格的形式展示给数据分析师。
  在图数据立方体中的OLAP分为两种形式：基于单个方体的查询(Cuboid Query)，基于多个方体的查询(Crossboid Query)。

基于单个方体的查询

  该查询形式与一般的数据仓库查询形式基本相同，系统根据用户给定的属性计算出图数据立方体中对应的方体，将聚合网络返回给用户。下图为图数据立方体中的各个方体。

  方体的聚合网络构建算法如下所示。

  算法通过哈希函数构造属性与顶点的关系。对于查询属性相同的个体，将被映射到相同的顶点。
  首先生成聚合网络的顶点。3-8行循环遍历Bsae Cuboid的多维网络中的所有顶点，即所有个体。若映射的顶点不存在，则创建新的顶点，并为顶点赋予权值1；若映射的顶点已存在，则为顶点的权值加1。
  接着生成聚合网络的边。9-15行循环遍历Bsae Cuboid的多维网络中的所有边，即个体间的关系。根据边的首尾顶点，找到对应聚合网络中的两个顶点。若两顶点间不存在边，则创建边，并为边赋予权值1；若已存在边，则为边的权值加1。
最后将生成的聚合网络返回给用户。

  如果聚合网络A已算出，用户希望获得另一个聚合网络B，并且B是A的祖先(即B的属性集是A的真子集)，此时可以直接通过聚合网络A计算出聚合网络B。将上述算法的输入网络由多维网络改成聚合网络A即可。

基于多个方体的查询

考虑如下问题。

ID=3的用户与不同地区的用户之间的关系网络是怎样的？

  可以看到，这种查询要求仅计算一个方体是不够的。

  在基于多个方体的查询形式下，用户需要的聚合网络横跨多个方体。作者在这里以2个方体为例进行分析，将2个方体的结合称为跨方体(Crossboid)。跨方体由2个方体通过连接操作构建而成。跨方体与方体的关系如下图所示。图中包含了三个方体和两个跨方体。

  两个跨方体的聚合网络分别如下图所示。

按性别分类的用户与按地区分类的用户之间的关系网络

ID=3的用户与不同地区的用户之间的关系网络

  我们知道，在维度为n的图数据立方体中有2ⁿ个方体。每个方体可以跟任意方体（包括本身，若是本身则连接后不变）进行连接组成一个跨方体，所有共有2ⁿ×2ⁿ=2²ⁿ个跨方体。

  计算跨方体聚合网络的算法如下所示。

  算法的大致思路与上一个算法相同，同样是构造哈希函数映射属性与顶点的关系，依次构造聚合网络的顶点和边。区别在于构造边的时候，该算法将多维网络中的无向边作为有向边考虑。

  与上一个算法类似，跨方体网络的计算也可以进行简化。若用户希望获得方体S与方体T连接的跨方体ST的聚合网络，系统可以直接通过S与T的最近共同子孙方体NCD(S,T)的网络计算。方法同样是将输入的多维网络改为NCD(S,T)的聚合网络。