1、加法器的概述
二进制的半加器(详情),也就是实现(0+0=00、1+0=01、0+1=01及1+1=10),一个与门可实现进位输出,一个异或门可实现加和位输出,这样就组成了一个半加器,两个半加器与一个或门组成一个全加器,多个全加器串联起来,可进行多位二进制数的运算,8位全加器串联就可计算255以内的加法,16位全加器串联就能计算65535以内的加法。
然后说今天的主角,只能说Dmitry V. Sokolov真是个天才,提出了最为基础的零件:三态多路复用器 (原文),并用这基础块实现了平衡三进制的全加器,更加牛的是硬件也搞出来了,并不是仅仅纸上谈兵而以。
PS:可以先看原文再看本文,本文只讲如何理解~~~
2、三态多路复用器(基础块)
这计算机中唯一使用的基础块是三态多路复用器。它用 CMOS 模拟开关来组成,有五个引脚,分别为:S、N、O、P、C;其中S为数据选择端,C为数据输出端,而(N、O、P)都为数据输入端;它的输入及输出都为三元信号,也就是-1(负电压)、0(零电压)、1(正电压),示意图如下:
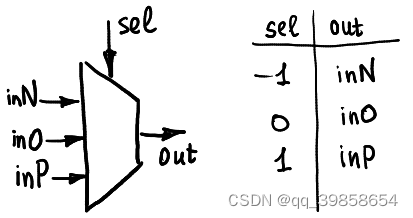
- 当S端输入为-1时,N端到Out形成双向通路,O端及P端与Out关闭;
- 当S端输入为 0时,O端到Out形成双向通路,N端及P端与Out关闭;
- 当S端输入为 1时,P端到Out形成双向通路,N端及O端与Out关闭;
基础硬件设计由Shaos所提出的,Dmitry V. Sokolov唯一做的就是创建 SMD 版本的 TRIMUX(简化硬件),硬件示意图:

2.1硬件的实现
表面贴装 dg403 开关,在找到这个设计之前,我尝试使用 cd4007 和 cd4016 的组合。确实有效,但硬件又笨重又丑陋。 DG403 交换机提供真正的三进制计算可能性,没有任何冗余,例如使用两位二进制并禁止四种配置之一。
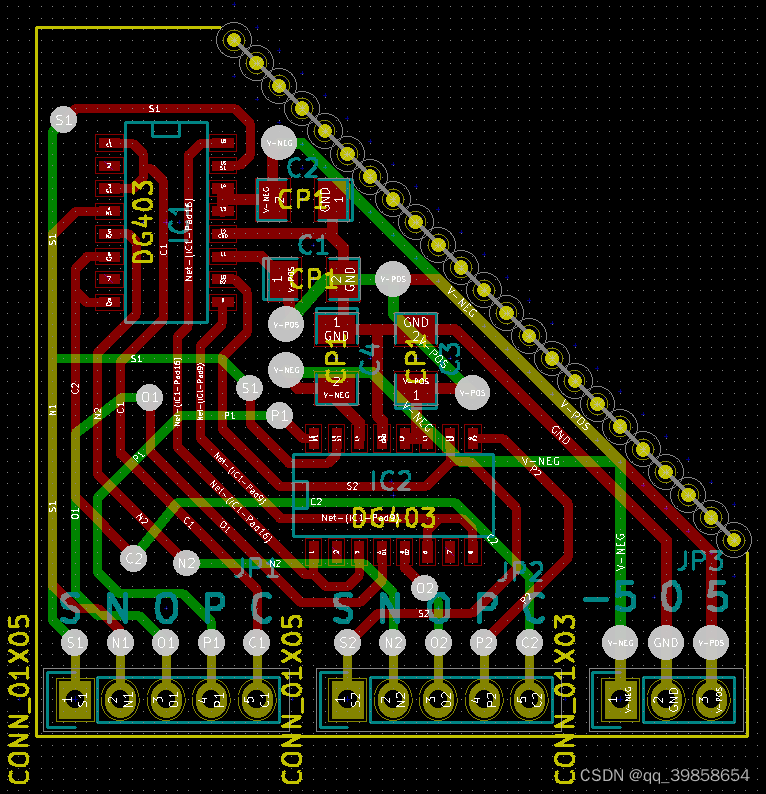
两个 DG403 可以组成一个三元多路复用器:其中一个 IC 接收 -5V 至 0V 电源输入,而另一个 IC 则由 0V 至 5V 供电,它允许使用分别由三个电压 -5V、0V 和 5V 表示的三元信号。此设计仅使用一半的 dg403 引脚,因此很自然地会创建一个带有两个多路复用器的电路板。
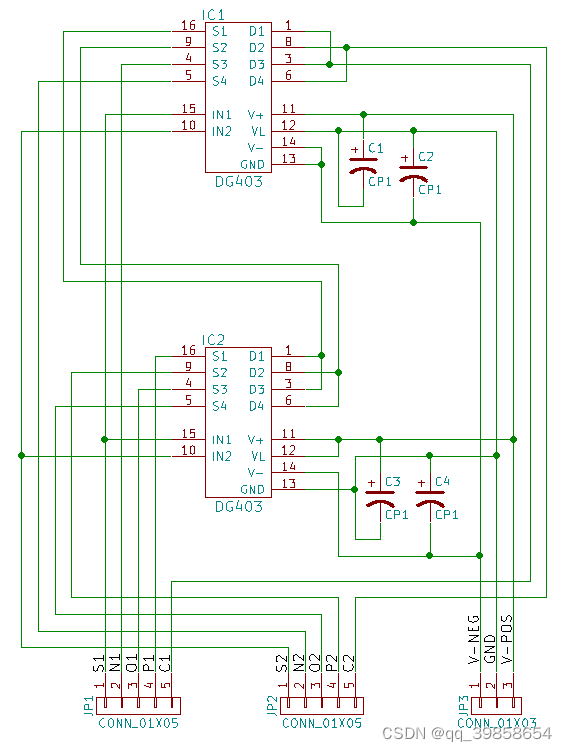
请随时联系这里的Shaos 。了不起的家伙,他没有猜测三态的好处,而是设计并制造了自己的三态 IC!

2.2硬件设计猜想
上文中文章用硬件,确实很巧妙,就像是电路就是只有开与关二种状态,可当引入负电源后就变对称了,双电源分为正电源及负电源就多了一种状态,那就是电流的流动方向之;二种状态就是单一方向的电流的通断,三种状态就是逆时针的电流、断开的无电流、顺时针的电流;它的硬件也是高度对称,要想处理-5v到+5v电压很麻烦,但处理(-5v至0v)及(0v到+5v)就变得清晰明了,讲究的就是一个对称性。
三元多路复用器,就是一个单刀三掷开关,若能设计一个专用的硬件,那体积将能做的更小,这元件分为三层:上层、中间层、下层,元件可以根据输入电压快速切换层级,以下为工作原理:
- 当两端施没有电压时,中间层默认导通,也只有中间层有导电的电子;
- 当两端施加负电压时,形成向上电场,导电的电子到达上层,上层导通中间层截断,然后断电利用电容放电,电子又自动回到中间层;
- 当两端施加正电压时,形成向下电场,导电的电子到达下层,下层导通中间层截断,然后断电利用电容放电电子又自动回到中间层;
前苏联的三进制计算机,有一个基础的元件,能够充当受控电流互感器;它由Brusentsov工程师设计的,采用两个铁氧体磁芯及半导体二极管组合而成,每天早上,他们从铁氧体磁芯开始,使用普通缝纫针在其上缠绕 52 圈电线。然后将核心交给技术人员,通过组合两个铁氧体元件,可以表示三种稳定状态的方式接线,技术人员完成组装过程并将其安装到块上,这种方法很成功,但没有减少所需元件的数量。因为实际上,这两个铁氧体磁芯可能代表两个二进制位,这2^2比一个三元“trit”( ) 代表更多的信息 ( 3^1)。唉,至少他们的功耗减少了。
所以说,即使苏联老大哥那么强的工业基础,也是要两个铁氧体磁芯才能搞定三种状态,因为铁氧体磁芯有且只有两种状态,自然界中三稳态东西太少了,当一个搞不定时就再引入一个,对的,讲究的还是一个对称性,就像正负电压(详情)一样,当所以不可能都排除后,剩下的就是真正的答案。
3、平衡三进制输入(一元函数)
现在,用多路复用器将 -1、0 和 1分别赋予不同的输入引脚,从而得到不同的一元函数。分别计算(A+1)与(A-1)的值,从而得输入信号:
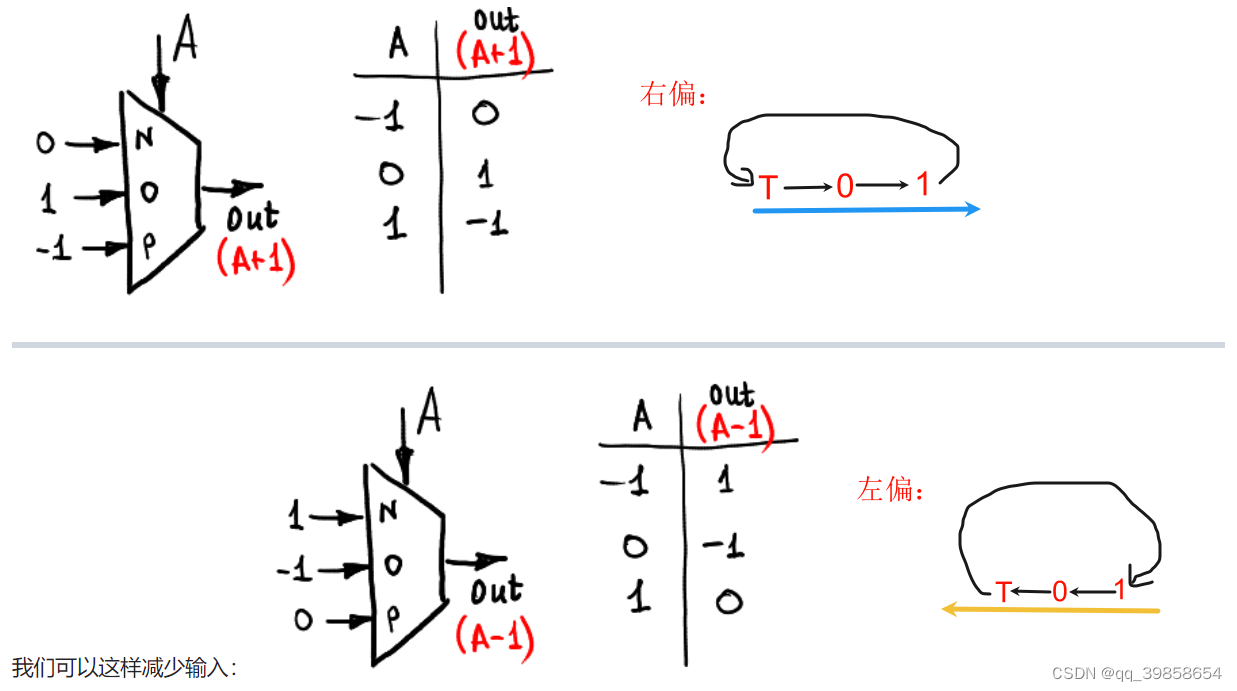
如下图所示,分别为min(A,0)和max(A,0)
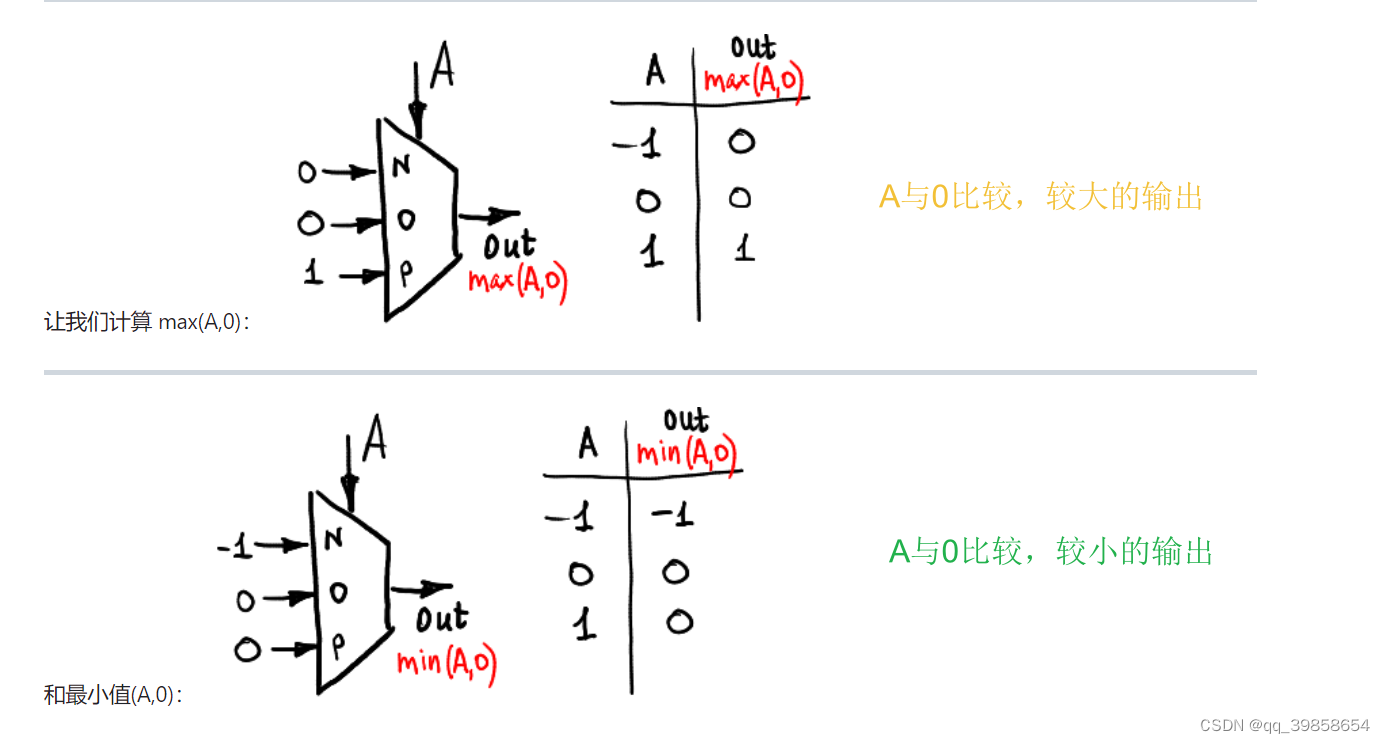
上述的图怎么理解,可以说它是简化了输入,有点编码的意思了,就像是莫尔斯电码,短点称“嘀”,长一些的称“哒”,一组特定的“嘀”、“哒”组合表示一种信息,所以上述也是一样的,它的电压顺序可不是随便编的,让我们重新回到平衡三进制的加法表,如下图所示:
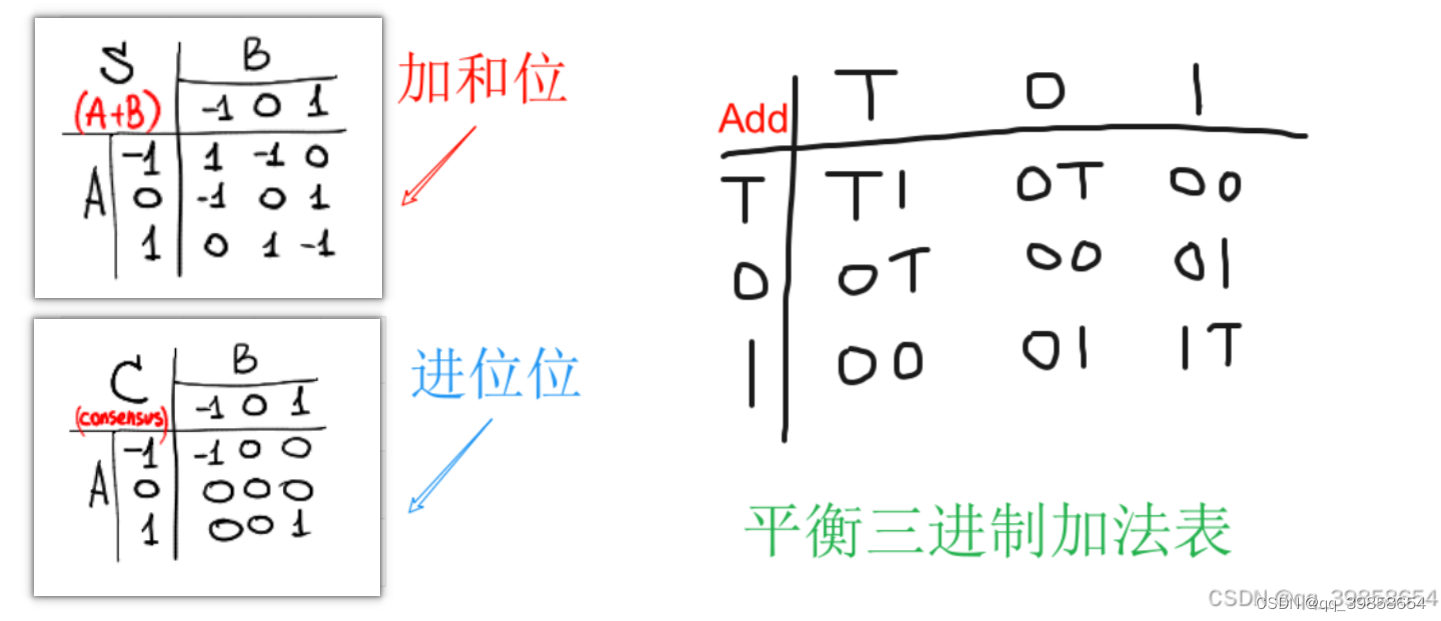
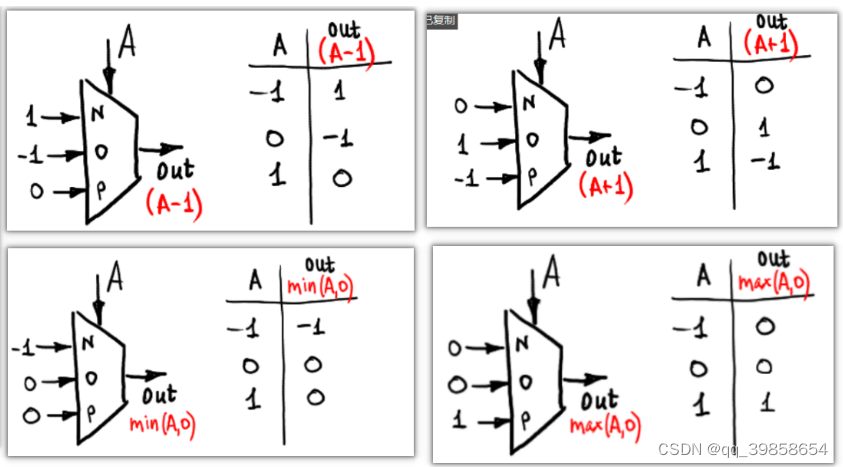
看上面的两张图,有联系了吧!加和位表中按列来分,值分别为(A-1)、A、(A+1),也就是用三个基础块可以实现加和位表;进位位表中按列来分,值分别为min(A,0)、0、max(A,0),用三个基础块可实现进位位表;也就是说,它提前把值给写好了,这线路是连接死的,先是A输入产生数据,然后B按规则依次输出即可。
4、平衡三进制半加器(两参数函数)
一个多路复用器允许我们计算任何一元函数,当有两层多路复用器,就可以先让第一层计算 A 的一元函数,第二层根据 B 将它们组合起来,这样就可以分别实现进位表与加和表,最终形成一个加法器。
4.1半加器的模型
4.1.1加和位的实现(Sum)
当我们想要计算两个信号 A 和 B的和,那么我们可以使用以下形式:
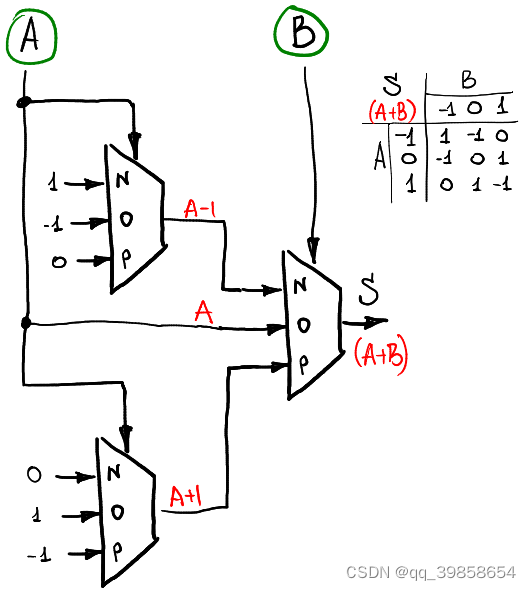

4.1.2进位的实现(Consensus)
如果我们想计算两个三元信号的共识函数(如果 A=B=-1,则共识等于 -1,如果 A=B=1,则共识等于 1,否则为零),那么我们可以这样做:
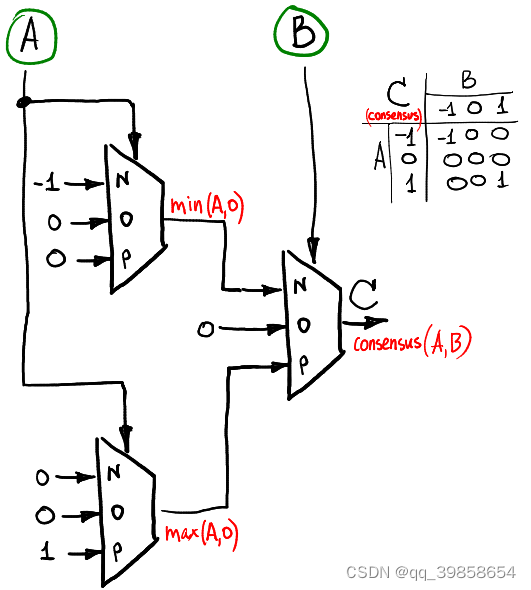

4.2半加器的实现
4.2.1半加器软件模拟实现
使用二个字符来作为它的一个数据,得代码如下:
#include <iostream>
#include <vector>
using namespace std;
// 左偏
char toTargetLeftChar(char c) {
switch (c) {
case '0': return 'T';
case '1': return '0';
case 'T': return '1';
default: return '\0';
}
}
// 右偏
char toTargetRightChar(char c) {
switch (c) {
case '1': return 'T';
case 'T': return '0';
case '0': return '1';
default: return '\0';
}
}
//最小值
char toTargetMinChar(char c){
switch (c) {
case 'T': return 'T';
case '0':
case '1': return '0';
default: return '\0';
}
}
//最大值
char toTargetMaxChar(char c){
switch (c) {
case '1': return '1';
case '0':
case 'T': return '0';
default: return '\0';
}
}
char AdderPos(char a,char b){
char lastResult='\0';
switch (b) {
case 'T':
lastResult=toTargetLeftChar(a);
break;
case '0':
lastResult=a;
break;
case '1':
lastResult=toTargetRightChar(a);
break;
}
return lastResult;
}
char CoutPos(char a,char b){
char lastResult='\0';
switch (b) {
case 'T':
lastResult=toTargetMinChar(a);
break;
case '0':
lastResult='0';
break;
case '1':
lastResult=toTargetMaxChar(a);
break;
}
return lastResult;
}
// 定义一个函数来输出二维 vector
void print2DVector(const vector<char>& vec,const vector<char>& vec2) {
char inA='\0';
char inB='\0';
for(int i=0;i<vec.size();i++){
for(int j=0;j<vec2.size();j++){
inA=vec[i];
inB=vec2[j];
cout<<inA<<"+"<<inB<<"=";
cout<<CoutPos(inA,inB)<<AdderPos(inA,inB)<<";"<<endl;
}
cout<<endl;
}
}
int main()
{
vector<char> c1={'T','0','1'};
vector<char> c2={'T','0','1'};
print2DVector(c1,c2);
return 0;
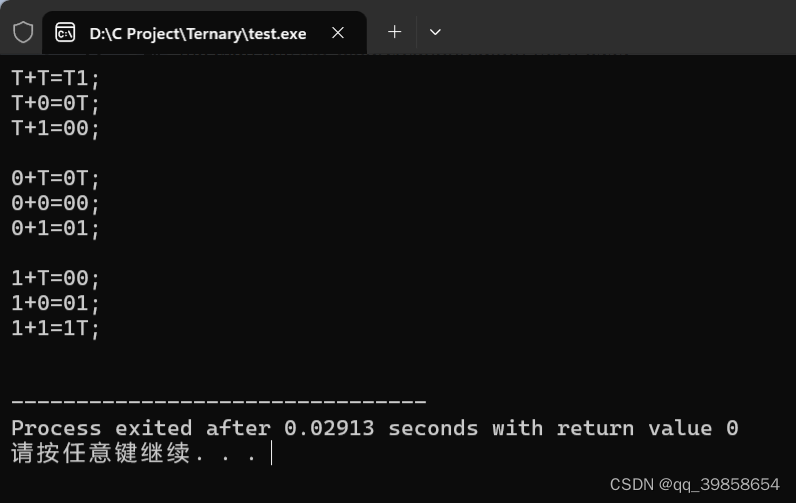
}得出结果如下:
4.2.2半加器的硬件实现
让我们测试一下设计吧! 下图为一个半加器,其红色 LED 表示 -1,关闭表示 0,绿色 LED 表示 1,输入A和B两个值,得到 S(和) 和 C(进位) 两个输出。因此,这张照片告诉我们 S=-1,C=1,或者换句话说,1+1 = (3^1) * 1 + (3^0) * -1:

5、平衡三进制全加器(三参数函数)
二进制的全加器,用2个半加器及1个或门组成的,全加器最大的特点就是可以串联起来,从而实现多位的加法运算,全加器有三个输入: A、B、Cin,有两个输出 S 和 Cout。本质上也就是三个值相加,先是A与B相加,然后(A+B)的值再与Cin相加。当为二进制数时,即有2^3=8种结果,当为平衡三进制时,则有3^3=27种结果,如下图所示:

想要计算 A+B+Cin 的和,可以先列出27种结果,它的值非常对称,当Cin=0时,那它的值跟之前讲的半加器输出一样,所以以Cin表为中间表,分别列出Cin=-1及Cin=1时的三个表,如下图所示: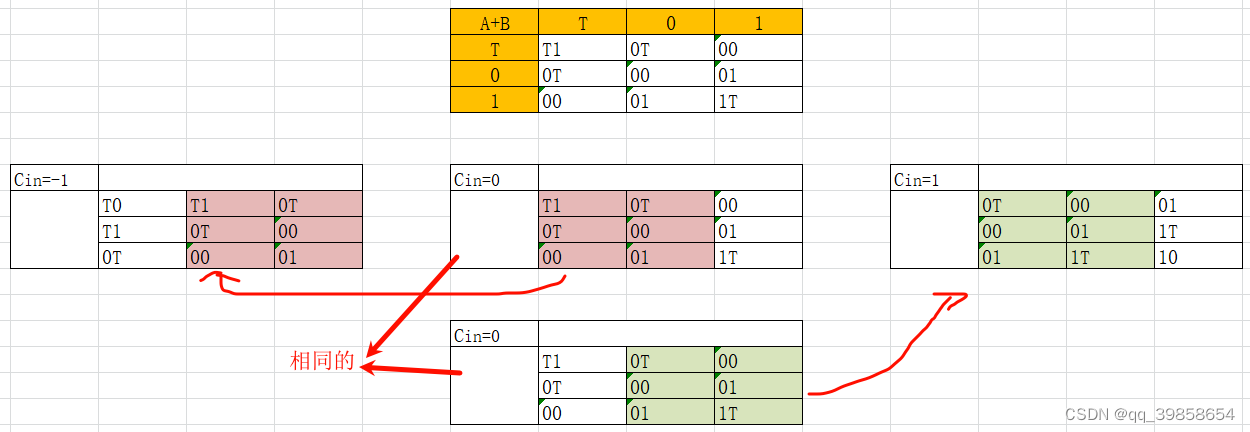
注意看上图,以最上面的半加器表为基础,然后Cin=0得到一张一样的表,然后再今Cin=-1及Cin=1得到另外俩张表,这样27种结果,观察一下,Cin=0表对Cin=-1、Cin=1都有重合部分,然后就好办了,于是将三张表合并得到:
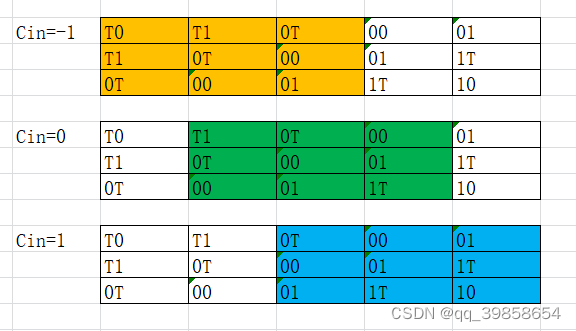
这个又有什么用呢?三张表都一样,只要其中一张就可以表示所有的输出结果了,这样将它的加法位与进位位分开,就得了它的输入逻辑了,如下图所示:
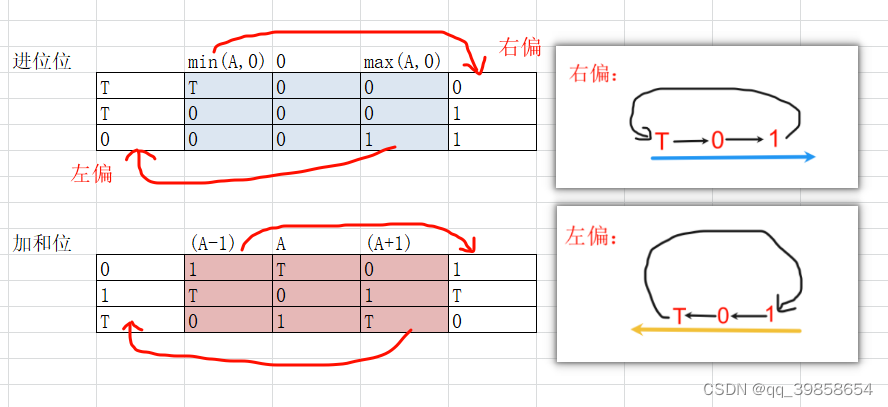
最后根据上述的推理过程,就可以完成全加器的所有设计了,推出的设计跟Dmitry V. Sokolov本人的一样,如果能设计出左偏、右偏元件那就更好了,设计思路如下图所示:
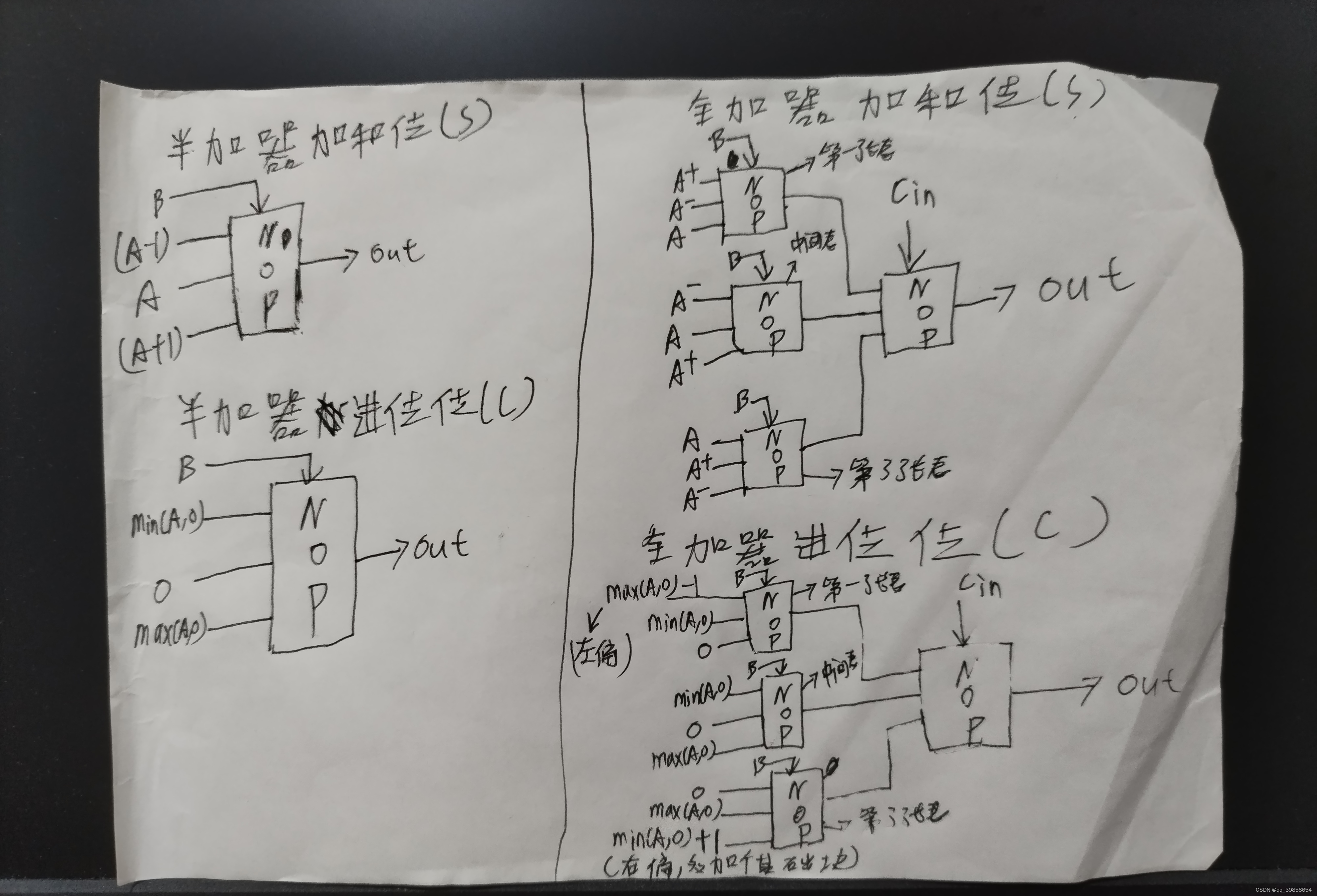
5.1全加器的模型
5.1.1加和位的实现(三数之和)
与之前想法相同,使用逐层准备输入。第一层接收 A 作为输入,第二层使用 B筛选,最后一层使用 Cin选择输出:
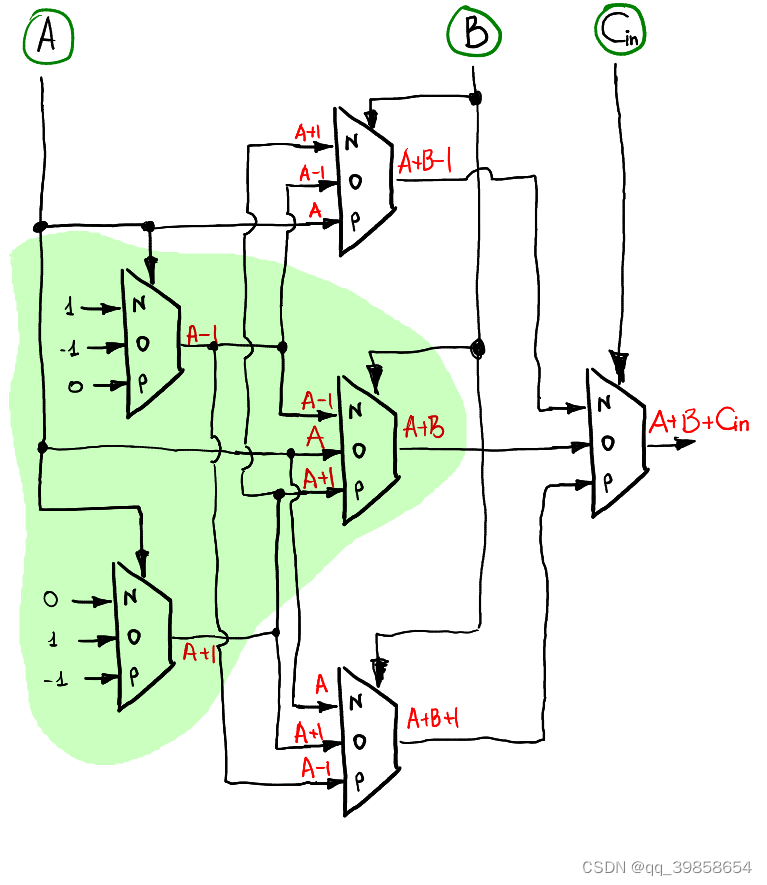
5.1.2进位位的实现(三数之进)
相同的思路,三个数相加后的进位,用逐层方式来计算,
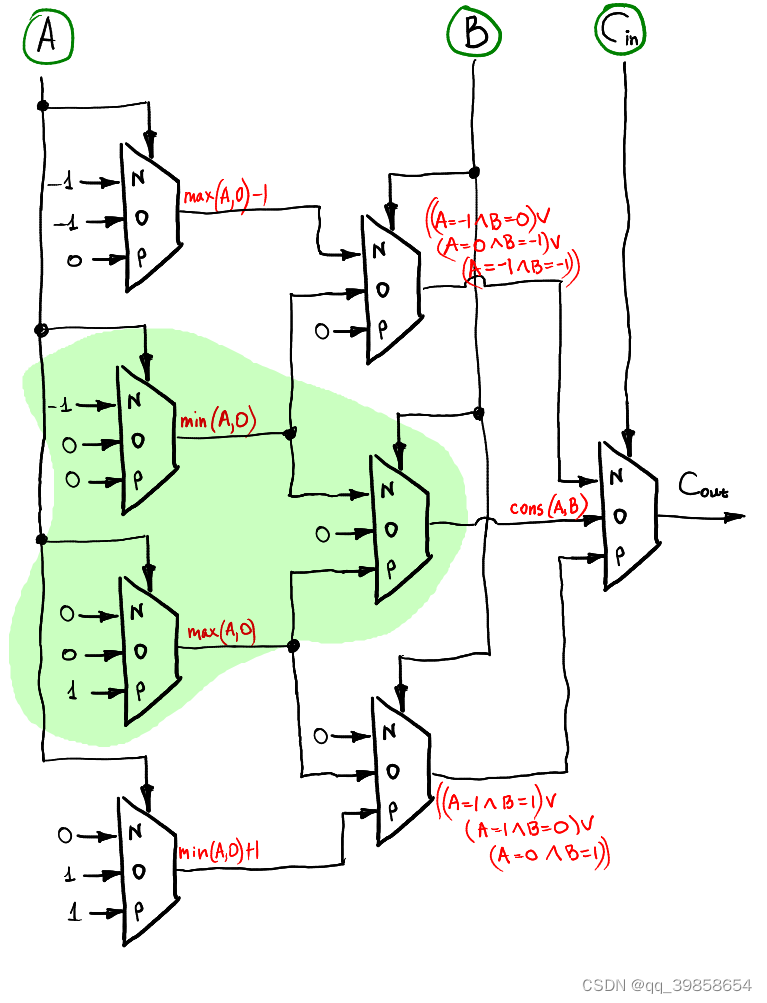
5.2全加器的实现
5.2.1全加器软件模拟实现
使用三个字符来作为它的一个数据,得代码如下:
#include <iostream>
#include <vector>
using namespace std;
// 左偏(A-1)
char toTargetLeftChar(char c) {
switch (c) {
case '0': return 'T';
case '1': return '0';
case 'T': return '1';
default: return '\0';
}
}
// 右偏(A+1)
char toTargetRightChar(char c) {
switch (c) {
case '1': return 'T';
case 'T': return '0';
case '0': return '1';
default: return '\0';
}
}
//最小值Min(A,0)
char toTargetMinChar(char c){
switch (c) {
case 'T': return 'T';
case '0':
case '1': return '0';
default: return '\0';
}
}
//最大值Max(A,0)
char toTargetMaxChar(char c){
switch (c) {
case '1': return '1';
case '0':
case 'T': return '0';
default: return '\0';
}
}
char AdderPos(char a,char b){
char lastResult='\0';
switch (b) {
case 'T':
lastResult=toTargetLeftChar(a);
break;
case '0':
lastResult=a;
break;
case '1':
lastResult=toTargetRightChar(a);
break;
}
return lastResult;
}
char CoutPos(char a,char b){
char lastResult='\0';
switch (b) {
case 'T':
lastResult=toTargetMinChar(a);
break;
case '0':
lastResult='0';
break;
case '1':
lastResult=toTargetMaxChar(a);
break;
}
return lastResult;
}
char AdderPos(char a,char b,char c){
char lastResult='\0';
char leftResult=toTargetLeftChar(a);
char rightResult=toTargetRightChar(a);
switch (b) {
case 'T':
if(c=='T'){
lastResult=rightResult;
}else if(c=='0'){
lastResult=leftResult;
}else if(c=='1'){
lastResult=a;
}
break;
case '0':
if(c=='T'){
lastResult=leftResult;
}else if(c=='0'){
lastResult=a;
}else if(c=='1'){
lastResult=rightResult;
}
break;
case '1':
if(c=='T'){
lastResult=a;
}else if(c=='0'){
lastResult=rightResult;
}else if(c=='1'){
lastResult=leftResult;
}
break;
}
return lastResult;
}
char CoutPos(char a,char b,char c){
char lastResult='\0';
char minReuslt=toTargetMinChar(a);
char maxReuslt=toTargetMaxChar(a);
switch (b) {
case 'T':
if(c=='T'){
lastResult=toTargetLeftChar(maxReuslt);
}else if(c=='0'){
lastResult=minReuslt;
}else if(c=='1'){
lastResult='0';
}
break;
case '0':
if(c=='T'){
lastResult=minReuslt;
}else if(c=='0'){
lastResult='0';
}else if(c=='1'){
lastResult=maxReuslt;
}
break;
case '1':
if(c=='T'){
lastResult='0';
}else if(c=='0'){
lastResult=maxReuslt;
}else if(c=='1'){
lastResult=toTargetRightChar(minReuslt);
}
break;
}
return lastResult;
}
// 定义一个函数来输出二维 vector
void print2DVector(const vector<char>& vec,const vector<char>& vec2,char Cin) {
char inA='\0';
char inB='\0';
for(int i=0;i<vec.size();i++){
for(int j=0;j<vec2.size();j++){
inA=vec[i];
inB=vec2[j];
// cout<<inA<<inB<<":"<<Cin;
cout<<CoutPos(inA,inB,Cin)<<AdderPos(inA,inB,Cin)<<" ";
}
cout<<endl;
}
}
int main()
{
vector<char> c1={'T','0','1'};
vector<char> c2={'T','0','1'};
char Cin='T';
print2DVector(c1,c2,Cin);
return 0;
}5.2.2全加器的硬件实现
Dmitry V. Sokolov懒得用面包板来测试全加器,所以做了个单层PCB板:

铜被蚀刻后的样子:

下面是它如何求解 -4 + 2(最不重要的 trit 位于左侧):

当然,我们不需要用于最低有效 trit 的全加器板(我们没有用于最低有效 trit 的输入的进位标志),半加器就足够了。
结尾:至此,我们可以说已经完成了基础的运算设计,若要需要更复杂的运算则需要以此为基础继续进行延伸发展。
参考资料:
1、Ternary computing: basics · ssloy/tutorials Wiki · GitHub
2、The Balanced Ternary Machines of Soviet Russia - DEV Community
3、https://hackmd.io/@jx-9TgcOR064N3oN7__dvg/H1N168fsZ?type=view






















 3919
3919

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








