应用统计期末复习
1. Matlab 矩阵寻访,剪裁,拼接
A = [1 2; 3 4]

- 取第二行
A(2, :)

- 取第二列
A(:, 2)

- 将第二行第二列元素赋值为 5
A(2, 2) = 5

- 右边拼接 2 行 1 列的全一矩阵
[A, ones(2, 1)]

- 下面拼接 2 行 2 列的全零矩阵
[A; zeros(2, 2)]or[A; zeros(2)]

- 删除第 2 列元素
A(:, 2) = []

2. 常见概率密度分布
2.1 常见函数类型名称
- 概率密度函数
pdf - 累积分布函数
cdf - 逆累积分布函数
inv
求随机变量 X X X 在 x x x 点处的分布函数的反函数值 x = F − 1 ( y ) x = F^{-1}(y) x=F−1(y) - 均值与方差计算函数
stat - 随机数生成函数
rnd
2.2 常见分布类型名称
- 正态分布
norm
f ( x ) = 1 2 π δ e − ( x − μ ) 2 2 δ 2 E ( X ) = μ D ( X ) = δ 2 f(x) = \frac{1}{\sqrt{2\pi}\delta}e^{-\frac{(x-\mu)^2}{2\delta^2}} \\ E(X) = \mu \\ D(X) = \delta^2 f(x)=2πδ1e−2δ2(x−μ)2E(X)=μD(X)=δ2 - 指数分布
exp
f ( x ) = { 1 θ e − x θ , x > 0 0 , else F ( X ) = { 1 − e − x θ , x > 0 0 , else E ( X ) = θ D ( X ) = θ 2 f(x)= \begin{cases}\frac{1}{\theta} e^{-\frac{x}{\theta}}, & x>0 \\ 0, & \text {else}\end{cases} \\ F(X)= \begin{cases}1-e^{-\frac{x}{\theta}}, & x>0 \\ 0, & \text {else}\end{cases} \\ E(X)=\theta \\ D(X)=\theta^{2} \\ f(x)={θ1e−θx,0,x>0elseF(X)={1−e−θx,0,x>0elseE(X)=θD(X)=θ2
推导:https://blog.csdn.net/saltriver/article/details/53982885 - 均匀分布
unif
f ( x ) = { 1 b − a , a < x < b 0 , else F ( X ) = { 0 , x < a x − a b − a , a ≤ x < b 1 , x ≥ b E ( X ) = a + b 2 D ( X ) = ( b − a ) 2 12 f(x)= \begin{cases}\frac{1}{b-a}, & a<x<b \\ 0, & \text { else }\end{cases} \\ F(X)= \begin{cases}0, & x<a \\ \frac{x-a}{b-a}, & a \leq x<b \\ 1, & x \geq b\end{cases} \\ E(X) = \frac{a + b}{2} \\ D(X) = \frac{(b - a)^2}{12} f(x)={b−a1,0,a<x<b else F(X)=⎩⎪⎨⎪⎧0,b−ax−a,1,x<aa≤x<bx≥bE(X)=2a+bD(X)=12(b−a)2 - 二项分布
bino
P ( X = k ) = C n k p k ( 1 − p ) n − k P(X=k)=C_{n}^{k} p^{k}(1-p)^{n-k} P(X=k)=Cnkpk(1−p)n−k
E ( X ) = n p E(X) = np E(X)=np
D ( X ) = n p ( 1 − p ) D(X) = np(1-p) D(X)=np(1−p)
推导:https://blog.csdn.net/s20091103372/article/details/39716761 - 泊松分布
poiss
f ( X = k ) = λ k k ! e − λ F ( X ≤ x ) = ∑ k = 0 x λ k k ! e − λ E ( X ) = D ( X ) = λ f(X=k) = \frac{\lambda^k}{k!}e^{-\lambda} \\ F(X \le x) = \sum_{k=0}^{x} \frac{\lambda^k}{k!}e^{-\lambda} \\ E(X) = D(X) = \lambda f(X=k)=k!λke−λF(X≤x)=k=0∑xk!λke−λE(X)=D(X)=λ
推导:https://blog.csdn.net/saltriver/article/details/52969014
2.3 Matlab 具体函数命名规则
函数名 = 分布类型名称 + 函数类型名称 (除了poisstat)
-
poisspdf(5, 2)表示随机变量服从 λ = 2 \lambda = 2 λ=2 的泊松分布在 x = 5 的概率密度值 p = P(x=5)
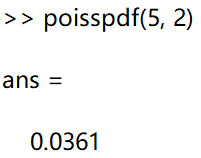
-
normcdf(0.5, 0, 1)表示随机变量服从 μ = 0 , σ = 1 \mu = 0, \sigma = 1 μ=0,σ=1 的正态分布,在 x = 0.5 处的分布函数值 y = F(x = 0.5)

-
[m, v] = normstat(0, 5)给出正态分布 μ = 0 , σ = 5 \mu = 0, \sigma = 5 μ=0,σ=5,求其均值 m 和方差 v

2.3.1 α \alpha α 分位数
- 计算标准正态分布的
0.05
0.05
0.05 分位数,下侧
α
\alpha
α 分位数
norminv(0.05, 0, 1)

- 计算标准正态分布的
0.05
0.05
0.05 分位数, 上侧
α
\alpha
α 分位数
norminv(0.95, 0, 1)

- 计算标准正态分布的
0.05
0.05
0.05 分位数, 双侧
α
/
2
\alpha/2
α/2 分位数
norminv(0.025, 0, 1)

norminv(0.975, 0, 1)

2.3.2 练习
-
计算参数为 2 的指数分布在 1 处的密度函数值,累积分布函数值;
p = exppdf(1, 2) % 概率密度函数
y = expcdf(1, 2) % 累积分布函数

-
计算参数为 30,0.3 的二项分布在 9 处的累积分布函数值;
y = binocdf(9, 30, 0.3)

-
计算参数为 3 的泊松分布在 0.5 处的逆累积分布函数值;
x = poissinv(0.5, 3)

-
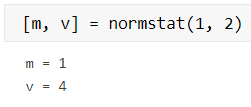
计算参数为 1,2 的正态分布的数学期望和方差;
[m, v] = normstat(1, 2)
-
模拟生成参数为 2,4 的正态分布随机数 2 行 6 列;
A = normrnd(2, 4, [2, 6])
2.4 抽样分布
2.4.1 χ 2 \chi^2 χ2 卡方分布
假设
X
1
,
X
2
,
.
.
.
,
X
n
X_1, X_2, ... ,X_n
X1,X2,...,Xn 是 n 个相互独立的标准正态分布
N
(
0
,
1
)
N(0, 1)
N(0,1) 随机变量,则
χ
2
=
∑
i
=
1
n
X
i
2
∼
χ
2
(
n
)
\chi^2 = \sum^{n}_{i=1}{X_i^2} \sim \chi^2(n)
χ2=i=1∑nXi2∼χ2(n)
χ
2
\chi^2
χ2 叫做自由度为 n 的卡方分布
2.4.2 t 分布
假设
X
∼
N
(
0
,
1
)
,
Y
∼
χ
2
(
n
)
X \sim N(0, 1), Y \sim \chi^2(n)
X∼N(0,1),Y∼χ2(n),且 X 和 Y 相互独立,则
t
=
X
Y
n
∼
t
(
n
)
t = \frac{X}{\sqrt{\frac{Y}{n}}} \sim t(n)
t=nYX∼t(n)
t 叫做自由度为 n 的 t 分布
2.4.3 F 分布
假设
X
∼
χ
2
(
n
1
)
,
Y
∼
χ
2
(
n
2
)
X \sim \chi^2(n_1), Y \sim \chi^2(n_2)
X∼χ2(n1),Y∼χ2(n2),且 X 与 Y 相互独立,则
F
=
X
/
n
1
Y
/
n
2
∼
F
(
n
1
,
n
2
)
F = \frac{X/n_1}{Y/n_2} \sim F(n_1, n_2)
F=Y/n2X/n1∼F(n1,n2)
F 叫做自由度为
n
1
,
n
2
n_1, n_2
n1,n2 的 F 分布,其中
n
1
,
n
2
n_1, n_2
n1,n2 分别叫做第一自由度和第二自由度。
F 分布有以下重要性质:
倒数对称性
F
1
−
α
(
n
1
,
n
2
)
=
1
F
α
(
n
2
,
n
1
)
F_{1-\alpha}(n_1, n_2) = \frac{1}{F_{\alpha}(n_2, n_1)}
F1−α(n1,n2)=Fα(n2,n1)1
2.4.4 U 分布(样本均值分布)
设
X
1
,
X
2
,
.
.
.
,
X
n
X_1, X_2, ..., X_n
X1,X2,...,Xn 是来自总体
N
(
μ
,
δ
2
)
N(\mu, \delta^2)
N(μ,δ2) 的样本,则
X
ˉ
=
1
n
∑
i
=
1
n
X
i
∼
N
(
μ
,
δ
2
n
)
U
=
X
ˉ
−
μ
δ
/
n
∼
N
(
0
,
1
)
\bar{X} = \frac{1}{n}\sum^{n}_{i=1}{X_i} \sim N(\mu, \frac{\delta^2}{n}) \\ U = \frac{\bar{X} - \mu}{\delta / \sqrt{n}} \sim N(0, 1)
Xˉ=n1i=1∑nXi∼N(μ,nδ2)U=δ/nXˉ−μ∼N(0,1)
2.5 补充
2.5.1 若 X ∼ N ( 0 , 1 ) X \sim N(0, 1) X∼N(0,1), 则 X 2 ∼ χ 2 ( 1 ) X^2 \sim \chi^2(1) X2∼χ2(1)
2.5.2 若 X ∼ t ( n ) X \sim t(n) X∼t(n),则 X 2 ∼ F ( 1 , n ) X^2 \sim F(1, n) X2∼F(1,n)
证明:
若
X
∼
t
(
n
)
X \sim t(n)
X∼t(n),则存在
Y
∼
N
(
0
,
1
)
,
Z
∼
χ
2
(
n
)
Y \sim N(0, 1), Z \sim \chi^2(n)
Y∼N(0,1),Z∼χ2(n),Y 和 Z 相互独立,使得
X
=
Y
Z
/
n
X = \frac{Y}{\sqrt{Z/n}}
X=Z/nY
又因为
Y
2
∼
χ
2
(
1
)
Y^2 \sim \chi^2(1)
Y2∼χ2(1),则
X
2
=
Y
2
Z
/
n
=
Y
2
/
1
Z
/
n
∼
F
(
1
,
n
)
X^2 = \frac{Y^2}{Z/n} = \frac{Y^2/1}{Z/n} \sim F(1, n)
X2=Z/nY2=Z/nY2/1∼F(1,n)
2.5.3 例题
例:
X
1
,
X
2
,
.
.
.
,
X
9
X_1, X_2, ... , X_9
X1,X2,...,X9 是来自
X
∼
N
(
0
,
2
2
)
X \sim N(0, 2^2)
X∼N(0,22) 的简单随机样本,求系数
a
,
b
,
c
a, b, c
a,b,c 使得
Y
=
a
(
X
1
+
X
2
)
2
+
b
(
X
3
+
X
4
+
X
5
)
2
+
c
(
X
6
+
X
7
+
X
8
+
X
9
)
2
Y = a(X_1 + X_2)^2 + b(X_3 + X_4 + X_5)^2 + c(X_6 + X_7 + X_8 + X_9)^2
Y=a(X1+X2)2+b(X3+X4+X5)2+c(X6+X7+X8+X9)2
Y 服从卡方分布,并求其自由度。
证明:
由
X
∼
N
(
0
,
4
)
X \sim N(0, 4)
X∼N(0,4),
可得
E
(
X
1
+
X
2
)
=
E
(
X
1
)
+
E
(
X
2
)
=
0
E(X_1 + X_2) = E(X_1) + E(X_2) = 0
E(X1+X2)=E(X1)+E(X2)=0 ,
D
(
X
1
+
X
2
)
=
D
(
X
1
)
+
D
(
X
2
)
=
8
D(X_1 + X_2) = D(X_1) + D(X_2) = 8
D(X1+X2)=D(X1)+D(X2)=8,
所以
X
1
+
X
2
∼
N
(
0
,
8
)
X_1 + X_2 \sim N(0, 8)
X1+X2∼N(0,8)
标准化可得
X
1
+
X
2
−
0
−
0
8
∼
N
(
0
,
1
)
\frac{X_1 + X_2 - 0 - 0}{\sqrt{8}} \sim N(0, 1)
8X1+X2−0−0∼N(0,1)
所以由卡方分布定义可得
(
X
1
+
X
2
)
2
8
∼
χ
2
(
1
)
⇒
a
=
1
8
\frac{(X_1 + X_2)^2}{8} \sim \chi^2(1) \Rightarrow a = \frac{1}{8}
8(X1+X2)2∼χ2(1)⇒a=81
同理可得
b
=
1
12
,
c
=
1
16
b = \frac{1}{12}, c = \frac{1}{16}
b=121,c=161
3. 统计估计
3.1 点估计-极大似然估计
求极大似然估计(MLE)的步骤为:
(1)由总体的概率密度写出似然函数
L
(
θ
)
=
L
(
x
1
,
x
2
,
.
.
.
,
x
n
;
θ
)
=
∏
i
=
1
n
p
(
x
i
;
θ
)
L(\theta) = L(x_1, x_2, ... , x_n; \theta) = \prod^{n}_{i=1}{p(x_i; \theta)}
L(θ)=L(x1,x2,...,xn;θ)=i=1∏np(xi;θ)
(2)求出对数似然函数
l
n
L
(
θ
)
lnL(\theta)
lnL(θ)
(3)求解方程得到
θ
^
\hat{\theta}
θ^
d
l
n
L
(
θ
)
d
θ
=
0
\frac{dlnL(\theta)}{d\theta} = 0
dθdlnL(θ)=0
3.2 区间估计
3.2.1 两个总体均值差 μ 1 − μ 2 \mu_1 - \mu_2 μ1−μ2 的置信区间
3.2.1.1 方差 δ 1 2 , δ 2 2 \delta_1^2, \delta_2^2 δ12,δ22 已知时 (U 分布)
X
ˉ
−
Y
ˉ
∼
N
(
μ
1
−
μ
2
,
δ
1
2
n
1
+
δ
2
2
n
2
)
\bar{X} - \bar{Y} \sim N(\mu_1 - \mu_2, \frac{\delta^2_1}{n_1} + \frac{\delta^2_2}{n_2})
Xˉ−Yˉ∼N(μ1−μ2,n1δ12+n2δ22)
取枢轴量
U
=
(
X
ˉ
−
Y
ˉ
)
−
(
μ
1
−
μ
2
)
δ
1
2
n
1
+
δ
2
2
n
2
∼
N
(
0
,
1
)
U = \frac{(\bar{X} - \bar{Y}) - (\mu_1 - \mu_2)}{\sqrt{\frac{\delta^2_1}{n_1} + \frac{\delta^2_2}{n_2}}} \sim N(0, 1)
U=n1δ12+n2δ22(Xˉ−Yˉ)−(μ1−μ2)∼N(0,1)
μ
1
−
μ
2
\mu_1 - \mu_2
μ1−μ2 的
1
−
α
1 - \alpha
1−α 的置信区间(比如说置信度为 95%,也就是说
1
−
α
1 - \alpha
1−α 为 0.95 )为
(
X
ˉ
−
Y
ˉ
−
U
α
2
δ
1
2
n
1
+
δ
2
2
n
2
,
X
ˉ
−
Y
ˉ
+
U
α
2
δ
1
2
n
1
+
δ
2
2
n
2
)
(\bar{X} - \bar{Y} - U_{\frac{\alpha}{2}}\sqrt{\frac{\delta^2_1}{n_1} + \frac{\delta^2_2}{n_2}}, \bar{X} - \bar{Y} + U_{\frac{\alpha}{2}}\sqrt{\frac{\delta^2_1}{n_1} + \frac{\delta^2_2}{n_2}})
(Xˉ−Yˉ−U2αn1δ12+n2δ22,Xˉ−Yˉ+U2αn1δ12+n2δ22)
3.2.1.2 方差 δ 1 2 = δ 2 2 = δ 2 \delta_1^2 = \delta_2^2 = \delta^2 δ12=δ22=δ2 未知但相等 (t 分布)
μ
1
−
μ
2
\mu_1 - \mu_2
μ1−μ2 的
1
−
α
1 - \alpha
1−α 的置信区间为
(
X
ˉ
−
Y
ˉ
−
t
α
2
(
n
1
+
n
2
−
2
)
∙
S
w
1
n
1
+
1
n
2
,
X
ˉ
−
Y
ˉ
+
t
α
2
(
n
1
+
n
2
−
2
)
∙
S
w
1
n
1
+
1
n
2
)
(\bar{X} - \bar{Y} - t_{\frac{\alpha}{2}}(n_1 + n_2 - 2)\bullet S_w\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}, \bar{X} - \bar{Y} + t_{\frac{\alpha}{2}}(n_1 + n_2 - 2)\bullet S_w\sqrt{\frac{1}{n_1} + \frac{1}{n_2}})
(Xˉ−Yˉ−t2α(n1+n2−2)∙Swn11+n21,Xˉ−Yˉ+t2α(n1+n2−2)∙Swn11+n21)
其中
S
w
S_w
Sw 为
(
n
1
−
1
)
S
1
2
+
(
n
2
−
1
)
S
2
2
n
1
+
n
2
−
2
\sqrt{\frac{(n_1 - 1)S_1^2 + (n_2 - 1)S_2^2}{n_1 + n_2 - 2}}
n1+n2−2(n1−1)S12+(n2−1)S22
S
1
2
,
S
2
2
S_1^2, S_2^2
S12,S22 分别为两个样本的样本方差。
3.2.2 两个总体方差比 δ 1 2 δ 2 2 \frac{\delta_1^2}{\delta_2^2} δ22δ12 的置信区间 (F 分布)
δ
1
2
δ
2
2
\frac{\delta_1^2}{\delta_2^2}
δ22δ12 的
1
−
α
1 - \alpha
1−α 的置信区间为
(
S
1
2
S
2
2
1
F
α
2
(
n
1
−
1
,
n
2
−
1
)
,
S
1
2
S
2
2
1
F
1
−
α
2
(
n
1
−
1
,
n
2
−
1
)
)
(\frac{S_1^2}{S_2^2}\frac{1}{F_{\frac{\alpha}{2}}(n_1 - 1, n_2 - 1)}, \frac{S_1^2}{S_2^2}\frac{1}{F_{1 - \frac{\alpha}{2}}(n_1 - 1, n_2 - 1)})
(S22S12F2α(n1−1,n2−1)1,S22S12F1−2α(n1−1,n2−1)1)
4. 假设检验
4.1 两个正态总体的均值和方差相等的检验
4.1.1 两个正态总体均值的检验, δ 1 2 = δ 2 2 \delta^2_1 = \delta^2_2 δ12=δ22 未知的情况 (t 分布)
H
0
H_0
H0 统计量为
T
=
X
ˉ
−
Y
ˉ
S
w
1
n
1
+
1
n
2
∼
t
(
n
1
+
n
2
−
2
)
T = \frac{\bar{X} - \bar{Y}}{S_w\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} \sim t(n_1 + n_2 - 2)
T=Swn11+n21Xˉ−Yˉ∼t(n1+n2−2)
其中
S
w
S_w
Sw 为
(
n
1
−
1
)
S
1
2
+
(
n
2
−
1
)
S
2
2
n
1
+
n
2
−
2
\sqrt{\frac{(n_1 - 1)S_1^2 + (n_2 - 1)S_2^2}{n_1 + n_2 - 2}}
n1+n2−2(n1−1)S12+(n2−1)S22
H
0
:
μ
1
=
μ
2
,
H
1
:
μ
1
≠
μ
2
H_0:\mu_1 = \mu_2, H_1:\mu_1 \ne \mu_2
H0:μ1=μ2,H1:μ1=μ2 称为双边检验,
H
0
H_0
H0 拒绝域为
∣
T
0
∣
≥
t
α
2
(
n
1
+
n
2
−
2
)
|T_0| \ge t_{\frac{\alpha}{2}}(n_1 + n_2 - 2)
∣T0∣≥t2α(n1+n2−2)
H
0
:
μ
1
=
μ
2
,
H
1
:
μ
1
>
μ
2
H_0:\mu_1 = \mu_2, H_1:\mu_1 \gt \mu_2
H0:μ1=μ2,H1:μ1>μ2 称为右边检验,
H
0
H_0
H0 拒绝域为
T
0
≥
t
α
(
n
1
+
n
2
−
2
)
T_0 \ge t_{\alpha}(n_1 + n_2 - 2)
T0≥tα(n1+n2−2)
H
0
:
μ
1
=
μ
2
,
H
1
:
μ
1
<
μ
2
H_0:\mu_1 = \mu_2, H_1:\mu_1 \lt \mu_2
H0:μ1=μ2,H1:μ1<μ2 称为左边检验,
H
0
H_0
H0 拒绝域为
T
0
≤
−
t
α
(
n
1
+
n
2
−
2
)
T_0 \le - t_{\alpha}(n_1 + n_2 - 2)
T0≤−tα(n1+n2−2)
4.1.2 两个正态总体方差相等的检验, δ 1 2 = δ 2 2 \delta^2_1 = \delta^2_2 δ12=δ22 (F 分布)
H
0
H_0
H0 统计量为
F
=
S
1
2
S
2
2
∼
F
(
n
1
−
1
,
n
2
−
1
)
F = \frac{S^2_1}{S^2_2} \sim F(n_1 - 1, n_2 - 1)
F=S22S12∼F(n1−1,n2−1)
H
0
:
δ
1
2
=
δ
2
2
,
H
1
:
δ
1
2
≠
δ
2
2
H_0:\delta_1^2 = \delta_2^2, H_1:\delta_1^2 \ne \delta_2^2
H0:δ12=δ22,H1:δ12=δ22 称为双边检验,
H
0
H_0
H0 拒绝域为
F
0
≥
F
α
2
(
n
1
−
1
,
n
2
−
1
)
F_0 \ge F_{\frac{\alpha}{2}}(n_1 - 1, n_2 - 1)
F0≥F2α(n1−1,n2−1) 或
F
0
≤
F
1
−
α
2
(
n
1
−
1
,
n
2
−
1
)
F_0 \le F_{1 - \frac{\alpha}{2}}(n_1 - 1, n_2 - 1)
F0≤F1−2α(n1−1,n2−1)
H
0
:
δ
1
2
=
δ
2
2
,
H
1
:
δ
1
2
>
δ
2
2
H_0:\delta_1^2 = \delta_2^2, H_1:\delta_1^2 \gt \delta_2^2
H0:δ12=δ22,H1:δ12>δ22 称为右边检验,
H
0
H_0
H0 拒绝域为
F
0
≥
F
α
(
n
1
−
1
,
n
2
−
1
)
F_0 \ge F_{\alpha}(n_1 - 1, n_2 - 1)
F0≥Fα(n1−1,n2−1)
H
0
:
δ
1
2
=
δ
2
2
,
H
1
:
δ
1
2
<
δ
2
2
H_0:\delta_1^2 = \delta_2^2, H_1:\delta_1^2 \lt \delta_2^2
H0:δ12=δ22,H1:δ12<δ22 称为左边检验,
H
0
H_0
H0 拒绝域为
F
0
≤
F
1
−
α
(
n
1
−
1
,
n
2
−
1
)
F_0 \le F_{1 - \alpha}(n_1 - 1, n_2 - 1)
F0≤F1−α(n1−1,n2−1)
4.2 列联表的独立检验
先求出
χ
0
2
\chi^2_0
χ02
χ
0
2
=
(
f
11
−
s
u
m
(
i
1
)
×
s
u
m
(
j
1
)
N
)
2
s
u
m
(
i
1
)
×
s
u
m
(
j
1
)
N
+
(
f
12
−
s
u
m
(
i
1
)
×
s
u
m
(
j
2
)
N
)
2
s
u
m
(
i
1
)
×
s
u
m
(
j
2
)
N
+
.
.
.
+
(
f
n
m
−
s
u
m
(
i
n
)
×
s
u
m
(
j
m
)
N
)
2
s
u
m
(
i
n
)
×
s
u
m
(
j
m
)
N
\chi^2_0 = \frac{(f_{11} - \frac{sum(i_1)\times sum(j_1)}{N})^2}{\frac{sum(i_1)\times sum(j_1)}{N}} + \frac{(f_{12} - \frac{sum(i_1)\times sum(j_2)}{N})^2}{\frac{sum(i_1)\times sum(j_2)}{N}} + ... + \frac{(f_{nm} - \frac{sum(i_n)\times sum(j_m)}{N})^2}{\frac{sum(i_n)\times sum(j_m)}{N}}
χ02=Nsum(i1)×sum(j1)(f11−Nsum(i1)×sum(j1))2+Nsum(i1)×sum(j2)(f12−Nsum(i1)×sum(j2))2+...+Nsum(in)×sum(jm)(fnm−Nsum(in)×sum(jm))2
其中,
f
i
j
f_{ij}
fij 为表格第
i
i
i 行第
j
j
j 列数据,
s
u
m
(
i
1
)
sum(i_1)
sum(i1) 表示第 1 行数据的和,
s
u
m
(
j
1
)
sum(j_1)
sum(j1) 表示第 1 列数据求和,
N
N
N 表示所有数据的和。
与 χ α 2 ( ( n − 1 ) ( m − 1 ) ) \chi^2_\alpha ((n - 1)(m - 1)) χα2((n−1)(m−1)) 相比较,
H 0 : 两 个 分 类 变 量 之 间 相 互 独 立 , H 1 : 两 个 分 类 变 量 之 间 不 独 立 H_0: 两个分类变量之间相互独立, H_1: 两个分类变量之间不独立 H0:两个分类变量之间相互独立,H1:两个分类变量之间不独立,若 χ 0 2 ≥ χ α 2 ( ( n − 1 ) ( m − 1 ) ) \chi^2_0 \ge \chi^2_\alpha ((n - 1)(m - 1)) χ02≥χα2((n−1)(m−1)),拒绝原假设 H 0 H_0 H0,即两个分类变量之间不相互独立(两个分类变量有联系)。
χ 0 2 \chi^2_0 χ02 越大,两个分类变量之间有联系的可能性就越大。
特殊情况

χ
2
=
n
(
a
d
−
b
c
)
2
(
a
+
c
)
(
b
+
d
)
(
a
+
b
)
(
c
+
d
)
\chi^2 = \frac{n(ad-bc)^2}{(a+c)(b+d)(a+b)(c+d)}
χ2=(a+c)(b+d)(a+b)(c+d)n(ad−bc)2
5. 方差分析
5.1 单因子方差分析的思想和单因子方差分析表
5.1.1 单因子方差分析的步骤
1)总偏差平方和的分解
试验考察的因素 A A A 有 s s s 个水平,在水平 A j ( j = 1 , 2 , . . . , s ) A_j(j = 1, 2, ..., s) Aj(j=1,2,...,s) 下,进行了 n j ( n j ≥ 2 ) n_j(n_j \ge 2) nj(nj≥2) 次实验。
设数据总平均为
X
ˉ
=
1
n
∑
j
=
1
s
∑
i
=
1
n
j
X
i
j
,
其
中
总
样
本
数
n
=
∑
j
=
1
s
n
j
\bar{X} = \frac{1}{n}\sum_{j=1}^{s}\sum_{i=1}^{n_j}X_{ij}, 其中总样本数 n=\sum_{j=1}^{s}n_j
Xˉ=n1j=1∑si=1∑njXij,其中总样本数n=j=1∑snj
引入
S
S
T
SST
SST 总偏差平方和(又称总变差)
S
S
T
=
∑
j
=
1
s
∑
i
=
1
n
j
(
X
i
j
−
X
ˉ
)
2
SST = \sum_{j=1}^{s}\sum_{i=1}^{n_j}(X_{ij} - \bar{X})^2
SST=j=1∑si=1∑nj(Xij−Xˉ)2
记水平
A
j
A_j
Aj 下的样本均值为
X
ˉ
∙
j
\bar{X}_{\bullet j}
Xˉ∙j,即
X
ˉ
∙
j
=
1
n
j
∑
i
=
1
n
j
X
i
j
\bar{X}_{\bullet j} = \frac{1}{n_j}\sum_{i=1}^{n_j}X_{ij}
Xˉ∙j=nj1i=1∑njXij
因为
S
S
T
=
∑
j
=
1
s
∑
i
=
1
n
j
(
X
i
j
−
X
ˉ
)
2
=
∑
j
=
1
s
∑
i
=
1
n
j
[
(
X
i
j
−
X
ˉ
∙
j
)
+
(
X
ˉ
∙
j
−
X
ˉ
)
]
2
SST = \sum_{j=1}^{s}\sum_{i=1}^{n_j}(X_{ij} - \bar{X})^2 = \sum_{j=1}^{s}\sum_{i=1}^{n_j}[(X_{ij} - \bar{X}_{\bullet j}) + (\bar{X}_{\bullet j} - \bar{X})]^2
SST=j=1∑si=1∑nj(Xij−Xˉ)2=j=1∑si=1∑nj[(Xij−Xˉ∙j)+(Xˉ∙j−Xˉ)]2
记
S
S
T
=
S
S
E
+
S
S
A
S
S
E
=
∑
j
=
1
s
∑
i
=
1
n
j
(
X
i
j
−
X
ˉ
∙
j
)
2
S
S
A
=
∑
j
=
1
s
∑
i
=
1
n
j
(
X
ˉ
∙
j
−
X
ˉ
)
2
SST = SSE + SSA \\ SSE = \sum_{j=1}^{s}\sum_{i=1}^{n_j}(X_{ij} - \bar{X}_{\bullet j})^2 \\ SSA = \sum_{j=1}^{s}\sum_{i=1}^{n_j}(\bar{X}_{\bullet j} - \bar{X})^2
SST=SSE+SSASSE=j=1∑si=1∑nj(Xij−Xˉ∙j)2SSA=j=1∑si=1∑nj(Xˉ∙j−Xˉ)2
称
S
S
E
SSE
SSE 为误差平方和,反应随机误差引起的波动,也称组内偏差平方和。
称
S
S
A
SSA
SSA 为效应平方和,反应因素
A
A
A 的水平变化引起的波动,也称组间偏差平方和或者因素平方和。
2)计算自由度和方差(平均偏差平方和)
S
S
T
SST
SST 的自由度为
f
T
=
n
−
1
f_T = n - 1
fT=n−1
S
S
A
SSA
SSA 的自由度为
f
A
=
s
−
1
f_A = s - 1
fA=s−1
S
S
E
SSE
SSE 的自由度为
f
e
=
n
−
s
f_e = n - s
fe=n−s
f e 可 以 通 过 f e = f T − f A 求 出 f_e 可以通过 f_e = f_T - f_A 求出 fe可以通过fe=fT−fA求出
求出
S
S
A
SSA
SSA 和
S
S
E
SSE
SSE 的平均值:
M
S
A
=
S
S
A
/
f
A
M
S
E
=
S
S
E
/
f
e
MSA = SSA/f_A \\ MSE = SSE/f_e
MSA=SSA/fAMSE=SSE/fe
M
S
A
MSA
MSA 称为组间方差,
M
S
E
MSE
MSE 称为组内方差。
3)显著性检验
H 0 : μ 1 = μ 2 = . . . = μ s , H 1 : μ 1 , μ 2 , . . . , μ s H_0: \mu_1 = \mu_2 = ... = \mu_s, H_1: \mu_1, \mu_2, ..., \mu_s H0:μ1=μ2=...=μs,H1:μ1,μ2,...,μs 不全相等
统计量
F
0
F_0
F0
F
0
=
S
S
A
/
(
s
−
1
)
S
S
E
/
(
n
−
s
)
=
M
S
A
M
S
E
∼
F
(
s
−
1
,
n
−
s
)
F_0 = \frac{SSA/(s-1)}{SSE/(n-s)} = \frac{MSA}{MSE} \sim F(s-1, n-s)
F0=SSE/(n−s)SSA/(s−1)=MSEMSA∼F(s−1,n−s)
若
F
0
≥
F
α
F_0 \ge F_\alpha
F0≥Fα,则拒绝原假设,即认为因素
A
A
A 对试验结果有显著影响;
若
F
0
<
F
α
F_0 \lt F_\alpha
F0<Fα,则接受原假设,即认为因素
A
A
A 对试验结果无显著影响。
检验水平
α
\alpha
α 的选取视具体情况而定,通常取
α
=
0.01
,
α
=
0.05
\alpha = 0.01,\alpha = 0.05
α=0.01,α=0.05,
若
F
0
≥
F
0.01
F_0 \ge F_{0.01}
F0≥F0.01 ,判定因素
A
A
A 为高度显著,
若
F
0.01
>
F
0
≥
F
0.05
F_{0.01} \gt F_0 \ge F_{0.05}
F0.01>F0≥F0.05 ,判定因素
A
A
A 为显著,
若
F
0
<
F
0.05
F_0 \lt F_{0.05}
F0<F0.05 ,判定因素
A
A
A 为不显著,
4)列出方差分析表
| 方差来源 | 偏差平方和 | 自由度 | 方差 | F值 | F α F_\alpha Fα | 显著性 |
|---|---|---|---|---|---|---|
| 因素A(组间) | SSA | s - 1 | M S A = S S A s − 1 MSA = \frac{SSA}{s - 1} MSA=s−1SSA | F = M S A M S E F = \frac{MSA}{MSE} F=MSEMSA | 查表 | |
| 误差e(组内) | SSE | n - s | M S E = S S E n − s MSE = \frac{SSE}{n - s} MSE=n−sSSE | |||
| 总和 | SST | n - 1 |
MatLab 中的例子:
[p, anovatab, stats] = anova1(X, group, 'displayopt')

方差分析表例子:
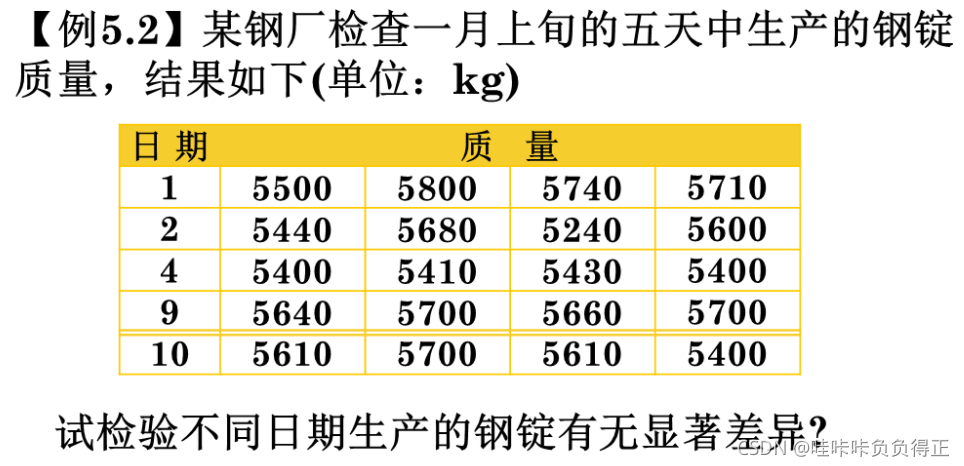
X = [
5500 5800 5740 5710;
5440 5680 5240 5600;
5400 5410 5430 5400;
5640 5700 5660 5700;
5610 5700 5610 5400
];
% 因为参数要求每列为一组,故需要将 X 进行转置
[p, table, stats] = anova1(X', [], 'on');
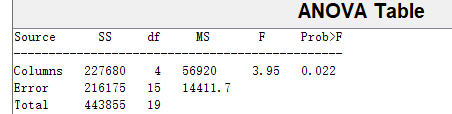
图中 p = 0.022 < α = 0.05 p = 0.022 \lt \alpha = 0.05 p=0.022<α=0.05,故判定日期因素对生产质量有显著影响。
5.2 写出有交互作用的双因子方差分析 Matlab 命令并分析结果含义
[p, Table] = anova2(X, reps, 'off')

有交互作用的双因子方差分析表,其中
n
n
n 为
r
e
p
s
reps
reps 单元观测点数目,也就是每种条件下重复试验的次数。

下面这个网站有例子:
https://www.cnblogs.com/begtostudy/archive/2012/06/22/2558974.html
这个网站里面有 anova2 函数的详细介绍
https://ww2.mathworks.cn/help/stats/anova2.html
输入格式
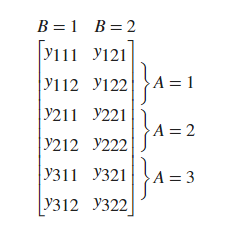
方差分析表例子:
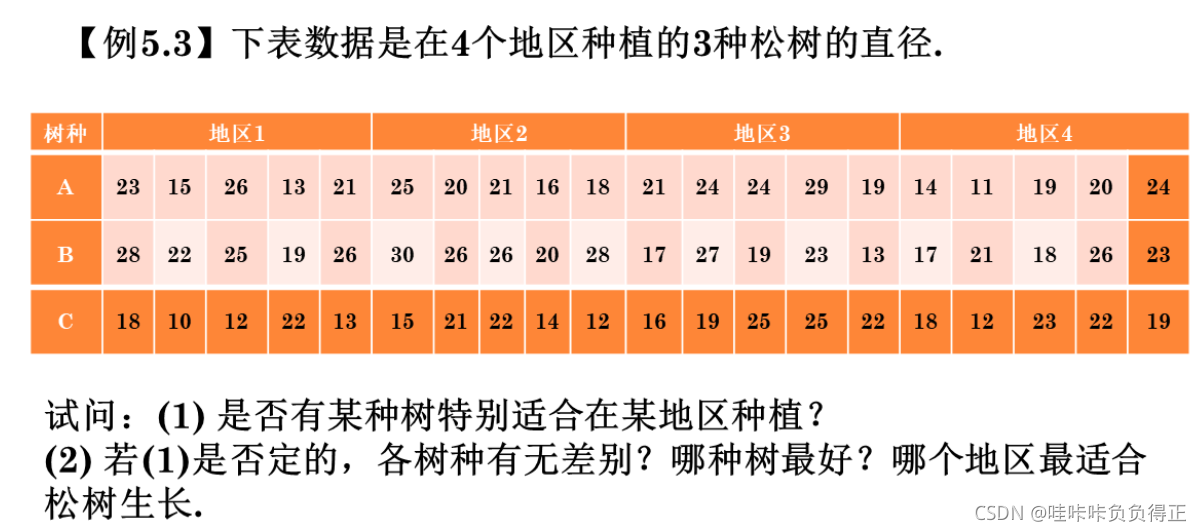
X = [
23 15 26 13 21 25 20 21 16 18 21 24 24 29 19 14 11 19 20 24
28 22 25 19 26 30 26 26 20 28 17 27 19 23 13 17 21 18 26 23
18 10 12 22 13 15 21 22 14 12 16 19 25 25 22 18 12 23 22 19
];
% 根据参数要求,对 X 进行转置, 第二个参数是每次测量数据数
[p, table, stats] = anova2(X', 5, 'on');

p
A
=
0.0055
<
0.05
p_A = 0.0055 < 0.05
pA=0.0055<0.05,树种因素对结果有显著影响;
p
B
=
0.3944
>
0.05
p_B = 0.3944 > 0.05
pB=0.3944>0.05,地区因素对结果无显著影响;
p
A
B
=
0.0508
>
0.05
p_{AB} = 0.0508 > 0.05
pAB=0.0508>0.05,树种和地区因素交互作用无显著影响,所以没有某种树种特别适合在某地区种植。
6. 回归分析
6.1 写出回归分析的 Matlab 命令并分析结果含义
[b, bint, r, rint, stats] = regress(y, X, 0.05)
b 为回归系数
bint 为回归系数的置信区间
r 为残差,代表实际值与估计值的差
rint 为残差置信区间
stats 用于检验回归模型的统计量,四个数值分别为 决定系数
R
2
=
S
S
R
S
S
T
R^2=\frac{SSR}{SST}
R2=SSTSSR(越接近 1 越好),F 值(越大越好),p值(越小越拒绝,越好),误差无偏估计

X 必须包含一列 1,以便模型包含常数项。
这个网站有解释
https://ww2.mathworks.cn/help/stats/regress.html
例子
https://blog.csdn.net/guzhenping/article/details/43314333


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










