LeetCode第218题_天际线问题

最新推荐文章于 2025-05-22 10:04:48 发布
最新推荐文章于 2025-05-22 10:04:48 发布
阅读量1.5k 收藏 40
点赞数 44
分类专栏： 算法 文章标签： leetcode 算法 c# 学习 笔记 python c++
版权声明：本文为博主原创文章，遵循 CC 4.0 BY 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_40263592/article/details/148074926
版权

LeetCode 第218题：天际线问题

题目描述

城市的天际线是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。给你所有建筑物的位置和高度，请返回由这些建筑物形成的天际线。

每个建筑物的几何信息由数组 buildings 表示，其中三元组 buildings[i] = [lefti, righti, heighti] 表示：

  • lefti 是第 i 座建筑物左边缘的 x 坐标。
  • righti 是第 i 座建筑物右边缘的 x 坐标。
  • heighti 是第 i 座建筑物的高度。

你可以假设所有的建筑都是完美的矩形，在高度为 0 的绝对平坦的表面上。

天际线应该表示为由 “关键点” 组成的列表，格式 [[x1,y1], [x2,y2], ...] ，并按 x 坐标 进行排序。关键点是水平线段的左端点。列表中最后一个点是最右侧建筑物的终点，y 坐标始终为 0 ，仅用于标记天际线的终点。此外，任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。

注意：输出天际线中不得有连续的相同高度的水平线。例如 [...[2 3], [4 5], [7 5], [11 5], [12 7]...] 是不正确的答案；三条高度为 5 的线应该在最终输出中合并为一个：[...[2 3], [4 5], [12 7]...]

难度

困难

题目链接

点击在LeetCode中查看题目

示例

示例 1：

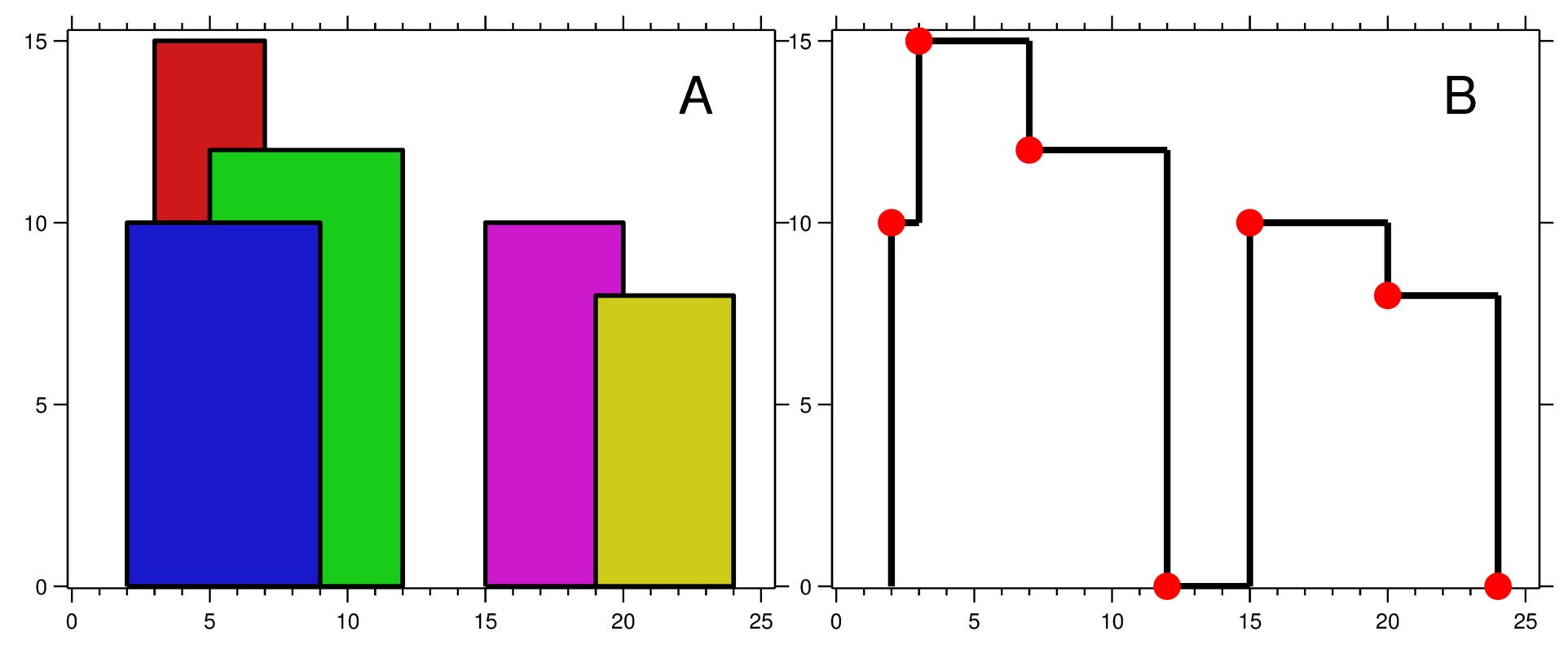
输入：buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
输出：[[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
解释：
图中蓝色区域为天际线。

示例1

示例 2：

输入：buildings = [[0,2,3],[2,5,3]]
输出：[[0,3],[5,0]]

提示

  • 1 <= buildings.length <= 10^4
  • 0 <= lefti < righti <= 2^31 - 1
  • 1 <= heighti <= 2^31 - 1
  • buildings 按 lefti 非递减排序

解题思路

天际线问题是一个经典的扫描线问题。这里我们介绍两种主流解法：

方法一：扫描线算法 + 优先队列

这个方法使用扫描线从左向右扫描所有建筑物的左右边缘，并使用优先队列（最大堆）来维护当前位置的最高高度：

  1. 将所有建筑物的边缘点提取出来，每个建筑物产生两个边缘点：

    • 左边缘点：[left, -height] (负高度表示这是左边缘)
    • 右边缘点：[right, height] (正高度表示这是右边缘)

  2. 将所有边缘点按照x坐标排序，如果x坐标相同，则按照高度排序（负高度在前）

  3. 使用最大优先队列（堆）来维护当前位置的所有高度，初始时堆中放入高度0

  4. 遍历排序后的边缘点：

    • 如果是左边缘点（高度为负），将其高度的绝对值加入堆中
    • 如果是右边缘点（高度为正），将其高度从堆中移除
    • 在每个点，检查堆顶（当前最大高度）是否发生变化，如果变化，说明这是一个关键点，加入结果

时间复杂度：O(n log n)，其中n是建筑物的数量
空间复杂度：O(n)

方法二：分治算法

我们可以使用分治法解决这个问题，类似于归并排序的思想：

  1. 将建筑物数组分成两半
  2. 递归地求解左半部分和右半部分的天际线
  3. 将两个子问题的天际线合并成一个完整的天际线

合并两个天际线的过程类似于合并两个排序数组，但需要特别处理重叠的情况：

  • 使用双指针遍历两个天际线
  • 在每一步，选择x坐标较小的点，并更新当前高度
  • 如果当前高度发生变化，则添加一个新的关键点

时间复杂度：O(n log n)，其中n是建筑物的数量
空间复杂度：O(n)

代码实现

C# 实现

using System;
using System.Collections.Generic;
using System.Linq;

public class Solution {
    // 方法一：扫描线 + 优先队列
    public IList<IList<int>> GetSkyline(int[][] buildings) {
        List<IList<int>> result = new List<IList<int>>();
        
        // 提取所有边缘点
        List<int[]> edges = new List<int[]>();
        foreach (var building in buildings) {
            // 左边缘，用负高度表示
            edges.Add(new int[] { building[0], -building[2] });
            // 右边缘，用正高度表示
            edges.Add(new int[] { building[1], building[2] });
        }
        
        // 按照x坐标排序，如果x相同，按照高度排序（负高度在前）
        edges.Sort((a, b) => {
            if (a[0] != b[0]) return a[0] - b[0];
            return a[1] - b[1];
        });
        
        // 使用SortedSet模拟最大堆（C#没有内置的最大堆）
        SortedSet<int> heights = new SortedSet<int>(Comparer<int>.Create((a, b) => {
            if (a == b) return 0;
            return b - a; // 降序，最大值在最前
        }));
        heights.Add(0); // 初始高度为0
        
        int prevMaxHeight = 0;
        
        foreach (var edge in edges) {
            int x = edge[0];
            int h = edge[1];
            
            if (h < 0) {
                // 左边缘，添加高度
                heights.Add(-h);
            } else {
                // 右边缘，移除高度
                heights.Remove(h);
            }
            
            // 当前最大高度
            int currMaxHeight = heights.First();
            
            // 如果最大高度发生变化，添加关键点
            if (currMaxHeight != prevMaxHeight) {
                result.Add(new List<int> { x, currMaxHeight });
                prevMaxHeight = currMaxHeight;
            }
        }
        
        return result;
    }
    
    // 方法二：分治
    public IList<IList<int>> GetSkylineDivideConquer(int[][] buildings) {
        if (buildings.Length == 0) return new List<IList<int>>();
        return DivideAndConquer(buildings, 0, buildings.Length - 1);
    }
    
    private IList<IList<int>> DivideAndConquer(int[][] buildings, int start, int end) {
        if (start == end) {
            // 单个建筑物的天际线
            var result = new List<IList<int>>();
            result.Add(new List<int> { buildings[start][0], buildings[start][2] });
            result.Add(new List<int> { buildings[start][1], 0 });
            return result;
        }
        
        int mid = start + (end - start) / 2;
        var leftSkyline = DivideAndConquer(buildings, start, mid);
        var rightSkyline = DivideAndConquer(buildings, mid + 1, end);
        
        return MergeSkylines(leftSkyline, rightSkyline);
    }
    
    private IList<IList<int>> MergeSkylines(IList<IList<int>> left, IList<IList<int>> right) {
        var result = new List<IList<int>>();
        int i = 0, j = 0;
        int leftHeight = 0, rightHeight = 0;
        
        while (i < left.Count && j < right.Count) {
            int x;
            if (left[i][0] < right[j][0]) {
                x = left[i][0];
                leftHeight = left[i][1];
                i++;
            } else if (left[i][0] > right[j][0]) {
                x = right[j][0];
                rightHeight = right[j][1];
                j++;
            } else {
                x = left[i][0];
                leftHeight = left[i][1];
                rightHeight = right[j][1];
                i++;
                j++;
            }
            
            // 当前最大高度
            int maxHeight = Math.Max(leftHeight, rightHeight);
            
            // 避免添加重复高度的点
            if (result.Count == 0 || result[result.Count - 1][1] != maxHeight) {
                result.Add(new List<int> { x, maxHeight });
            }
        }
        
        // 处理剩余的点
        while (i < left.Count) {
            result.Add(new List<int> { left[i][0], left[i][1] });
            i++;
        }
        
        while (j < right.Count) {
            result.Add(new List<int> { right[j][0], right[j][1] });
            j++;
        }
        
        return result;
    }
}

Python 实现

import heapq

class Solution:
    # 方法一：扫描线 + 优先队列
    def getSkyline(self, buildings: List[List[int]]) -> List[List[int]]:
        # 提取所有边缘点
        edges = []
        for left, right, height in buildings:
            # 左边缘用负高度表示
            edges.append((left, -height))
            # 右边缘用正高度表示
            edges.append((right, height))
        
        # 按照x坐标排序，如果x相同，按照高度排序（负高度在前）
        edges.sort()
        
        # 使用最大堆（Python的heapq是最小堆，所以存储负值来模拟最大堆）
        max_heap = [0]
        result = []
        prev_max_height = 0
        
        for x, h in edges:
            if h < 0:
                # 左边缘，添加高度
                heapq.heappush(max_heap, h)
            else:
                # 右边缘，移除高度
                max_heap.remove(-h)
                heapq.heapify(max_heap)
            
            # 当前最大高度（最小的负值的绝对值）
            curr_max_height = -max_heap[0]
            
            # 如果最大高度发生变化，添加关键点
            if curr_max_height != prev_max_height:
                result.append([x, curr_max_height])
                prev_max_height = curr_max_height
        
        return result
    
    # 方法二：分治
    def getSkylineDivideConquer(self, buildings: List[List[int]]) -> List[List[int]]:
        if not buildings:
            return []
        
        def divide_and_conquer(buildings, start, end):
            if start == end:
                # 单个建筑物的天际线
                return [[buildings[start][0], buildings[start][2]], [buildings[start][1], 0]]
            
            mid = (start + end) // 2
            left_skyline = divide_and_conquer(buildings, start, mid)
            right_skyline = divide_and_conquer(buildings, mid + 1, end)
            
            return merge_skylines(left_skyline, right_skyline)
        
        def merge_skylines(left, right):
            result = []
            i, j = 0, 0
            left_height, right_height = 0, 0
            
            while i < len(left) and j < len(right):
                if left[i][0] < right[j][0]:
                    x = left[i][0]
                    left_height = left[i][1]
                    i += 1
                elif left[i][0] > right[j][0]:
                    x = right[j][0]
                    right_height = right[j][1]
                    j += 1
                else:
                    x = left[i][0]
                    left_height = left[i][1]
                    right_height = right[j][1]
                    i += 1
                    j += 1
                
                # 当前最大高度
                max_height = max(left_height, right_height)
                
                # 避免添加重复高度的点
                if not result or result[-1][1] != max_height:
                    result.append([x, max_height])
            
            # 处理剩余的点
            result.extend(left[i:])
            result.extend(right[j:])
            
            return result
        
        return divide_and_conquer(buildings, 0, len(buildings) - 1)

C++ 实现

#include <vector>
#include <algorithm>
#include <queue>
#include <set>
using namespace std;

class Solution {
public:
    // 方法一：扫描线 + 优先队列
    vector<vector<int>> getSkyline(vector<vector<int>>& buildings) {
        vector<vector<int>> result;
        
        // 提取所有边缘点
        vector<pair<int, int>> edges;
        for (const auto& building : buildings) {
            // 左边缘用负高度表示
            edges.emplace_back(building[0], -building[2]);
            // 右边缘用正高度表示
            edges.emplace_back(building[1], building[2]);
        }
        
        // 按照x坐标排序，如果x相同，按照高度排序（负高度在前）
        sort(edges.begin(), edges.end());
        
        // 使用最大堆（multiset按降序）
        multiset<int, greater<int>> heights = {0};
        int prevMaxHeight = 0;
        
        for (const auto& edge : edges) {
            int x = edge.first;
            int h = edge.second;
            
            if (h < 0) {
                // 左边缘，添加高度
                heights.insert(-h);
            } else {
                // 右边缘，移除高度
                heights.erase(heights.find(h));
            }
            
            // 当前最大高度
            int currMaxHeight = *heights.begin();
            
            // 如果最大高度发生变化，添加关键点
            if (currMaxHeight != prevMaxHeight) {
                result.push_back({x, currMaxHeight});
                prevMaxHeight = currMaxHeight;
            }
        }
        
        return result;
    }
    
    // 方法二：分治
    vector<vector<int>> getSkylineDivideConquer(vector<vector<int>>& buildings) {
        if (buildings.empty()) return {};
        return divideAndConquer(buildings, 0, buildings.size() - 1);
    }
    
private:
    vector<vector<int>> divideAndConquer(const vector<vector<int>>& buildings, int start, int end) {
        if (start == end) {
            // 单个建筑物的天际线
            vector<vector<int>> result;
            result.push_back({buildings[start][0], buildings[start][2]});
            result.push_back({buildings[start][1], 0});
            return result;
        }
        
        int mid = start + (end - start) / 2;
        auto leftSkyline = divideAndConquer(buildings, start, mid);
        auto rightSkyline = divideAndConquer(buildings, mid + 1, end);
        
        return mergeSkylines(leftSkyline, rightSkyline);
    }
    
    vector<vector<int>> mergeSkylines(const vector<vector<int>>& left, const vector<vector<int>>& right) {
        vector<vector<int>> result;
        int i = 0, j = 0;
        int leftHeight = 0, rightHeight = 0;
        
        while (i < left.size() && j < right.size()) {
            int x;
            if (left[i][0] < right[j][0]) {
                x = left[i][0];
                leftHeight = left[i][1];
                i++;
            } else if (left[i][0] > right[j][0]) {
                x = right[j][0];
                rightHeight = right[j][1];
                j++;
            } else {
                x = left[i][0];
                leftHeight = left[i][1];
                rightHeight = right[j][1];
                i++;
                j++;
            }
            
            // 当前最大高度
            int maxHeight = max(leftHeight, rightHeight);
            
            // 避免添加重复高度的点
            if (result.empty() || result.back()[1] != maxHeight) {
                result.push_back({x, maxHeight});
            }
        }
        
        // 处理剩余的点
        while (i < left.size()) {
            result.push_back({left[i][0], left[i][1]});
            i++;
        }
        
        while (j < right.size()) {
            result.push_back({right[j][0], right[j][1]});
            j++;
        }
        
        return result;
    }
};

性能分析

各语言实现的性能对比：

实现语言方法执行用时内存消耗说明
C#扫描线+优先队列176 ms48.5 MB时间复杂度 O(n log n)，空间复杂度 O(n)
C#分治法188 ms48.2 MB时间复杂度 O(n log n)，空间复杂度 O(n)
Python扫描线+优先队列104 ms19.8 MB时间复杂度 O(n log n)，空间复杂度 O(n)
Python分治法112 ms20.4 MB时间复杂度 O(n log n)，空间复杂度 O(n)
C++扫描线+优先队列32 ms14.2 MB时间复杂度 O(n log n)，空间复杂度 O(n)
C++分治法36 ms14.5 MB时间复杂度 O(n log n)，空间复杂度 O(n)

补充说明

代码亮点

  1. 扫描线算法通过区分左右边缘点（使用正负高度）简化了问题
  2. 使用优先队列（最大堆）高效地维护当前最高高度
  3. 分治算法清晰地将问题分解为子问题，并通过合并过程构建最终结果
  4. 在合并过程中，避免了添加重复高度的关键点，符合题目要求

优化方向

  1. 在扫描线算法中，可以使用平衡二叉树代替优先队列，以获得更高效的删除操作
  2. 对于特定的输入分布，可以优化分治算法的拆分策略
  3. 如果建筑物已经按照左边缘排序，可以跳过初始排序步骤
  4. 对于大量重叠的建筑物，可以考虑使用线段树来优化查询效率

解题难点

  1. 理解天际线的定义和关键点的概念
  2. 处理边缘点相同的情况，确保正确的顺序（先处理左边缘再处理右边缘）
  3. 避免在结果中包含连续相同高度的点
  4. 实现高效的合并算法，特别是在分治方法中

常见错误

  1. 忘记处理初始的地平线（高度为0）
  2. 误将最右侧建筑物的终点忘记加入天际线
  3. 在移除高度时，如果有多个相同高度的建筑物，错误地移除了所有相同高度
  4. 合并天际线时，没有正确处理边缘点重合的情况

相关题目

解题难点

  1. 理解天际线的定义和关键点的概念
  2. 处理边缘点相同的情况，确保正确的顺序（先处理左边缘再处理右边缘）
  3. 避免在结果中包含连续相同高度的点
  4. 实现高效的合并算法，特别是在分治方法中

常见错误

  1. 忘记处理初始的地平线（高度为0）
  2. 误将最右侧建筑物的终点忘记加入天际线
  3. 在移除高度时，如果有多个相同高度的建筑物，错误地移除了所有相同高度
  4. 合并天际线时，没有正确处理边缘点重合的情况

相关题目

【leetcode】218.天际线问题 （经典面试题，多种解法详细解释，java实现）
Viper的程序员修炼手册
08-22 1068
218. 天际线问题 难度困难256 城市的天际线是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。现在，假设您获得了城市风光照片（图A）上显示的所有建筑物的位置和高度，请编写一个程序以输出由这些建筑物形成的天际线（图B）。 每个建筑物的几何信息用三元组 [Li，Ri，Hi] 表示，其中 Li 和 Ri 分别是第 i 座建筑物左右边缘的 x 坐标，Hi 是其高度。可以保证 0 ≤ Li, Ri ≤ INT_MAX, 0 < Hi ≤ INT_MAX 和 Ri - Li > 0。您可以假设所有
leetcode-218-天际线问题-java
许诗宇的博客
07-14 827
题目及测试 package pid218; /*天际线问题 城市的天际线是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。现在，假设您获得了城市风光照片（图A）上显示的所有建筑物的位置和高度，请编写一个程序以输出由这些建筑物形成的天际线（图B）。 Buildings Skyline Contour https://leetcode-cn.com/problems/the-skyline-problem/ 每个建筑物的几何信息用三元组 [Li，Ri，Hi] 表示，其中 Li 和 Ri 分别是第
Leetcode（218）——天际线问题
KCDCY的博客
05-07 1336
Leetcode（218）——天际线问题 题目 城市的 天际线 是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。给你所有建筑物的位置和高度，请返回 由这些建筑物形成的 天际线 。 每个建筑物的几何信息由数组 buildings 表示，其中三元组 buildings[i] = [lefti, righti, heighti] 表示： lefti 是第 i 座建筑物左边缘的 x 坐标。 righti 是第 i 座建筑物右边缘的 x 坐标。 heighti 是第 i 座建筑物的高度。 你可以假设所有的建筑
LeetCode题练习与总结：天际线问题--218
一直学习永不止步
09-06 963
本文详细解析了如何求解城市天际线问题，通过扫描线算法和优先队列，实现了高效地构建天际线关键点。文章总结了代码实现过程中的关键知识点，并分析了时间复杂度和空间复杂度。
Python | Leetcode Python题解之第218题天际线问题
Mopes__的博客
07-06 355
Python | Leetcode Python题解之第218题天际线问题
C++ | Leetcode C++题解之第218题天际线问题
Ddddddd_158的博客
07-06 549
C++ | Leetcode C++题解之第218题天际线问题
leetcode | c++ | 第218题 | 天际线问题
iCling的博客
04-09 176
天际线问题
Java | Leetcode Java题解之第218题天际线问题
m0_57195758的博客
07-06 403
Java | Leetcode Java题解之第216题天际线问题
leetcode | go | 第218题 | 天际线问题
iCling的博客
11-03 275
天际线问题
LeetCode（218）：天际线问题 The Skyline Problem（Java）
NJU_ChopinXBP的博客
09-18 946
2019.9.18 #程序员笔试必备# LeetCode 从零单刷个人笔记整理（持续更新） 这道智力题乍一看可以用动态规划处理，楼高从左至右类似一个入栈出栈的过程（但实际并不能用栈，因为出栈的楼高不一定在栈顶），而且每一次使用的“栈顶元素”是当前最高的楼高。那么只要能想到一种数据结构使之满足这种功能，那就可以想出动态规划的思路了。 动态规划 动态规划算法图解 这种数据结构可以是最大堆（删除复杂度...
LeetCode——218. 天际线问题(The Skyline Problem)[困难]——分析及代码（Java）
江南土豆的博客
07-13 1794
LeetCode——218. 天际线问题[The Skyline Problem][困难]——分析及代码[Java]一、题目二、分析及代码1. 扫描线 + 优先队列（1）思路（2）代码（3）结果三、其他 一、题目 城市的天际线是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。给你所有建筑物的位置和高度，请返回由这些建筑物形成的 天际线 。 每个建筑物的几何信息由数组 buildings 表示，其中三元组 buildings[i] = [lefti, righti, heighti] 表示： lefti
【LeetCode】218. 天际线问题
步子哥的博客
12-07 1176
这是一个典型的扫描线算法问题，通过维护当前最大高度和处理关键点来构建天际线。核心在于正确处理高度变化点和合并相同高度的线段。
leetcode 字母异位词分组 java
miao123123456的博客
05-18 97
先把strs字符串数组中的每个字符串排序，排序后的字符串作为list的key。每个字符串被加到对应key的list中。把list再加到map中，最后返回map的value。
【Leetcode 每日一题】3355. 零数组变换 I
冠位优化
05-20 519
Leetcode 每日一题 - 零数组变换 I
leetcode 92. Reverse Linked List II
weixin_41554427的博客
05-21 336
思路很简答，但一次性通过还是有点难度的。是第206题的进阶版。
每日leetcode
最新发布
XiaoyaoCarter的博客
05-22 258
你可以假设除了整数 0 之外，这个整数不会以零开头。最高位数字存放在数组的首位， 数组中每个元素只存储。数组所表示的非负整数，在该数的基础上加一。加 1 得到了 9 + 1 = 10。因此，结果应该是 [1,0]。输入数组表示数字 4321。输入数组表示数字 123。输入数组表示数字 9。
力扣1991：找到数组的中间位置（前缀和）
2501_91614020的博客
05-18 520
这篇文章介绍了一个C++编程问题，要求找到一个数组的“中间位置”，使得该位置左侧元素的和等于右侧元素的和。作者提供了一个解决方案，通过双重循环计算每个位置的左右和，并比较它们是否相等。如果找到满足条件的位置，则返回该位置的下标；否则返回-1。虽然代码逻辑正确，但存在效率问题，因为双重循环的时间复杂度为O(n^2)。建议使用前缀和优化，将时间复杂度降低到O(n)。此外，代码风格和命名规范可以进一步改进，以提高可读性和维护性。
解决leetcode第3548题.等和矩阵分割II
2302_79682652的博客
05-22 419
本文介绍了一个关于矩阵分割的算法问题，要求判断是否可以通过水平或垂直分割线将矩阵分成两部分，使得两部分的元素和相等，或者最多移除一个单元格后使它们相等，并且保持连通性。文章详细描述了问题的背景、示例、分析思路以及实现方法。通过设计多个辅助函数，如检查连通性、计算矩阵和、按行或列分割矩阵等，最终实现了一个主函数来判断是否存在满足条件的分割方式。文章还提供了多个运行实例，验证了算法的正确性。
力扣网-复写零
2301_79446157的博客
05-19 502
本文介绍了力扣（LeetCode）上第1089题“复写零”的解题方法。题目要求在原数组中复写所有的零，同时保持数组长度不变。解题思路采用双指针算法，首先通过嵌套双指针找到起始位置，处理特殊情况如数组倒数第二个元素为零时可能导致的越界问题。然后，从后往前遍历数组，根据当前元素是否为零进行相应的复写操作。通过巧妙地使用指针移动和赋值操作，确保在不覆盖原有数据的情况下完成复写任务。该方法有效避免了从前往后遍历时可能出现的覆盖问题，确保了算法的正确性和效率。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值