目标检测算法实现（八）——YOLOV5学习笔记

是刺猬吖

已于 2022-04-21 15:18:46 修改

阅读量8.4k

点赞数 17

分类专栏： YOLO算法文章标签： python

于 2021-11-11 21:58:56 首次发布

本文链接：https://blog.csdn.net/qq_40305597/article/details/121268363

版权

YOLO算法专栏收录该内容

9 篇文章

订阅专栏

本文深入剖析YOLOv5的网络结构与优化策略，包括Mosaic数据增强、自适应锚框计算和自适应图片缩放等改进。详细介绍了YOLOv5s、m、l、x四种模型的差异，探讨了Focus结构、CSP结构、FPN+PAN结构以及各种损失函数的作用。此外，还解析了网络的宽度和深度控制，并解释了IoU、Precision、Recall等相关基础概念。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

非常感谢江大白大佬的研究与分享附链接
深入浅出Yolo系列之Yolov5核心基础知识完整讲解

2.4.1 Bounding box损失函数

1.网络结构图+v5性能对比

Yolov3的网络结构

Yolov4的网络结构

Yolov5s的网络结构

Yolov5官方代码中，给出的目标检测网络中一共有4个版本，分别是Yolov5s、Yolov5m、Yolov5l、Yolov5x四个模型。将yolov5s四种模型的pt文件转换成对应的onnx文件后，即可使用netron工具查看。Yolov5也是在COCO数据集上进行的测试。Yolov5s网络最小，速度最少，AP精度也最低。但如果检测的以大目标为主，追求速度，倒也是个不错的选择。（我这里使用的是yolov5s）其他的三种网络，在此基础上，不断加深加宽网络，AP精度也不断提升，但速度的消耗也在不断增加。效果对比如下图。

Yolov5的算法性能测试图

在这里插入图片描述

YOLOv5三种模型比较

2.v5的改进和优势

根据Yolov5的网络结构图，可以看出，还是分为输入端、Backbone、Neck、Prediction四个部分：
（1）输入端：Mosaic数据增强、自适应锚框计算
（2）Backbone：Focus结构，CSP结构
（3）Neck：FPN+PAN结构
（4）Prediction：GIOU_Loss

2.1 输入端

2.1.1 Mosaic数据增强

Yolov5的输入端采用了和Yolov4一样的Mosaic数据增强的方式。Mosaic数据增强随机选取4张图片进行随机缩放、随机裁剪、随机排布的方式进行拼接，对于小目标的检测效果还是很不错的。

2.1.2 自适应锚框计算

在Yolo算法中，针对不同的数据集，都会有初始设定长宽的锚框。在网络训练中，网络在初始锚框的基础上输出预测框，进而和真实框groundtruth进行比对，计算两者差距，再反向更新，迭代网络参数。Yolov5在Coco数据集上初始设定的锚框：

在这里插入图片描述

在Yolov3、Yolov4中，训练不同的数据集时，计算初始锚框的值是通过单独的程序运行的，Yolov5中将此功能嵌入到代码中，每次训练时，自适应的计算不同训练集中的最佳锚框值。如果计算的锚框效果不好，也可以在train.py中将该行设置成False，将自动计算锚框功能关闭。

在这里插入图片描述

2.1.3 自适应图片缩放

在常见的目标检测算法中，不同的图片长宽都不相同，常用方式是将原始图片统一缩放到一个标准尺寸（Yolo中常用416×416，608×608等尺寸），再送入检测网络中。eg. 在这里插入图片描述
很多图片的长宽比不同，缩放填充后两端的黑边大小都不同，而如果填充较多，则存在信息冗余影响推理速度，Yolov5代码中datasets.py的letterbox函数中进行了修改，对原始图像自适应的添加最少的黑边，推理时计算量会减少，目标检测速度会得到提升。

在这里插入图片描述

另：letterbox函数讲解：

第一步：计算缩放比例

原始缩放尺寸416×416除以原始图像的尺寸后得到0.52和0.69两个缩放系数，选择小的缩放系数。

第二步：计算缩放后的尺寸

在这里插入图片描述

原始图片的长宽都乘以最小的缩放系数0.52，宽变成了416，而高变成了312。

第三步：计算黑边填充数值

在这里插入图片描述

416-312=104得到原本需要填充的高度，采用numpy中np.mod取余数的方式，得到8个像素再除以2，得到图片高度两端需要填充的数值。

Attention：
a.这里填充的是黑色（0，0，0），而Yolov5中填充的是灰色（114,114,114），都是一样的效果。
b.训练时采用传统填充（416×416）的方式，检测使用模型推理时采用缩减黑边的方式，提高目标检测推理的速度。
c.np.mod函数的后面用32是因为Yolov5的网络经过5次下采样（2的5次方=32），所以至少要去掉32的倍数再进行取余。

2.2 Backbone

2.2.1 Focus结构

在这里插入图片描述

在Yolov3&Yolov4中并没有Focus结构，结构中比较关键是切片操作，4×4×3的图像切片后变成2×2×12的特征图。上图以Yolov5s的结构为例，原始608×608×3的图像输入Focus结构，采用切片操作变成304×304×12的特征图，再经过一次32个卷积核的卷积操作（其他三种结构使用的卷积核数量有所增加），最终变304×304×32的特征图。

2.2.2 CSP结构

Yolov4网络结构中借鉴了CSPNet的设计思路，在主干网络中设计了CSP结构。如下图：

在这里插入图片描述

Yolov5与Yolov4不同点在于，Yolov4中只有主干网络使用了CSP结构，Yolov5中设计了两种CSP结构，eg.Yolov5s.CSP1_X结构应用于Backbone主干网络，另一种CSP2_X结构则应用于Neck中。

在这里插入图片描述

补充学习：CSPNet（未学习）

CSPDarknet53是在Yolov3主干网络Darknet53的基础上借鉴2019年CSPNet（Cross Stage Paritial Network：主要从网络结构设计的角度解决推理中从计算量很大的问题）的经验，产生的Backbone结构，其中包含了5个CSP模块，CSP模块前面的卷积核的大小都是3×3，步长为2，实现下采样。

在这里插入图片描述

Backbone有5个CSP模块，输入图像是608*608，所以特征图变化的规律是：608->304->152->76->38->19，经过5次CSP模块后得到19*19大小的特征图。
CSPNet的作者认为推理计算过高的问题是由于网络优化中的梯度信息重复导致的。采用CSP模块先将基础层的特征映射划分为两部分，然后通过跨阶段层次结构将它们合并，在减少了计算量的同时可以保证准确率。主要有三个方面的优点：
优点一：增强CNN的学习能力，使得在轻量化的同时保持准确性。
优点二：降低计算瓶颈
优点三：降低内存成本

2.3 Neck

Yolov和Yolov4都采用FPN+PAN的结构，Yolov5刚出时只使用了FPN结构，后面增加了PAN结构。

在这里插入图片描述

Yolov5和Yolov4的不同点在于，Yolov4的Neck采用的都是普通的卷积操作，Yolov5的Neck结构采用借鉴CSPNet设计的CSP2结构，加强网络特征融合的能力。

在这里插入图片描述

2.4 输出端

2.4.1 Bounding box损失函数

v4采用CIOU_Loss做Bounding box的损失函数，YOLOv5 采用了BECLogits 损失函数计算objectness score的损失，class probability score采用了交叉熵损失函数(BCEclsloss)，bounding box采用了GIOU Loss，Objectness损失函数使用GIOU。

在这里插入图片描述

补充学习：回归损失函数（未学习）

目标检测任务的损失函数一般由Classificition Loss（分类损失函数）和Bounding Box Regeression Loss（回归损失函数）两部分构成。Bounding Box Regeression的Loss近些年的发展过程是：Smooth L1 Loss-> IoU Loss（2016）-> GIoU Loss（2019）-> DIoU Loss（2020）->CIoU Loss（2020）

先综合的看下各个Loss函数的不同点：
IOU_Loss：主要考虑检测框和目标框重叠面积。
GIOU_Loss：在IOU的基础上，解决边界框不重合时的问题。
DIOU_Loss：在IOU和GIOU的基础上，考虑边界框中心点距离的信息。
CIOU_Loss：在DIOU的基础上，考虑边界框宽高比的尺度信息。

a. IOU_loss

在这里插入图片描述
可以看到IOU的loss其实很简单，主要是交集/并集，但其实也存在两个问题。问题1：即状态1的情况，当预测框和目标框不相交时，IOU=0，无法反应两个框距离的远近，此时损失函数不可导，IOU_Loss无法优化两个框不相交的情况。
问题2：即状态2和状态3的情况，当两个预测框大小相同，两个IOU也相同，IOU_Loss无法区分两者相交情况的不同。因此2019年出现了GIOU_Loss来进行改进。

b. GIOU_loss

先计算两个框的最小闭包区域面积 [公式] (通俗理解：同时包含了预测框和真实框的最小框的面积)，再计算出IoU，再计算闭包区域中不属于两个框的区域占闭包区域的比重，最后用IoU减去这个比重得到GIoU。

在这里插入图片描述

用图片来进行理解就是：

两个框的最小闭包区域面积 = 红色矩形面积
IoU = 黄色框和蓝色框的交集 / 并集
闭包区域中不属于两个框的区域占闭包区域的比重 = 蓝色面积 / 红色矩阵面积
GIoU = IoU - 比重

可以看到右图GIOU_Loss中，增加了相交尺度的衡量方式，缓解了单纯IOU_Loss时的尴尬。
但为什么仅仅说缓解呢？因为还存在一种不足：在这里插入图片描述

问题：状态1、2、3都是预测框在目标框内部且预测框大小一致的情况，这时预测框和目标框的差集都是相同的，因此这三种状态的GIOU值也都是相同的，这时GIOU退化成了IOU，无法区分相对位置关系。基于这个问题，2020年的AAAI又提出了DIOU_Loss。

附上GIoU的计算代码

def Giou(rec1,rec2):
    #分别是第一个矩形左右上下的坐标
    x1,x2,y1,y2 = rec1 
    x3,x4,y3,y4 = rec2
    iou = Iou(rec1,rec2)
    area_C = (max(x1,x2,x3,x4)-min(x1,x2,x3,x4))*(max(y1,y2,y3,y4)-min(y1,y2,y3,y4))
    area_1 = (x2-x1)*(y1-y2)
    area_2 = (x4-x3)*(y3-y4)
    sum_area = area_1 + area_2

    w1 = x2 - x1   #第一个矩形的宽
    w2 = x4 - x3   #第二个矩形的宽
    h1 = y1 - y2
    h2 = y3 - y4
    W = min(x1,x2,x3,x4)+w1+w2-max(x1,x2,x3,x4)    #交叉部分的宽
    H = min(y1,y2,y3,y4)+h1+h2-max(y1,y2,y3,y4)    #交叉部分的高
    Area = W*H    #交叉的面积
    add_area = sum_area - Area    #两矩形并集的面积

    end_area = (area_C - add_area)/area_C    #闭包区域中不属于两个框的区域占闭包区域的比重
    giou = iou - end_area
    return giou

c. DIOU_loss

好的目标框回归函数应该考虑三个重要几何因素：重叠面积、中心点距离，长宽比。
针对IOU和GIOU存在的问题，作者从两个方面进行考虑
一：如何最小化预测框和目标框之间的归一化距离？
二：如何在预测框和目标框重叠时，回归的更准确？
针对第一个问题，提出了DIOU_Loss（Distance_IOU_Loss）在这里插入图片描述

DIOU_Loss考虑了重叠面积和中心点距离，当目标框包裹预测框的时候，直接度量2个框的距离，因此DIOU_Loss收敛的更快。像前面好的目标框回归函数所说的，这时并没有考虑到长宽比。在这里插入图片描述

问题：比如上面三种状态，目标框包裹预测框，本来DIOU_Loss可以起作用。
但预测框的中心点的位置都是一样的，因此按照DIOU_Loss的计算公式，三者的值都是相同的。
针对这个问题，又提出了CIOU_Loss，不对不说，科学总是在解决问题中，不断进步！！

d. CIOU_loss

CIOU_Loss和DIOU_Loss前面的公式都是一样的，不过在此基础上还增加了一个影响因子，将预测框和目标框的长宽比都考虑了进去。在这里插入图片描述

v是衡量长宽比一致性的参数：在这里插入图片描述

这样CIOU_Loss就将目标框回归函数应该考虑三个重要几何因素：重叠面积、中心点距离，长宽比全都考虑进去了。

2.4.2 nms非极大值抑制

在目标检测的后处理过程中，针对很多目标框的筛选，通常需要nms操作。Yolov4在DIOU_Loss的基础上采用DIOU_nms的方式，而Yolov5中仍然采用加权nms的方式。
在这里插入图片描述

采用DIOU_nms，中间箭头的黄色部分，原本被遮挡的摩托车也可以检出。

在同样的参数情况下将nms中IOU修改成DIOU_nms，对于一些遮挡重叠的目标，确实会有一些改进。虽然大多数状态下效果差不多，但在不增加计算成本的情况下，有稍微的改进也是好的。在这里插入图片描述
比如黄色箭头部分原本两个人重叠部分，IOU_nms修改成DIOU_nms，可以将两个目标检出。

3.Yolov5四种网络结构的不同点

3.1 四种结构的参数

v5四个文件的内容基本上都一样，只有最上方的depth_multiple和width_multiple两个参数不同：（1）Yolov5s.yaml 在这里插入图片描述

（2）Yolov5m.yaml 在这里插入图片描述

（3）Yolov5l.yaml 在这里插入图片描述

（4）Yolov5x.yaml 在这里插入图片描述

通过参数depth_multiple控制网络的深度，width_multiple控制网络的宽度。

3.2 Yolov5网络结构

将Backbone部分提取出来理解如何控制网络的宽度和深度，yaml文件中的Head也是同样的原理。

在这里插入图片描述

yolo.py中下方这一行代码将四种结构的depth_multiple，width_multiple赋值给gd，gw。

在这里插入图片描述

3.3 Yolov5四种网络的深度

3.3.1 不同网络的深度

CSP1结构应用于Backbone中，CSP2结构应用于Neck中，四种网络结构中CSP结构深度都不同。
（1）以Yolov5s为例，第一个CSP1使用了1个残差组件所以是CSP1_1。Yolov5m中增加了网络深度，第一个CSP1使用了2个残差组件，是CSP1_2。Yolov5l中使用了3个残差组件。Yolov5x中使用了4个残差组件。其余的第二个CSP1和第三个CSP1也是同样的原理。
（2）在第二种CSP2结构中也是同样的方式，以第一个CSP2结构为例。
Yolov5s组件中使用了2×X=2×1=2个卷积，因为Ｘ=1，所以使用了1组卷积，因此是CSP2_1。Yolov5m中使用了2组，Yolov5l中使用了3组，Yolov5x中使用了4组。其他的四个CSP2结构也是同理。Yolov5中，网络的不断加深，也在不断增加网络特征提取和特征融合的能力。

3.3.2 控制深度的代码

控制四种网络结构的核心代码是yolo.py中下面的代码，存在两个变量n和gd。将n和gd带入计算，看每种网络的变化结果。

在这里插入图片描述

3.3.3 验证控制深度的有效性

选择最小的yolov5s.yaml和yolov5l.yaml两个网络结构将gd(height_multiple)系数代入看是否正确。

在这里插入图片描述

a. yolov5s.yaml
depth_multiple=0.33，即gd=0.33，而n则由上面红色框中的信息获得。
以上面网络框图中的第一个CSP1为例，即上面的第一个红色框。n等于第二个数值3。
而gd=0.33，带入3.3.2中的计算代码，n=1。第一个CSP1结构内只有1个残差组件，即CSP1_1。
第二个CSP1结构中，n等于第二个数值9，而gd=0.33，带入3.3.2中计算，n=3，因此第二个CSP1结构中有3个残差组件，即CSP1_3。
b. yolov5l.xml
depth_multiple=1，即gd=1，与上面的计算方式相同，第一个CSP1结构中，n=3，带入代码中，结果n=3，因此为CSP1_3。

3.4 Yolov5四种网络的宽度

3.4.1 不同网络的宽度

如上图表格中所示，四种Yolov5结构在不同阶段的卷积核的数量都是不一样的，因此也直接影响卷积后特征图的第三维度（厚度），这里表示为网络的宽度。卷积核的数量越多，特征图的厚度，即宽度越宽，网络提取特征的学习能力也越强。
（1）以Yolov5s结构为例，第一个Focus结构中最后卷积操作时，卷积核的数量是32个，经过Focus结构特征图的大小变成304×304×32。Yolov5m的Focus结构中的卷积操作使用了48个卷积核，因此Focus结构后的特征图变成304×304×48。Yolov5l，Yolov5x也是同样的原理。
（2）第二个卷积操作时，Yolov5s使用了64个卷积核，因此得到的特征图是152×152×64。而Yolov5m使用96个特征图，因此得到的特征图是152×152×96。Yolov5l，Yolov5x也是同理。
（3）后面三个卷积下采样操作也是同理，四种不同结构的卷积核数量不同，直接影响网络中比如CSP1、CSP2等结构，各个普通卷积操作时的卷积核数量也同步调整，影响整体网络的计算量。将结构图和前面第一部分四个网络的特征图链接，对应查看，思路会更加清晰。（未做）

3.4.2 控制宽度的代码

在Yolov5的代码中，控制宽度的核心代码是yolo.py文件里面的这一行：

在这里插入图片描述

它所调用的子函数make_divisible的功能是：在这里插入图片描述

3.4.3 验证控制宽度的有效性

选择最小的Yolov5s和中间的Yolov5l两个网络结构，将width_multiple系数带入，看是否正确。

在这里插入图片描述

a. yolov5s.yaml中width_multiple=0.5，即gw=0.5。在这里插入图片描述

以第一个卷积下采样为例，即Focus结构中下面的卷积操作。Backbone的信息，Focus中标准的c2=64，而gw=0.5，代入3.4.2中的计算公式，结果=32，Yolov5s的Focus结构中，卷积下采样操作的卷积核数量为32个，第二个卷积下采样操作标准c2的值=128，gw=0.5，代入3.4.2中结果=64。

b. yolov5l.yaml中width_multiple=1，即gw=1，而标准的c2=64，代入上面3.4.2的计算公式中，可以得到Yolov5l的Focus结构中，卷积下采样操作的卷积核的数量为64个，而第二个卷积下采样的卷积核数量是128个。另外的三个卷积下采样操作及Yolov5m，Yolov5x结构也是同样的计算方式。

4.YOLOv5相关基础概念通俗解释

4.1 IoU

IoU(Intersection over Union)，即交并比，是目标检测中常见的评价标准，主要是衡量模型生成的bounding box和ground truth box之间的重叠程度，计算公式为：

4.2 Baseline

基线(Baseline)：被用为对比模型表现参考点的简单模型。基线帮助模型开发者量化模型在特定问题上的预期表现。

4.3 GT box

ground truth红色的框是使用selective search提取出的region proposal，绿色的框是ground truth。

4.4 Precision

true positives / (true positives + false positives)

Precision就是检测出来的框的数目（或者是面积吧），除以一共画出来的框。比如说有时候你预测出来10个框，只有5个是正确的，那Precision就是5/10 = 50%。这个只是简单的比喻，可能里面会有细节上的错误。

4.5 Recall

true positives/(true positives + false negatives)

Recall就是预测出来的正确的框，除以正确的框再加上没有预测出来的ground truth的框。距离来说就是，假设你有10个类别，你预测了6个框，6个框全中了，但是还有4个没框的，这时候Recall就是6/10=60%

4.6 mAP@0.5

mAP@0.5：mean Average Precision （给每一类分别计算AP 然后做mean平均）

那AP是什么呢，之前我一直以为是Average Precision，没错，就是平均精确度，可是这个怎么定义呢？AP是Precision-Recall Curve(PRC)下面的面积！！！

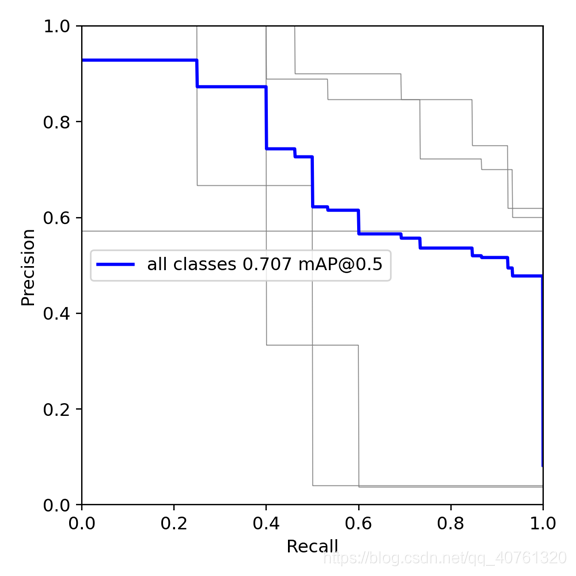
PRC怎么看：先看平滑不平滑（蓝线明显好些），在看谁上谁下（同一测试集上），一般来说，上面的比下面的好

4.7 mAP@0.5:0.95

mAP@0.5:0.95 是在不同 IoU (从 0.5 到 0.95, 步长0.05) 设置下的平均值,又可写作mmAP或 AP。

4.8 可视化结果解释

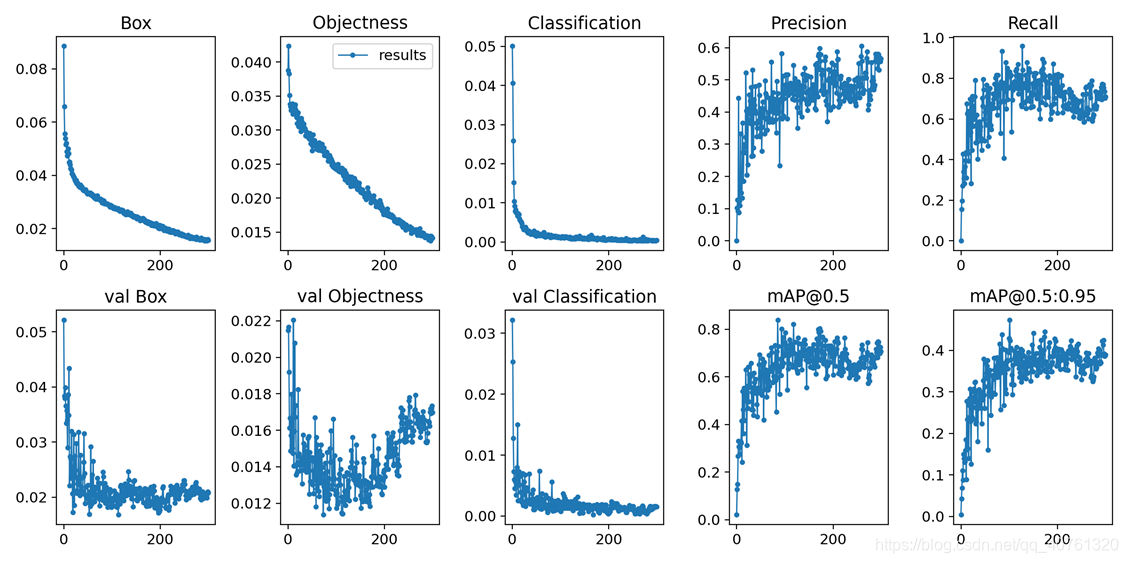
Box:推测为Box损失函数均值，越小边界盒岳精准
Objectness：推测为目标检测loss均值，越小目标检测越准；
Classification：推测为分类loss均值，越小分类越准；
Precision：准确率（找对的/找到的）；
Recall：召回率（找对的/该找对的）；
mAP@0.5 & mAP@0.5:0.95：m表示平均，@后面的数表示判定iou为正负样本的阈值，@0.5:0.95表示阈值取0.5:0.05:0.95后取均值。