计算复杂性前三章——图灵机等基础知识

一、有穷自动机

\quad 有穷自动机是能力和资源极其有限的计算机模型。描述一个自动机需要知道它一共有哪些状态，状态之间如何转换(状态之间发生转化的条件就是有新的输入字母)，它的起始状态和接受状态是什么，如下图所示：

\quad 有穷自动机是一个5元组$(Q,\sum ,\delta ,q_0,F)$，其中

• 1.$Q$是一个有穷集合，称为状态集
• 2.$\sum$是一个有穷集合，称为字母表
• 3.$\delta :Q\ast \sum ->Q$
• 4.$q_0\in Q$是起始状态
• 5.$F\subseteq Q$是接受状态集合
  
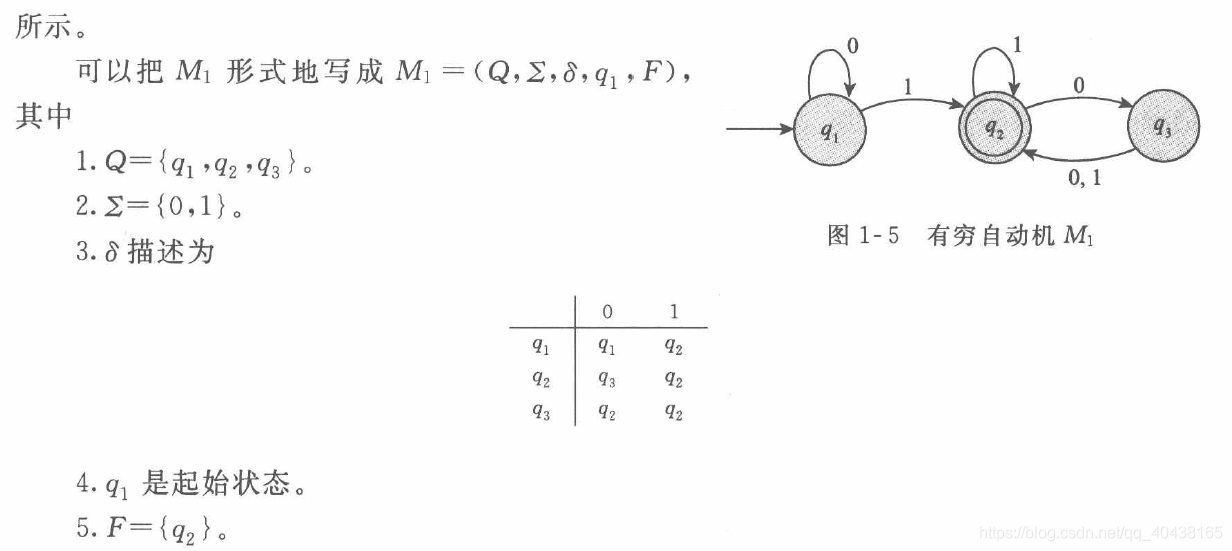
  \quad 若A是机器M接受的全部字符串集，则称A是机器M的语言，记作$L(M)=A$，又称M识别A或M接受A。一个机器可能接受若干个字符串，但它永远只能识别一个语言。在截图所示例子中，令 A = { w ∣ w 至 少 含 有 1 个 1 并 且 在 最 后 的 1 后 面 有 偶 数 个 0 } A=\{w|w至少含有1个1并且在最后的1后面有偶数个0\} A={w∣w至少含有1个1并且在最后的1后面有偶数个0}，那么，$L(M_1)=A$，M1识别A。
  \quad 如果一个语言被一台有穷自动机识别，则称它是正则语言。

二、非确定性有穷自动机

\quad 确定型有穷自动机(DFA)和非确定型有穷自动机(NFA)的异同：

• 1.DFA中当给定当前状态和输入符号时，可以确定下一个状态是什么；NFA不行
• 2.NFA是DFA的推广，因此DFA也是NFA
• 3.如下图所示，$N1$在$q_1$状态下读入1时，可能有两种选择$q_1和q_2$，即NFA中每一个状态对于字母表中每一个符号可能有多个射出的箭头，而在DFA中有且仅有一个
• 4.如下图所示，在DFA中，转移箭头上的标号是取自字母表的符号，而NFA的箭头不受此限制，可以为其他符号$ϵ$
  
  
  \quad 上图中，$N1$识别$010110$，只要有一个状态$q_4$被接受即接受。

\quad 有穷自动机是一个5元组$(Q,\sum ,\delta ,q_0,F)$，其中

• 1.$Q$是一个有穷集合，称为状态集
• 2.$\sum$是一个有穷集合，称为字母表
• 3.$\delta :Q\ast {\sum }_{ϵ}->Q$
• 4.$q_0\in Q$是起始状态
• 5.$F\subseteq Q$是接受状态集合

NFA与DFA的等价性

\quad 定义：如果两个机器识别同样的语言，则它们是等价的。DFA与NFA识别相同的语言类，因此，每一台NFA都等价于某一台DFA。
\quad 推论：一个语言是正则的，当且仅当有一台NFA识别它。
\quad 正则语言在并运算，连接运算，星号运算下封闭(借助NFA可证明)。

二、下推自动机

\quad 有穷自动机只能识别正则语言，因为它的状态集有限，存储资源有限。诸如 B = { o n 1 n ∣ n ≥ 0 } B=\{o^n1^n|n\geq 0\} B={on1n∣n≥0}这样的语言就无法识别。因为识别B需要记住它在输入中读入了多少个0，由于0的个数没有限制，因此机器不得不记住无穷多个可能，但是有穷个状态不可能做到这一点。
\quad 上述中B语言称为上下文无关文法，该语法给定一些列规则：比如语法中动词、名词、介词及它们的短语之间的关系。这类语言状态数目无限，因此识别这种语言需要在有穷自动机基础上加入存储空间，下推自动机应运而生。
\quad 下推自动机(PDA)很像NFA，但它有一个栈的额外设备。下推自动机在能力上与上下文无关文法等价，举个例子，使用下推自动机识别B语言：

\quad 下推自动机是一个6元组$(Q,\sum ,\Gamma ,\delta ,q_0,F)$，这里$(Q,\sum ,\Gamma ,F)$都是有穷集合，并且

• 1.$Q$是状态集
• 2.$\sum$是输入字母表
• 3.$\Gamma$是栈字母表
• 4.$\delta :Q\ast {\sum }_{ϵ}\ast {\Gamma }_{ϵ}->P(Q\ast {\Gamma }_{ϵ})$
• 5.$q_0\in Q$是起始状态
• 6.$F\subseteq Q$是接受状态集合

三、图灵机

\quad 某些语言即不是正则的，也不是上下文无关的，称为非上下文无关语言，例如语言 B = { a n b n c n ∣ n ≥ 0 } B=\{a^nb^nc^n|n\geq 0\} B={anbncn∣n≥0}。目前的模型还不能识别这类语言，因此不能作为计算机的通用模型。
\quad 图灵机功能则更加强大，图灵机与有穷自动机类似，但它有无限大容量的存储且可以任意访问内部数据。图灵机是一种更加精确的通用计算机模型，能模拟实际计算机的所有计算行为。当然也有图灵机不能解的问题，这类问题已经超出了计算理论的极限。图灵机组成如下：

图灵机的形式化定义

\quad 图灵机的核心在于转移函数 δ : Q ∗ Γ − > Q ∗ Γ ∗ { L , R } \delta:Q*\Gamma->Q*\Gamma*\{L,R\} δ:Q∗Γ−>Q∗Γ∗{L,R}，举个例子：若当前机器处于状态$q$，读写头所在方格内包含符号$a$，则当$\delta (q,a)=(r,b,L)$时，机器写下b以代替a，并进入状态r。第三个分量L或R指出在写带之后，读写头向左L还是向右R。
\quad 图灵机是一个6元组$(Q,\sum ,\Gamma ,\delta ,q_0,q_{accept},q_{reject})$，这里$(Q,\sum ,\Gamma )$都是有穷集合，并且

• 1.$Q$是状态集
• 2.$\sum$是输入字母表，不包含特殊符号$空格$
• 3.$\Gamma$是带子字母表，其中空格和$\sum \in \Gamma$
• 4. δ : Q ∗ Γ − > Q ∗ Γ ∗ { L , R } \delta:Q*\Gamma->Q*\Gamma*\{L,R\} δ:Q∗Γ−>Q∗Γ∗{L,R}是转移函数
• 5.$q_0\in Q$是起始状态
• 6.$q_{accept}\subseteq Q$是接受状态
• 7.$q_{reject}\subseteq Q$是拒绝状态，且$q_{accept}\ne q_{reject}$

\quad 图灵可识别语言：在输入上运行一个图灵机，可能出现三种结果：接受、拒绝或循环，这里循环仅仅指机器不停机！！！
\quad 图灵可判定语言：对所有的输入都停机，永不循环。如果某个语言能被某一图灵机判定，则称它是图灵可判定的。

图灵机的变形

\quad 多带图灵机：有多个带子，其余与普通图灵机完全一样。每个多带图灵机等价于某一个单带图灵机(只需证明它们能相互模拟即可，把多带上内容拼接在一起用一个带子模拟即可)。
\quad 非确定型图灵机： δ : Q ∗ Γ − > P ( Q ∗ Γ ∗ { L , R } ) \delta:Q*\Gamma->P(Q*\Gamma*\{L,R\}) δ:Q∗Γ−>P(Q∗Γ∗{L,R})，机器在多种可能性动作中选择一种继续。每个非确定图灵机都等价于某一个确定型图灵机。

枚举器

\quad 枚举器是图灵机的一种变形，枚举器是带有打印机的图灵机。枚举器以空白输入的工作带开始运行，不停机会打印出串的一个无限序列。枚举器所枚举的语言是最终打印出的串的集合。
\quad 定理：一个语言是图灵可识别的，当且仅当存在枚举器枚举它。