for my article

1. basic

1. $h(u)=\frac{1}{2}\Vert u-\beta {\Vert }_2^2+\lambda \Vert u{\Vert }_1$ is strictly convex,

we need to prove $S_{\lambda }(\beta )={\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{x}}_{\lambda \Vert \cdot {\Vert }_1}$

$f:{\mathbf{R}}^N\to \mathbf{R}$
$y$ is a subgradient of $f$ at $x_0$, if $f(x)\ge f(x_0)+⟨y,x-x_0⟩$ for all $x\in {\mathbf{R}}^N$, and $y\in \partial f(x_0)$

$0\in u-\beta +\partial (\lambda \Vert u{\Vert }_1)$, the i-th component $u_i$ obeys $u_i={\beta }_i-\partial (\lambda |u_i|)$. Then $u_i=\max (|{\beta }_i|-\lambda ,0)\cdot \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}({\beta }_i)={\mathcal{P}}_{\lambda }({\beta }_i)$
Thus, we have $S_{\lambda }(\beta )={\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{x}}_{\lambda \Vert \cdot {\Vert }_1}\beta$ by the concept of the soft-thresholding operator.

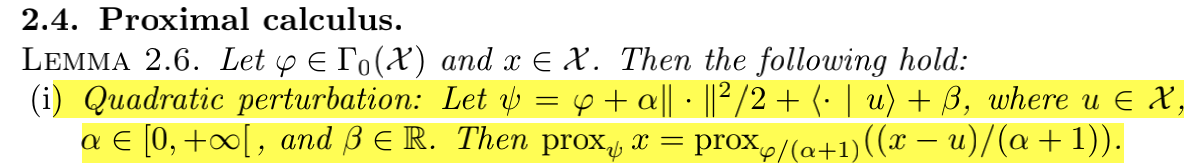
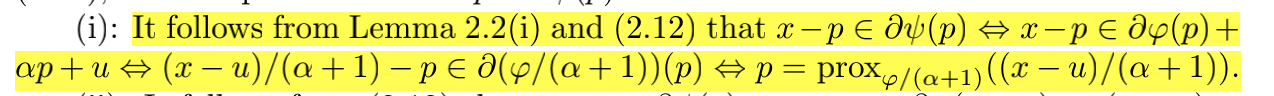
2. The proof of Lemma2

$p(\beta )=\lambda \gamma \Vert \beta {\Vert }_1$ tell us that ${\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{x}}_p\beta =S_{\lambda \gamma }(\beta )$.

$\lambda p_{\gamma ,\epsilon }(\beta )=p(\beta )+\lambda \epsilon \Vert \beta {\Vert }_2^2$, and then we have ${\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{x}}_{\lambda p_{\gamma ,\epsilon }}\beta ={\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{x}}_{\frac{p}{1+p}}(\frac{\beta -u}{1+\rho })$, where $\rho =2\lambda \epsilon ,u=0,\sigma =0,$ Therefore,
$$\begin{array}{rl}{\mathrm{p}\mathrm{r}\mathrm{o}}_{\lambda p_{\gamma ,\epsilon }}\beta & ={\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{x}}_{\frac{p}{1+2\epsilon \lambda }}(\frac{\beta }{1+2\epsilon \lambda })\\ & =S_{\frac{\lambda \gamma }{1+2\epsilon \lambda }}(\frac{\beta }{1+2\epsilon \lambda })\\ & =\frac{1}{1+2\epsilon \lambda }{S}_{\lambda \gamma }(\beta )\end{array}$$

3. for ${\ell }_{0.5}$

Since the function $h(u)=\frac{1}{2}\Vert u-\beta {\Vert }_2^2+\lambda \Vert u{\Vert }_{0.5}$ is strictly convex, it is easy to see that there exists a unique minimizer. According to the definition of the proximity operator, we need to prove
$H_{\lambda }(\beta )={\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{x}}_{\lambda \Vert \cdot {\Vert }_{0.5}}\beta$

To do this, recalling the concept of a subgradient of a convex function $f:{\mathbf{R}}^N\to \mathbf{R}$, we say that $y$ is a subgradient of $f$ at $x_0$, if $f(x)\ge f(x_0)+⟨y,x-x_0⟩$ for all $x\in {\mathbf{R}}^N$, denoted by $y\in \partial f(x_0)$. Now $u$ minimizes $h$ if and only if $0$ is a subgradient of the functional $h$ at point $u$, that is, $0\in u-\beta +\partial (\lambda \Vert u{\Vert }_{0.5})$, i.e. the the $i$-th component $u_i$ obeys $u_i={\beta }_i-\partial (\lambda |u_i{|}_{0.5})$. Then $这里根据徐宗本老师的证明写出结果$ = ${\mathcal{P}}_{\lambda }({\beta }_i)$.Thus, we have $H_{\lambda }(\beta )={\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{x}}_{\lambda \Vert \cdot {\Vert }_{0.5}}\beta$ by the theorem of the hard-thresholding operator. This completes the proof.
$$\begin{array}{rl}{\mathrm{p}\mathrm{r}\mathrm{o}}_{\lambda p_{\gamma ,\epsilon }}\beta & ={\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{x}}_{\frac{p}{1+2\epsilon \lambda }}(\frac{\beta }{1+2\epsilon \lambda })\\ & =H_{\frac{\lambda \gamma }{1+2\epsilon \lambda }}(\frac{\beta }{1+2\epsilon \lambda })\end{array}$$