密码学 (cryptography I - Dan Boneh)【一】Introduction

学习课程：斯坦福大学密码学公开课
课件和作业(附答案)链接：https://pan.baidu.com/s/1vogTE2Flpzi9DmoclLPGQw
提取码：1mrp

Course Overview

这是一个典型的加密会话场景
no eavesdropping: 攻击者不能窃听消息，或者即使窃听了也无法获取其中内容
no tampering：攻击者不能篡改消息

加密会话场景中最重要的两个部分就是：握手协议（协商会话使用的对称密钥）、加密传输（用协商好的密钥进行传输）。协商的过程中通常会涉及到非对称加密算法。

对硬盘文件的加密保护在哲学意义上，和会话加密保护是一样的。在会话场景中，Alice是发送了一个信息给Bob；而在硬盘文件加密中，是这个时间的Alice把文件发送给了下一个时间的Alice。因此也有no eavesdropping和no tampering的要求。

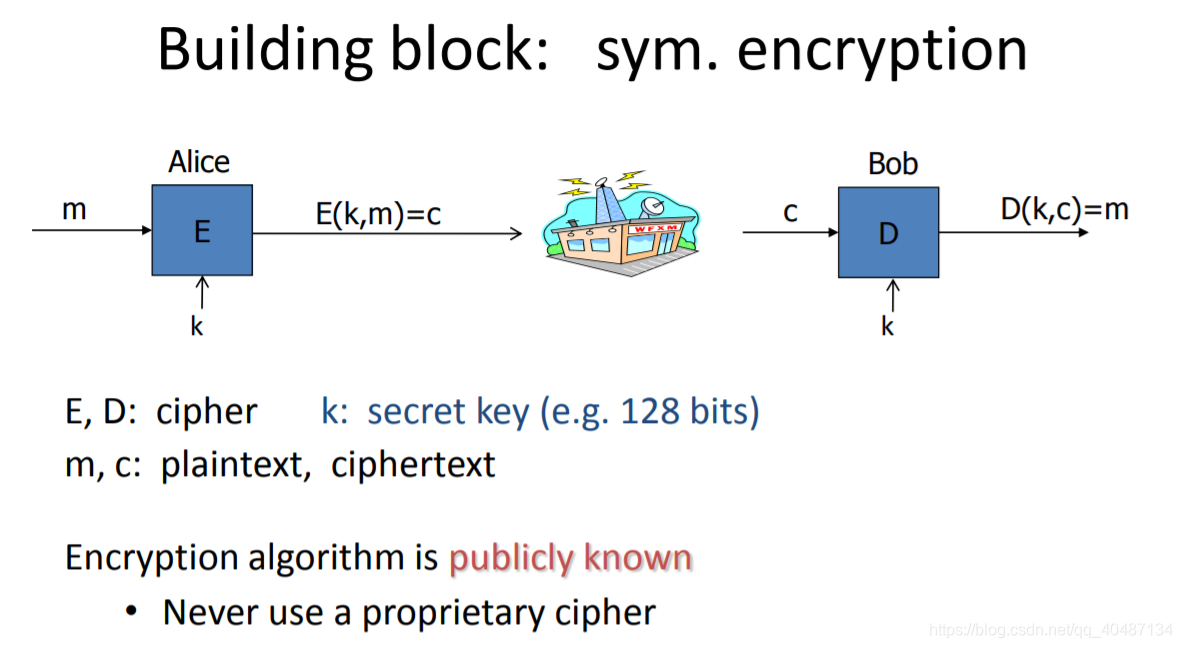
分组是对称加密的典型特点。明文被分组后被同一个密钥k进行对称加密。
很重要的一点是，对称加密算法的安全性不在于加密算法的保密性。事实上，对称加密算法应该是公开的，只有密钥k是保密的。

密钥的不同使用场景。有一个密钥只加密一个文件的，也有一个密钥加密多个文件的。

What is cryptography?

加密会话：Alice和Bob先协商共享密钥k，接着使用k来进行安全的加密会话。
Alice和Bob协商用于communication的对称加密密钥。在此过程中，Alice和Bob还需要确定对方的身份，即：Alice确定和自己协商的是Bob而不是其他人，Bob也一样。attacker即使监听了该会话，也无法解析出协商的k。
使用共享密钥进行会话。attacker通过监听无法获取会话信息。attacker一旦篡改了会话信息也会被及时发现。即加密机制提供了confidentiality保密性和integrity完整性。

Digital signatures：数字签名
在传统场景中的签名，可能不同文件上的签名都是一致的，比如你的名字。
但在数字签名中，不同文件上的签名往往不一致，因为如果一直的话，别人就可能复制你的签名到你不想签名的文件上，来伪造签名。
数字签名通常是待签内容的一个函数值，伪造者应该不能复制出签名，因为不同文件的函数值不一样。

Anonymous communication：匿名通讯
Alice想和Bob通信，经过一系列的代理，Bob不知道和他通信的人是谁，代理们也不知道Alice在和Bob通信。这个过程中有加密和解密。尽管Bob不知道Alice是谁，但仍然可以回应她，也就是通信是双向的。

Anonymous digital cash：匿名数字货币
Alice想用一美元的数字货币，以匿名的方式来买一本书。因为是匿名的，Alice有可能无限地重复使用手中的一美元货币。如何在匿名的情况下阻止这一事件发生，又如何在Alice重复花费手中的虚拟货币后能追究她的责任。
在技术层面上解决这一问题的思路是，当Alice正常使用手中的一美元货币时，是匿名的，一旦她花费了第二次，她的身份就会暴露。

Elections：选举
如何知道选举的胜出者，但不知道每个voter的投票结果。
引入election center选举中心，投票的结果会以加密的形式发送给选举中心，选举中心可以算出选举的最终结果。但除了能计算出选举结果外，选举中心无法知道其他信息。当然，选举中心还要判断这个voter是否有资格投票，或者限定每个voter只能投一次。

Private auctions：私密拍卖
假设拍卖使用的规则是Vickery：中标者是出价最高的人，中标者支付的钱是竞价金额中第二高的价钱。
如何在不知道每个竞拍者的身份和报价的情况下，计算出中标的人是谁，以及他该付的金额。即在此过程中，除了中标者和其应该付的价格，其他信息均不能被透露给任何人，即使是拍卖中心也不知道。

上图两种应用场景的更一般表述为
secure multi-party computation：安全多方计算
参与者有一秘密信息需要输入，如投票结果、拍卖价格。我们通常会想到用一个可信的第三方trusted authority来帮助我们计算结果。虽然这样可以实现我们的需求，但是在这个过程中，必须保证第三方是可信的，这就存在安全隐患。
但是在密码学中有这样的定理：如果一件事能依靠可信第三方解决，那么它一定可以不依靠可信第三方解决。
具体来说，参与者们互相直接规定一个协议。基于该协议，参与者们互相交流，交换信息。最后的结果就在交换信息的过程中被计算出来。并且在交换信息的过程中，没有任何多余的信息被泄漏。

privately outsourcing computation：私有外包计算
Alice有一个发送给Google的搜索请求。Alice可以通过一种特殊的机制把搜索请求加密，Google服务器接受的请求后，不需要解密就可以进行搜索运算。Google搜索返回的结果也是密文的形式，Google会把密文结果返回给Alice，完成本次搜索。在这整个过程中，Google并不知道Alice搜索了什么，也不知道Alice得到了什么。

zero knowledge：零知识证明
在一个大素数分解的场景中，p、q是两个大素数，N是两个素数的乘积。通过pq计算N是很容易的，但是通过N来分解出pq是极其困难的。Alice知道pqN，而Bob只知道N。
零知识证明：Alice可以向Bob证明自己知道N的分解，即知道pq，但是却不用告诉Bob pq的值。也就是Bob完全不知道pq的值，但却可以确信Alice知道它们。
另一个例子：Alice解决了一个数独问题，并向Bob证明了自己已经解决了这个问题。Bob可以验证Alice的确解决了这个问题，但却不知道Alice是怎么解决它的。

密码学是一个严谨的（rigorous）科学，在密码学中描述一个概念一般要遵循这三步（以数字签名为例）：
precisely specify threat model：精确地定义威胁模型
攻击者会如何攻击数字签名；攻击者的意图何在。定义签名不可伪造的含义
propose a construction：提出架构
攻击者可以用他掌握的方法来攻击
prove that breaking construction under threat mode will solve an underlying hard problem：证明在威胁模式下破坏该架构需要解决一个非常困难的问题（保证了安全）

History of cryptography

推荐书籍

对称加密的简单过程

历史中的对称加密
substitution cipher：替换密码
加解密需要依靠替换表

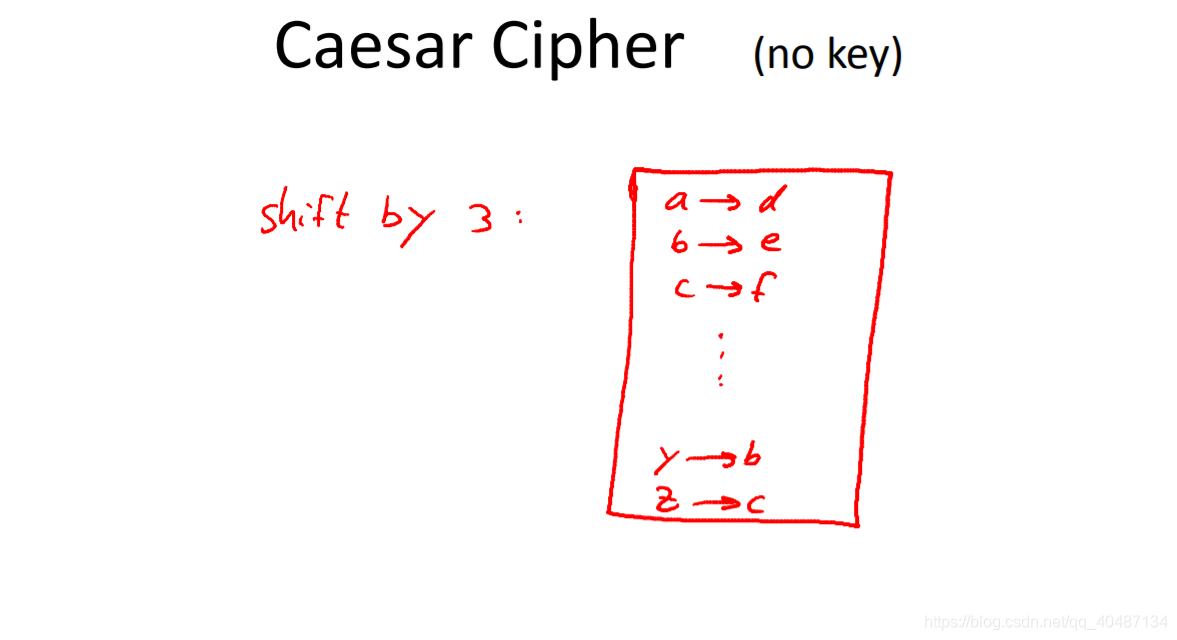
caesar cipher：凯撒密码
Dan Boneh认为凯撒密码不算加密，因为没有密钥k。
但有一种说法，把凯撒密码归类为移位密码，移位位数就是k。在凯撒密码中，k=3。

替换密码的密钥空间（密钥有多少种选择）是26!。就密钥空间的大小来说，显然这个算法是安全的。但事实并非如此，替换密码并不安全。

使用频率攻击法是很容易攻破替换密码的。


简单的频率分析，就是通过不同字母在英语文献中出现的频率猜出替换表。

维吉尼亚密码。就是用一串字符作为密钥k，反复使用对明文进行加密。
破解维吉尼亚密码也十分简单。
首先要算出密钥k的长度。这里有两种方法可以行得通：Kasiski测试法和重合指数法。

Kasiski测试法：
1.在密文中标出重复的三个或多个字符结构；
2.对每一个字符结构，记下结构的起始位置；
3.计算相邻的起始点的距离；
4.对每个距离求出所有因数；
5.密钥的长度为步骤4中出现的某一因数
一般来说，密文越长，越准确。

重合指数法（科学高效）
重合指数的定义
一个字母串X中随机取出两个字母，这两个字母恰好相同的概率记为I_c(X)
对于完全随机的字母串 I_c(X)=0.038
对于英文文本 I_c(X)=0.065
单表代换密码中，密文的重合指数和明文相同

重合指数最接近0.065时，对应的m应该就是密钥k的长度。确定密钥字长度后，可以使用频率分析方法分别解密
Y₁, Y₂, …, Y_m即当猜对密钥k时，算出的值最接近0.065

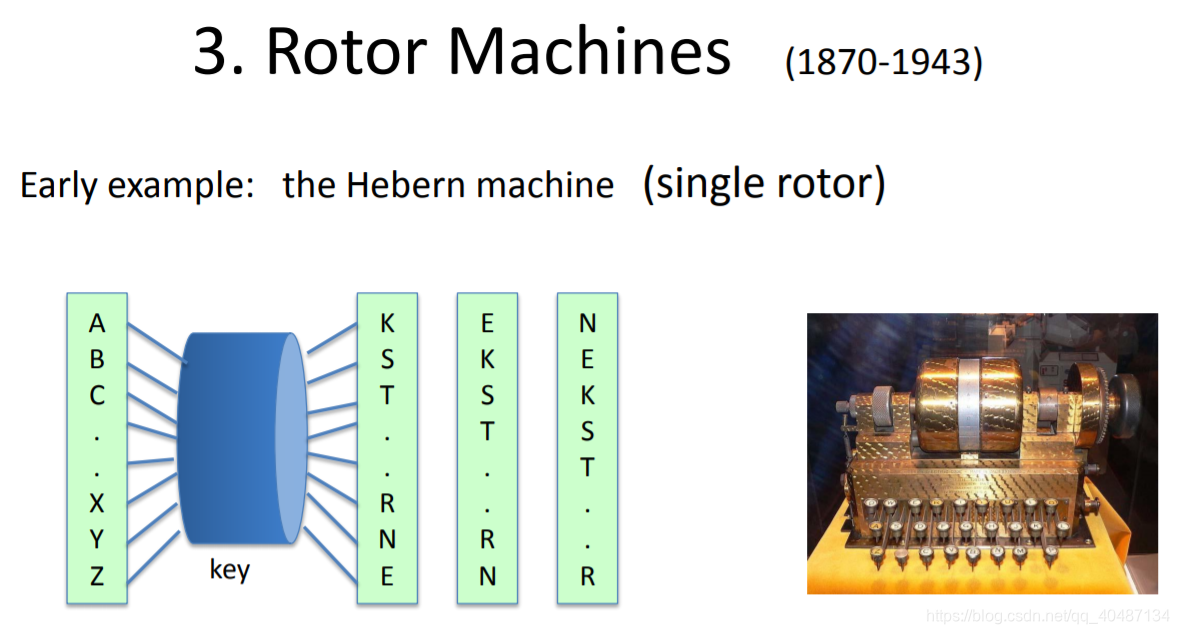
维吉尼亚密码的加强版，密钥就是碟片。每输入一个字符，碟片就会转一下。通过频率分析也能破解，只要获得的密文数量够多。

再次加强，但还是被破解了。。。

简单知道，以后细谈。

Discrete Probability

详细的可以去看http://en.wikibooks.org/High_School_Mathematics_Extensions/Discrete_Probability

简单的概率分布小知识。

集合的一些小知识。
概率不等式




随机算法。
deterministic algorithm：相同的输入会有相同的输出
randomized algorithm：在输入时添加一个随机数，随机数也会参加运算。这会使相同的输入有着不同的输出，因为每次随机数都不一样。



异或XOR在密码学中为何如此重要。
Y是一个随机变量，X是均匀分布的随机变量，Z=Y异或X，那么Z也是均匀分布的随机变量。这一性质在密码学中十分重要。
假设Y只有一位，这一定理便很容易证明。如上图所示。


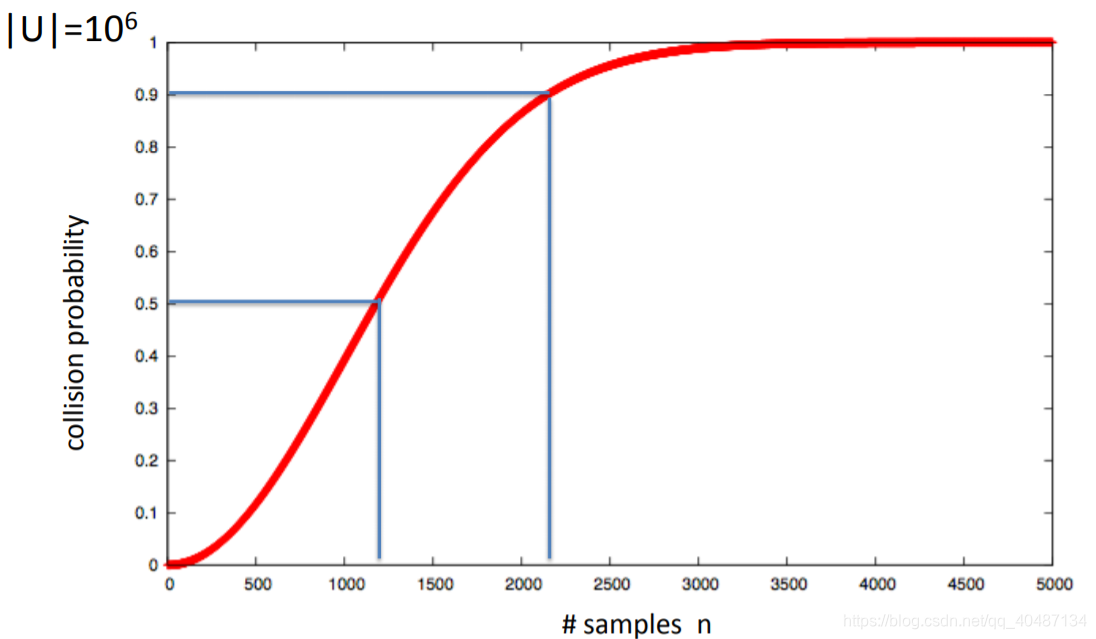
生日悖论，都知道。一个很大的集合在选取了较少样本的情况下就很有可能发生碰撞。

：）