【CCF 201909-5】城市规划(LCA+暴力全排列40 & 树形dp100) Apare_xzc

城市规划(ccf 201909-5)

---

题面：

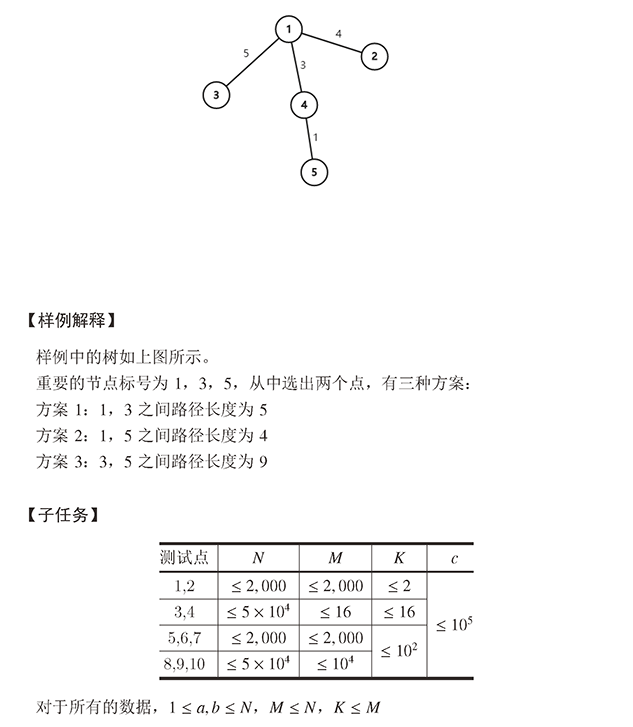
思路

1. 我一看求树上的距离，就想到了很喜欢的LCA, 可以O(1)求距离，然后又看m个节点选K个，一看，我能不能暴力dfs出C(m,k)的全排列呢？计算一下复杂度，发现前4个测试点可以过掉，于是先开心地写一发巨长的暴力（大的数据sort瞎搞的，没骗到分）

LCA + dfs暴力枚举点

//用户名   试题名称	提交时间	    代码长度	  编程语言	评测结果	得分	时间使用	空间使用
//<许智超> 城市规划	11-22 10:59	3.180KB	  C0X	    错误	40	    3.078s	15.37MB
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+100;
const int maxm = 2e5+100;
int head[maxn],tot;
struct Node{
   
	int to,Next,d;
}node[maxm];
void initEdge()
{
   
	tot = 0; 
	memset(head,-1,sizeof(head));
}
void addedge(int from,int to,int d)
{
   
	node[tot].to = to;
	node[tot].d = d;
	node[tot].Next = head[from];
	head[from] = tot++;
}
int good[100500];
int First[maxn],cnt;
int dfn[maxn*2];
int deep[maxn*2];
int father[maxn];
int disToRoot[maxn];
int idd[maxn]; ///是干啥用的？ 
bool vis[maxn];
bool cmp(int x,int y)
{
   
	return disToRoot[x]<disToRoot[y];
}
void dfs(int x,int dep)
{
   
	vis[x] = true;
	dfn[++cnt] = x;
	deep[cnt] = dep;
	First[x] = cnt;
	for(int i=head[x];i!=-1;i=node[i].Next)
	{
   
		int to = node[i].to;
		int d = node[i].d;
		if(vis[to]) continue;
		father[to] = x;
		disToRoot[to] = disToRoot[x]+d; 
		dfs(to,dep+1);
		dfn[++cnt] = x;
		deep[cnt] = dep;	
	}	
}
int ST[maxn][20];
int Log2[maxn]={
   -1};
void preRMQ(int m)
{