玩转图论算法（4）图的深度优先遍历（检测无向图的环）【Java实现】

最新推荐文章于 2025-03-03 20:35:52 发布

蜘蛛侠不会飞

最新推荐文章于 2025-03-03 20:35:52 发布

阅读量1.9k

点赞数 1

分类专栏：数据结构文章标签：图论算法 bfs dfs 数据结构

本文链接：https://blog.csdn.net/qq_40587575/article/details/105893428

版权

数据结构专栏收录该内容

14 篇文章

订阅专栏

4-9 无向图的环检测

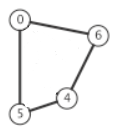
如果在遍历的过程中，发现某个顶点有一条边指向已经访问过的顶点，且这个已访问过的顶点不是当前顶点的父节点（这里的父节点表示DFS遍历顺序中的父节点），则说明图包含环。

如图中：从0开始DFS（深度优先遍历），0->6->4->5，此时顶点5的一条边指向顶点0，顶点0已经访问过，但却不是顶点5的父节点（顶点4），说明出现了环。

package graphDFS;

import java.util.ArrayList;

// 无向图的环的检测问题

public class CycleDetection {
	
	// 创建一个数组，
	private ArrayList<Integer> res = new ArrayList<>();  // 输出最后深度优先遍历的结果
	private boolean[] visited;
	private boolean hasCycle = false;
	
	private Graph graph;
	public CycleDetection(Graph graph) {
		this.graph = graph;  
		visited = new boolean[graph.V()]; // 结点的数量
		//dfs(0);
		// 改进的地方：对每一个结点进行遍历
		for (int v = 0; v < graph.V(); v++) {
			if (!visited[v]) {
				dfs(v, v);
			}
		}
	}
	
	private void dfs(int v, int parent) {
		visited[v] = true;
		res.add(v);
		for (int w: graph.adj(v)) {  // 遍历该节点的相邻结点
			if (! visited[w])
				dfs(w, v);   // w 的 遍历的上一个结点是 v
			else if(w != parent) {   // 如果 w 已经被访问了，且不是 v 的上一个结点
				hasCycle = true;
			}
		}
		
	}
	
	public boolean hasCycle(){
		return hasCycle;
	}

	public static void main(String[] args) {
		Graph graph = new Graph("g3.txt");
		CycleDetection cycleDetection = new CycleDetection(graph);
		System.out.println(cycleDetection.hasCycle());
		
		Graph graph2 = new Graph("g4.txt");
		CycleDetection cycleDetection2 = new CycleDetection(graph2);  // 无环的无向图
		System.out.println(cycleDetection2.hasCycle());
		
	}

}

优化：不需要遍历全部的结点，如果判断有环的话，直接return ，退出遍历

package graphDFS;

import java.util.ArrayList;

// 无向图的环的检测问题

public class CycleDetection {
	
	// 创建一个数组，
	private ArrayList<Integer> res = new ArrayList<>();  // 输出最后深度优先遍历的结果
	private boolean[] visited;
	private boolean hasCycle = false;
	
	private Graph graph;
	public CycleDetection(Graph graph) {
		this.graph = graph;  
		visited = new boolean[graph.V()]; // 结点的数量
		//dfs(0);
		// 改进的地方：对每一个结点进行遍历
		for (int v = 0; v < graph.V(); v++) {
			if (!visited[v]) {
				if(dfs(v, v)) 
					hasCycle = true;
					break;
			}
		}
	}
	
	// 判断是否有环
	private boolean dfs(int v, int parent) {
		visited[v] = true;
		res.add(v);
		for (int w: graph.adj(v)) {  // 遍历该节点的相邻结点
			if (! visited[w]) {
				if (dfs(w, v)) return true;   // w 的 遍历的上一个结点是 v
			}
			else if(w != parent)    // 如果 w 已经被访问了，且不是 v 的上一个结点
				return true;
		}
		return false;
		
	}
	
	public boolean hasCycle(){
		return hasCycle;
	}

	public static void main(String[] args) {
		Graph graph = new Graph("g3.txt");
		CycleDetection cycleDetection = new CycleDetection(graph);
		System.out.println(cycleDetection.hasCycle());
		
		Graph graph2 = new Graph("g4.txt");
		CycleDetection cycleDetection2 = new CycleDetection(graph2);  // 无环的无向图
		System.out.println(cycleDetection2.hasCycle());
		
	}

}