数据结构----判断图是否有环的方法

目录

一.广度优先搜索遍历和深度优先搜索遍历

1.无向图

2.有向图

二.拓扑排序

---

一.广度优先搜索遍历和深度优先搜索遍历

在讲之前，要先直到"回路"和"回边"是两个不同的概念：

回路（环）：回路是指图中一系列顶点和边，它们形成一个闭合的路径，即路径的起点和终点是同一个顶点，并且路径中的边和顶点不重复（除了起点和终点）。

特点：回路是一个闭合的路径，表示图中的一部分顶点可以通过边相互访问，形成一个环。

回边：回边是在深度优先搜索（DFS）遍历有向图或无向图时遇到的一种边。它是从一个顶点指向其DFS树（如果图不是连通的，可以说是森林）中祖先的边。这里的“祖先”指的是在DFS过程中，先于当前顶点被访问的顶点。

特点：回边表示图中存在从某个顶点到其祖先的路径，但这并不意味着整个图是连通的或者形成了一个回路。

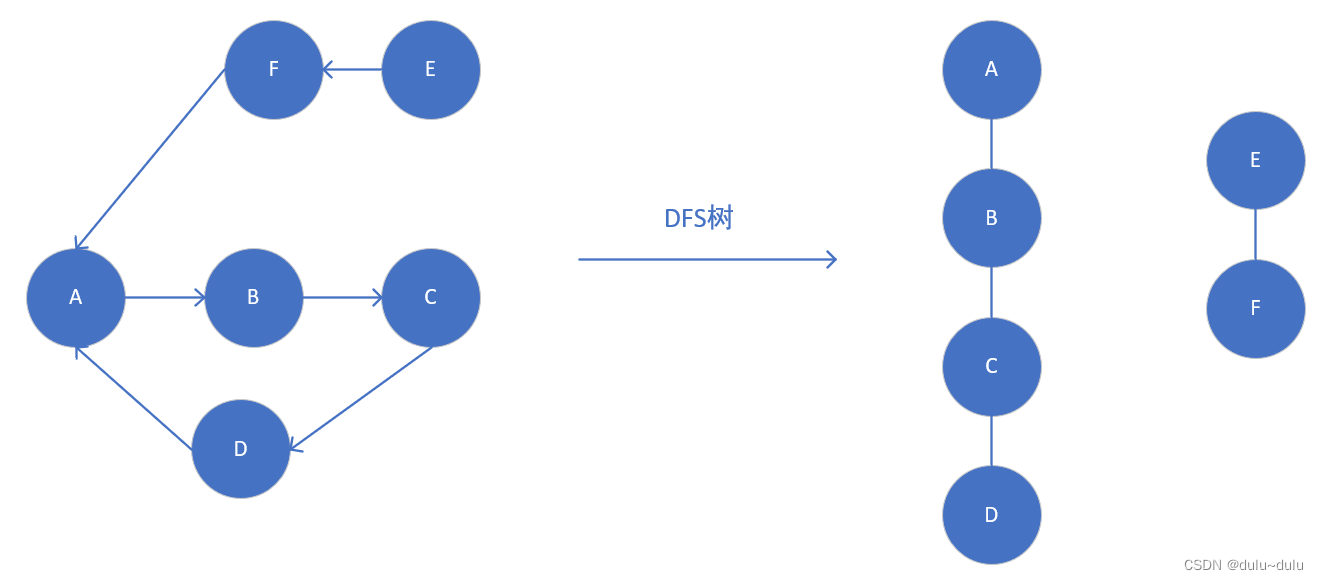
例如下图，不仅D-->A是回边，F-->A也是一条回边，如果A是F在DFS遍历中遇到的一个顶点，并且A在F之前被访问，那么A就是F在DFS树中的一个祖先，无论A是否位于与F相同的DFS树中，还是位于另一个由不同根节点开始的DFS子树中。

回归正题：

1.无向图

广度优先搜索和深度优先搜索都可能搜到已经访问的结点。

① 对于广度优先搜索遍历，假如一个无向图有环，那么在广度优先搜索的过程中，能搜到已经访问过的结点。如果一个无向图没有环（参考无向树），那么它的广度优先搜索过程是不会访问到已访问过的结点的。

② 对于深度优先搜索遍历，如果一个简单无向图有环，那么深搜的栈保存的结点形成的路径会有回边（指向栈中结点的边）。但是没有环的话，就不会出现这种情况。

2.有向图

只有深度优先搜索可以判断是否有环。

① 对于广度优先搜索遍历，无论有没有环，广度优先搜索遍历都有可能搜索到已访问过的结点：

例如下图是一个不存在回路的有向图，从顶点1开始执行广度优先遍历，若不设置访问标志位，则会重复访问顶点3。

② 对于深度优先搜索遍历，回边可能是指向深度优先森林中另一棵生成树上的顶点的弧。例如下图，F-->A是一条回边，F指向的是另一棵生成树上的顶点。

但是，从有向图的某个顶点v出发进行深度优先遍历时，若在 DFS(v)结束之前出现一条从顶点u到顶点v的回边，且u在生成树上是v的子孙，则有向图必定存在包含顶点v和顶点u的环。

例如上图，D-->A为一条回边，且D在生成树上是A的子孙，说明这个有向图存在环。

补充：这也是树和图的一大区别，树的遍历中不可能出现环，而图的遍历可能出现环。其余的区别顺带说下：

1.对于树而言，遍历的关键是找到该结点的孩子，对于图而言，则是找到与该结点相邻的结点。

2.在实现树的广度优先遍历（层序遍历）时，需要辅助队列：

① 若树非空，根结点入队。

② 若队列非空，队头元素出队并访问，同时将该元素的所有孩子入队。

③ 重复②直至队列为空。

图的广度优先遍历也用到了辅助队列：

① 找到初始顶点，并标记为被访问过。接着，让初始顶点出队，并让其相邻结点都入队。

② 若队列不空，则让队头结点出队，并让其相邻结点都入队，若被标记过以访问，那么直接跳过，将下一个未标记的结点入队。

③ 重复②直至队列为空。

3.树的深度优先搜索遍历，用到栈：从根结点出发，尽可能深地遍历树的分支，直到达到叶子结点，然后回溯到上一个结点，并继续遍历其他为访问的分支。

在图中，也用到栈：过程和树的深度遍历相同，只是中间要注意标记被访问过的结点，当遍历到标记为被访问的结点时跳过即可。

总结：由于图中可能出现环，所以要比树额外增加访问标记数组，记录某个结点是否已被访问过。

二.拓扑排序

拓扑排序用于有向无环图（DAG图）中，可以用DAG图表示一个工程，形成AOV网。忘记了可以看看：

http://t.csdnimg.cn/wk1gP

拓扑排序的过程：

① 从有向无环图中选择一个没有前驱（入度为0）的顶点并输出。

② 从网中删除该顶点和所有以它为起点的有向边。

③ 重复①和②)直到当前的AOV网为空或当前网中不存在无前驱的顶点为止。

若一个图中有回路（环），那么这个图就不能拓扑排序，例如下图，执行到第4步(红色线)时发现，当前所有顶点的入度都大于0，拓扑排序无法继续进行。

所以拓扑排序也可判断是否有环。