MATLAB图像处理——大津阈值分割（附代码）

目录

大津阈值

算法流程

流程图表示

结果

代码

---

大津阈值

        大津阈值又称最大方差阈值，是1979年由日本的大津展之提出的，它是在判别与最小二乘法原理的基础上推导出来的，其基本思想是使类间方差最大化，从而得到最优阈值。

算法流程

        令 表示一幅大小为 像素的数字图像中的 个不同的灰度级， 表示灰度级为 的像素数，图像中的像素总数为 。归一化的直方图具有分量 ，由此有

现在，假设选取一个阈值 ，并使用它把输入图像阈值化处理为两类 和 ，其中 由图像中灰度值在区间 内所有像素组成， 由灰度值在区间 内的所有像素组成。用该阈值，像素被分到类 中的概率  由如下的累计和给出：

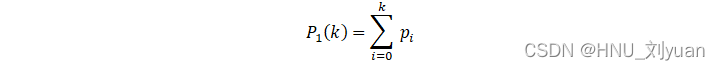
换一个角度，这是类 发生的概率。类似的，类 发生的概率为：

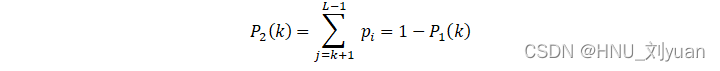
分配到类 的平均灰度值为：

类似的，分配到类 的平均灰度值为：

到第k级的累加均值（平均灰度）由下式给出：

整个图像的平均灰度由下式给出：

为了评价所选阈值分割质量，定义类间方差σ2 为：

上式可以化简为：

由上式可以看出，计算不同阈值k的类间方差 ,只需要计算m和 两个参数。为了得到最优阈值 ，从 中选择不同k计算类间方差 ，当 最大时取得的k即为最大方差阈值。

流程图表示

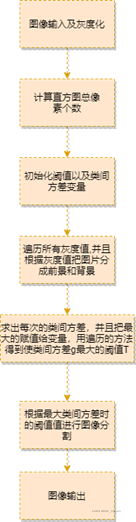
结果

         从图上可以看出，经过大津阈值分割之后基本上可以得到两个部分，可以将月球的部分从图片中提取出来。可以快速有效的找到类间分割阈值，但其缺点也很明显，就是只能针对单一目标分割，或者感兴趣的目标都属于同一灰度范围。

代码

clear; clc;
I=rgb2gray(imread('moon.jpg'));
subplot(1, 2, 1)
imshow(I);
xlabel('(a) 原始图像');
% level = graythresh(I);      %使用MATLAB 函数计算阈值
% BW = im2bw(I, level);     
% subplot(1, 3, 2)
% imshow(BW);
% xlabel('(b) graythresh');
% disp(['graythresh 计算灰度阈值:', num2str(level*255)]);
T = Otsu(double(I));     %使用大津法计算阈值
disp(['大津法计算灰度阈值:', num2str(T)])
BW = im2bw(I, T/255);
%阈值分割
subplot(1, 2, 2)
imshow(BW);
xlabel('(c) 大津法');

function ThreshValue = Otsu(Imag)
% 大津法计算阈值
% 输入：
%    Imag：二维数组，数值表示灰度；
% 输出：
%    ThreshValue：阈值
iMax = max(Imag(:));              % 最大值
iMin = min(Imag(:));               % 最小值
T = iMin:iMax;                        % 灰度值范围
Tval = zeros(size(T));               % 方差
[iRow, iCol] = size(Imag);        % 数据维度大小
imagSize = iRow*iCol;            % 像素点数量
% 遍历灰度值，计算方差
for i = 1 : length(T)
    TK = T(i);
    iFg = 0;          % 前景
    iBg = 0;          % 背景
    FgSum = 0;    % 前景总数
    BgSum = 0;    % 背景总数
    for j = 1 : iRow
        for k = 1 : iCol
            temp = Imag(j, k);
            if temp > TK
                iFg = iFg + 1;      % 前景像素点统计
                FgSum = FgSum + temp;
            else
                iBg = iBg + 1;      % 背景像素点统计
                BgSum = BgSum + temp;
            end
        end
    end
    w0 = iFg/imagSize;      % 前景比例
    w1 = iBg/imagSize;     % 背景比例
    u0 = FgSum/iFg;         % 前景灰度平均值
    u1 = BgSum/iBg;        % 背景灰度平均值
    Tval(i) = w0*w1*(u0 - u1)*(u0 - u1);     % 计算方差
end
[~, flag] = max(Tval);             % 最大值下标
ThreshValue = T(flag);
end