贝叶斯分类器

1. 贝叶斯理论

2. 连续、离散特征处理

3. 朴素贝叶斯分类器

4. 半朴素贝叶斯分类器

贝叶斯理论

在我们学习概率论课程中，基本上处处暗含着贝叶斯理论的身影。贝叶斯理论简单说可以是一种概率转化的方法，将一种较难求得的相关概率转化为几个较容易求得的概率乘积。

现在我们考虑一种分类的任务，现有N种类别，我们将类别为$c_j$的样本误分为$c_i$的损失定为${\lambda }_{ij}$,后验概率$P(c_i|x)$表示将样本x划分为$c_i$的概率。则通过上式我们可以计算出一个期望损失，也就是对整体预期损失的一个估计。又称之为为条件风险。
$R(c_i|x)={\sum }_{j=1}^N{\lambda }_{ij}P(c_j|x)$
从公式上可以理解为期望损失=单位类别判错损失*单个样本判别概率

从上述可以看出，现在的R就是我们的目标函数，代表着整个判别理论理论上的损失，那我们的目标就是最小化损失函数，也就是寻找每个样本上最合适的；类别标记使得R最小。将$h(x)$记为贝叶斯最优分类器
$h(x)=argminR(c|x)$
.现在我们以0-1损失来度量${\lambda }_{ij}$
$${\lambda }_{ij}=\{\begin{array}{rlr}1& & \text{类别预测错误}\\ 0& & \text{类别预测正确}\end{array}$$
则此时的R为：
$R(c_i|x)={\sum }_{j=1}^{N}P(c_j|x)-判对概率$
$={\sum }_{j=1}^{N}P(c_j|x)-P(c|x)$
$=1-P(c|x)$
由上述h(x)可知，最小化h(x)就等于最小化R,所以
$h(x)=argminR(c|x)=argmin(1-P(c|x))=argmaxP(c|x)$
所以，求取最佳的贝叶斯分类器就是要求的其后验概率$P(c|x)$
Bayes定理：
$P(c|x)=\frac{P(c)P(x|c)}{P(x))}$

对于给定的总样本D，单个样本P(x)对所有的类标记都一样，因此核心关注点就是分子。针对于$P(c)$我们可以采取大数定理根据样本出现的频次进行估计。但是条件概率$P(x|c)$涉及到样本的所有属性的联合概率，不易直接求得。通常我们先假定其服从某种概率分布，在基于训练样本对概率分布的参数进行估计。一般我们采用对数最大似然估计进行求解。
前提：假设服从某一分布(我们假设已知其概率密度函数)，独立同分布
假设$P(x|c)$具有确定的形式并且被参数${\theta }_c$唯一确定，$D_c$表示样本D中类别为c的样本总和

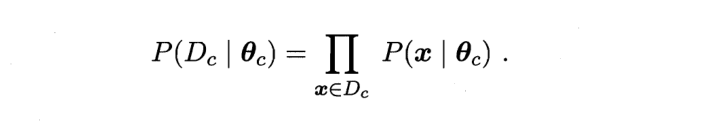
我们分别对两侧取对数，防止连乘幂次过大造成下溢

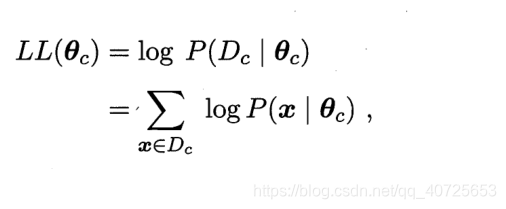
最终我们可以利用假设的概率密度分布，代入两边对θ求导计算出最终的最大似然估计值θ(高数中最大似然函数求解法)，如我们假设这里为正态分布，那么θ就指代正态分布中的$u_c,{\delta }_c^2$,计算可得：

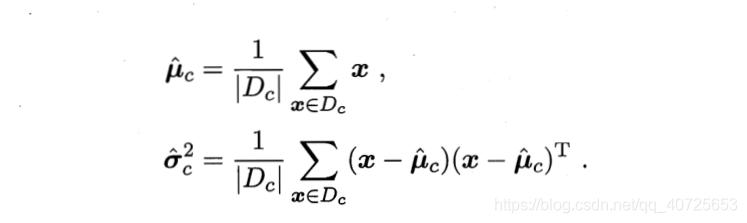
连续值、离散值处理

对于离散值来说，我们的处理方式就非常简单，只需要按照第i个属性取值为$x_i$样本的集合比上样本数即可

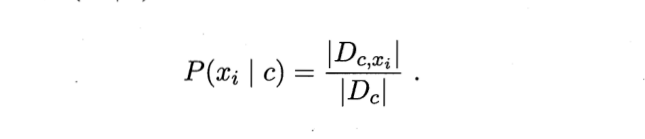
对于连续值来说，就无法这样处理了。针对于连续值我们一般有以后两种处理方法：
1：分桶法
我们将数据划分为不同的m段，为每段计算一个概率，但是这样会很受m值大小的影响
2：假设概率分布法：
我们可以假设其服从某一概率分布，然后用其概率密度分布函数就行计算，这样就把求连续数值的概率问题转变为求数值裹挟下的面积问题，如服从正态分布，我们可以这样计算：

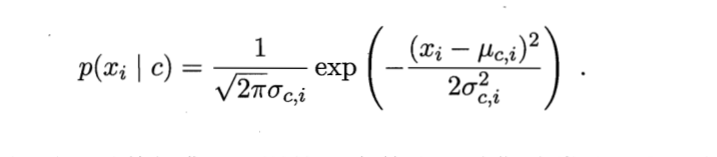
朴素贝叶斯分类器

前提：独立同分布

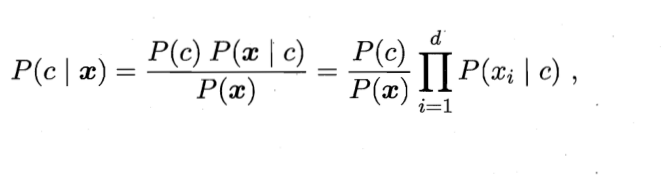
一句话总结下就是特征之间彼此毫无联系(虽然不太符合实际情况)，可以转化为单个条件特征概率连乘的形式。但是这样也会带来一个问题，一旦有一个特征未在一个类中出现过，那么其连乘的结果就为0，这样就会造成无论样本的其他属性如何变化最终都为0产生不了影响，这显然与事实不符合。"未观测到"与"出现概率为0"是两种截然不同的情况。我们为对概率进行平滑一般采取拉普拉斯修正：

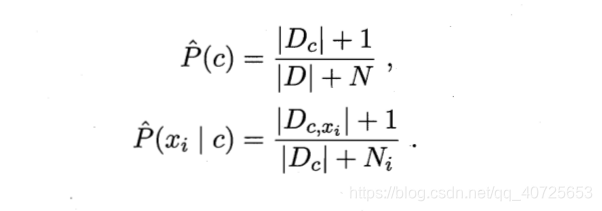
参数介绍：
Dc：样本D中类别为c的样本集合
N:D中可能的类别数
Ni:第i个属性可能的取值数
Dc,xi：Dc中第i个属性取值为xi的样本集合
+1：防止分子为0

sklearn中共为我们提供了四种贝叶斯分类函数（伯努利、补充贝叶斯、高斯、多项式），和一个贝叶斯回归函数（linear.model.BayesianRidge）

下面以一个文本分类的案例展示下高斯分布下贝叶斯分类器的效果

from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.feature_extraction.text import CountVectorizer,TfidfVectorizer
import pandas as pd
import jieba 
import numpy as np

# 获取数据
dataset = pd.read_table(r'./dataset.txt',names=['category','theme','URL','content'],encoding='utf-8')
dataset.head(-1)
# 获取文章内容
content = dataset.content.values.tolist()
# content
# 内容分词
segment_words = list()
for line in content:
    segment = jieba.lcut(line)
    if len(segment)>1 and segment!="\r\n":
        segment_words.append(segment)
segment_words[1000]

contents = pd.DataFrame({"content":segment_words})
contents = contents.content.values.tolist()
# 去除停用词表中内容
stopwords = pd.read_table(r'./stopwords.txt',quoting=3,names=["stopwords"],encoding='utf-8')
stopwords = stopwords.stopwords.values.tolist()

new_content = list()
for line in contents:
    line_content = list()
    for word in line:
        if word in stopwords:
            continue
        line_content.append(word)
    new_content.append(line_content)

df_train=pd.DataFrame({'content':new_content,'label':dataset['category']})
df_train.head()
# 类别标记离散化
label_mapping = {"汽车": 1, "财经": 2, "科技": 3, "健康": 4, "体育":5, "教育": 6,"文化": 7,"军事": 8,"娱乐": 9,"时尚": 0}
df_train.label = df_train['label'].map(label_mapping)
# 数据分割
x_train,x_test,y_train,y_test = train_test_split(df_train.content.values,df_train.label.values,test_size=0.2,random_state=100)

train_content = list()
# 训练集转化为list of str形式u，便于后续特征编码
for line_index in range(len(x_train)):
	train_content.append(' '.join(x_train[line_index]))

# 特征编码，形成一个sparse稀疏矩阵
transfer = CountVectorizer(analyzer="word",max_features=4000)
x_train = transfer.fit_transform(train_content)

# 训练模型
estimator = GaussianNB()
estimator.fit(x_train.toarray(),y_train)
# 测试集数据编码
train= list()
for index in range(len(x_test)):
    train.append(" ".join(x_test[index]))
#transfer1 = TfidfVectorizer()
transfer1 = CountVectorizer(analyzer="word",max_features=4000)
x_test = transfer1.fit_transform(train)
estimator.score(x_test.toarray(),y_test)

半朴素贝叶斯分类器

在朴素贝叶斯分类器中，我们假设的前提是独立同分布，但在现实中这一条件很难成立，特征之间或多或少都会有联系。为改善这一缺陷，半朴素贝叶斯分类器多采用独依赖估计得策略，也就是现在设计每一个属性最多依赖于一个其他属性：

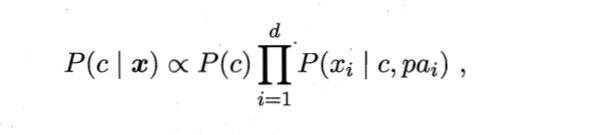
$p{a}_i$就是$x_i$所依赖的属性，我们称之为父属性(超父)。半贝叶斯分类器的方法很多，其本质思想是如何来衡量特征之间的相关性，进而提出新的计算条件概率的方法。

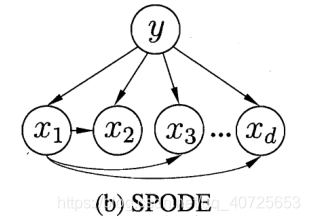
上图SPODE单一超父方法，就是假设其余特征之间彼此无关，所有的特征均与其中唯一确定的特征相关。
现今有一种基于集成学习机制更为强大的半贝叶斯分类器AODE，就是在SPODE的基础上将单一的超父变为全体超父，
也就是说现在分别都将其中一个特征进行SPODE方法，每一个特征都充当一次超父。其公式以下所示：

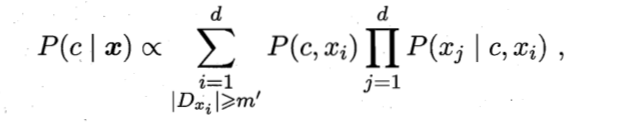
本质就是基于集成机制聚合多个SPODE模型，最终提出以下概率计算方法：

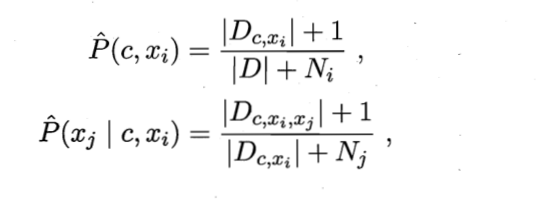
D：总样本集合
Ni:第i个属性可能的取值数
Dc,xi：Dc中第i个属性取值为xi的样本集合
Dc,xi,xj：D中类别为c且第i,j个属性取值分别为xi,xj的样本集合
+1：防止分子为0