【脉冲神经网络教程 04】脉冲神经网络搭建及训练-理论篇2

上篇讲解了如何结合Pytorch和snntorch搭建一个脉冲神经网络，并演示了前向通道运行过程。但是一个网络不经过训练是没有意义的，脉冲神经网络的训练方法有很多种，包括无监督学习的突触可塑性、有监督学习的梯度下降法。snntorch里面采用梯度下降法对脉冲神经网络进行训练。

1. 脉冲神经网络的循环结构

在之前的教程中，我们推导出LIF神经元的模型可表述为：

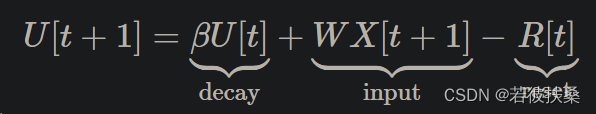
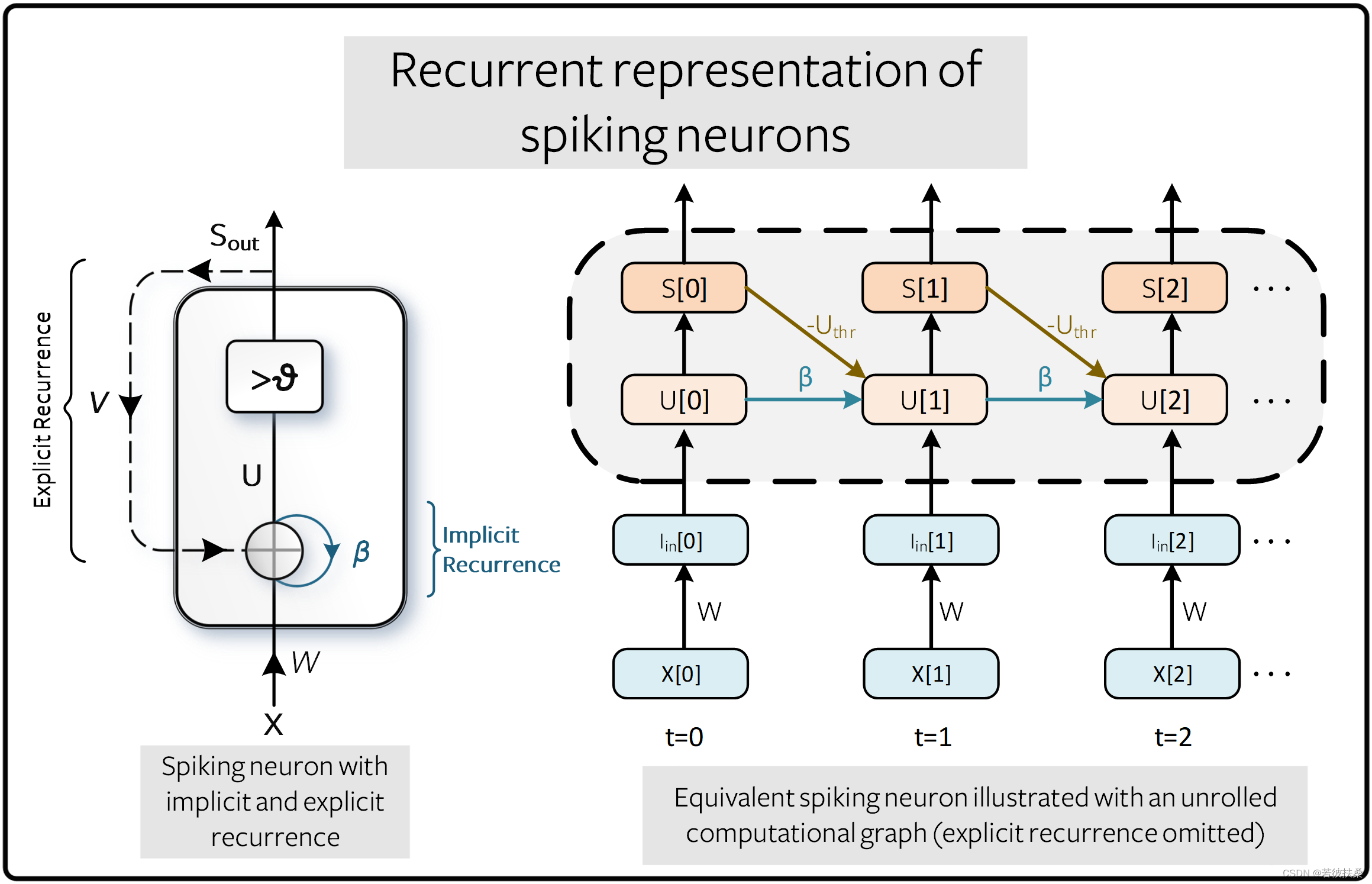
这实际上是一种类似于循环神经网络（RNN）的递归结构，这种结构更适用于处理序列数据。一个脉冲神经元的展开图如下图所示（注意这不是一个脉冲神经网络，只是一个神经元，只不过按时间展开了），横轴是模拟的时间，使用-Uthr代表复位机制，β代表连接权重，U[t]代表输入，S[t]代表输出。传统的 RNN 将 β 作为可学习参数， SNN 默认情况下将其视为超参数，使用超参数搜索取代了梯度消失和梯度爆炸问题。未来的教程将介绍如何将 β 作为可学习参数。

 对于输入U[t]，输出S[t]，复位机制-Uthr，则有

其中 Θ(⋅) 是阶跃函数： 当U[t]-Uthr大于阈值时，S[t]产生脉冲，否则静默。

2. 代梯度下降法

 我们已经得到脉冲神经元的输入U[t]和输出S[t]的关系是一个阶跃函数，此时S和U的一阶导数则为0和无穷大（在脉冲上升时刻），如下图所示。梯度下降法是利用损失相对于权重的梯度来训练网络，从而更新权重，使损失最小化。S和U的导数（梯度）为一个脉冲函数，这种情况下，要不权重不更新，要不权重就直接饱和，无法进行学习。这就是所谓的死神经元问题。

2.1 解决死神经元问题 

解决 "死神经元 "问题的最常见方法是在前向传递过程中保持阶跃函数的原样，但在后向传递时，将S与U的导数换成过程中不会扼杀学习过程的S`和U导数项 。这听起来可能有些奇怪，但事实证明，神经网络对这种近似是相当稳健的。这就是通常所说的代梯度法。snnTorch 的默认方法（截至 v0.6.0）是使用反正切函数平滑阶跃函数。使用的导数为

2.2 时间反向传播BPTT 

之前的导数等式只计算了一个时间步的梯度，但通过时间反向传播（BPTT）算法会计算从损失L到所有时间步长t的梯度，并将它们相加。权重 W应用于每个时间步长t，因此可以想象，损失L也是在每个时间步长计算的。权重对当前损失和历史损失的影响必须相加，以确定总体梯度：

举例来说，W[t-1] 对损失的影响可以写成：

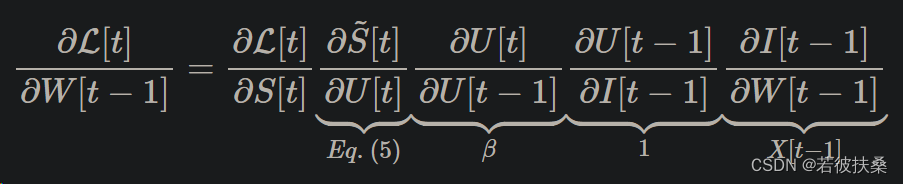
 对于单个神经元来说，时间反向传播算法如下图，这里省略了复位机制，在 snnTorch 中，复位包含在前向传递中，但从后向传递中分离出来。

 3. 设置损失及输出解码

在传统的非脉冲神经网络中，有监督的多类分类问题会选择激活度最高的神经元，并将其作为预测类别。在脉冲神经网络中，有几种解释输出脉冲的方法。最常见的方法有：