关于一个童年小游戏的一些想法

一个童年小游戏，没有正式名称，不如称为“手指碰8”。近来无事希望搞一个AI，仔细研究一下这个游戏是否存在类似五子棋的“先手必胜”之类的规则，因为它里面也为了所谓的平衡而添加了大量没有严格理论依据的规则，很像五子棋的“禁手”。

游戏过程

甲 乙 两个人各伸两只手指，如下图：

甲先手，用任意一根手指碰乙的任意一根手指，同时将两数进行 + - * /任意一种运算（本人的数只能位于运算符左侧），得到新数。如甲(1,1)选择与乙(1,1)进行加法，那么就会得到甲(2,1)：

然后乙(1,1)再与甲(2,1)重复如上操作，如果选择乘法，那么就可以得到乙(2,1)：

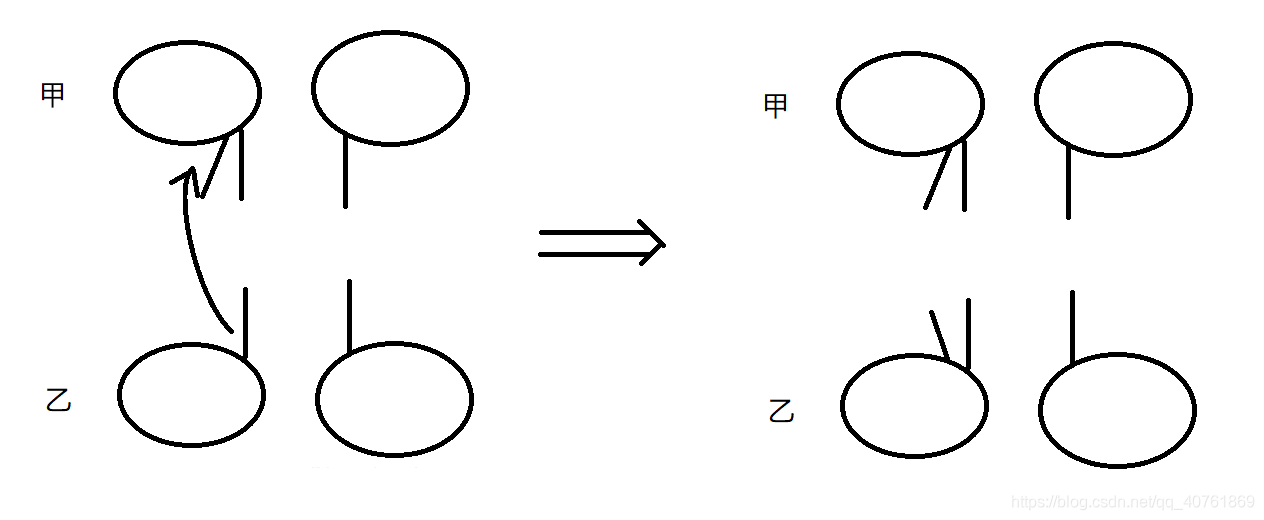
不断进行上述过程，胜利条件为某一方两根手指均为8，即若甲(8,8)，那么甲获胜。

游戏细则

1. 不可以不变，比如不能将本方数字乘以1或者加上0得到原数字；

2. 不可以双手都是0；（0将四则运算全部都限定死了，过于bug）

3. 不可以循环，否则第一个引发循环的人判负；

现阶段想法

不区分左右，使用二元组表示某一方的状态，所有状态总共有54种。我们可以将这些状态抽象成节点，从而组织成一张图。

经过简单思考即可得知，任意两个 具有一个相同数字的节点之间必然存在至少一条弧，该弧由 对方节点和四则运算的种类共同确定。

很显然，这张图虽然节点数并不多，但是弧特别多，遍历寻找解应该是不太可能了……目前还没有好的编程想法。

没想到童年一个小游戏的核心内容还真的挺复杂……