决策树基础知识

目录

1. 决策树的定义
2. 信息熵的计算
3. ID3
4. C4.5
5. CART树
6. 决策树剪枝

1. 决策树(decision tree)的定义

    决策树是一个类似于流程图的数结构：其中每个内部结点表示在一个属性上的测试，每个分支代表一个属性输出，而每个树叶结点代表类或者类分布。树的最顶层是根结点。
    决策树通常包含3个步骤：特征选择、决策树的生成、和决策树的修建

分类决策树模型是一种描述对实例进行分类的树形结构。一棵决策树包含一个根节点，若干个内部节点和若干个叶节点，叶节点对应于决策结果。

• 树的递归思想
  由根节点出发到内部结点的每一条路径构建一条规则，内部结点的特征对应着规则的条件，结点的类对应着规则的结论。
  递归结束条件：

1. 遍历完所有划分数据集的属性；
2. 每个分支下的所有实例都具有相同的分类

2. 熵(entropy)的计算

• 信息量
      一条信息的信息量大小和它的不确定性有直接的关系，要搞清楚一件非常非常不确定的事情，或者是我们一无所知的事情，需要了解大量信息>>>>信息量的度量就等于不确定性的多少。$a_i$信息的计算，已知道其概率。
  $$\mathbf{I}({\mathbf{a}}_{\mathbf{i}})=-logP(a_i)$$
• 熵
      它是表示随机变量不确定的度量，是对所有可能发生的事件产生的信息量的期望。

$$H(x)=-\sum p(x)logP(x)$$

3.联合熵
随机变量的值有多个的时候。p(x,y)表示联合概率，一起发生的概率。
$$H(X,Y)=-\sum p(x,y)logp(x,y)$$

4.条件熵/噪声熵

已知条件下，事件的不确定性的大小。X条件下Y的信息熵
$$\begin{array}{rl}H(Y|X)& =H(X,Y)-H(X)\\ & =-\sum _{x,y}p(x,y)logp(x,y)+\sum _{x}p(x)logp(x)\\ & =-\sum _{x,y}p(x,y)logp(x,y)+\sum [\sum _{y}p(x,y)]logp(x)\\ & =-\sum _{x,y}p(x,y)logp(x,y)+\sum _{x,y}p(x,y)logp(x)\\ & =-\sum _{x,y}p(x,y)log\frac{p(x,y)}{p(x)}\\ & =-\sum _{x,y}p(x,y)logp(y|x)\end{array}$$

$$\begin{array}{rl}H(X,Y)& =-\sum _{x,y}p(x,y)logp(y|x)\\ & =-\sum _x\sum _{y}p(x,y)logp(y|x)\\ & =-\sum _x\sum _{y}p(x)p(y|x)logp(y|x)\\ & =-\sum _{x}p(x)\sum _{y}p(y|x)logp(y|x)\\ & =\sum _{x}p(x)[-\sum _{y}p(y|x)logp(y|x)]\\ & =\sum _{x}p(x)H(Y|X=x)\end{array}$$

5.疑义度/损失熵

它也是条件熵，已知道Y的情况下，X的信息熵，公式证明和上面一样。
$$H(X|Y)=-\sum _{x,y}p(x,y)logp(x|y)$$

6.平均互信息

$$I(X,Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)$$
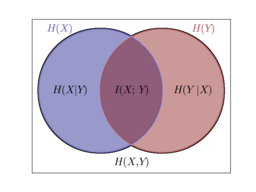
插入一张维恩图帮助理解上面各种熵的关系

7.交叉熵

    现在有关于样本集的两个概率分布 $p(x)$ 和 $q(x)$，其中 $p(x)$ 为真实分布，$q(x)$非真实分布。
$$H(p,q)=\sum _{x}p(x)log\frac{1}{q(x)}$$

3. ID3算法

• 信息增益
  "信息熵"是度量样本的不确定度，是度量样本集合纯度最常用的一种方法。
  熵的计算(2为底熵的单位是bit，e为底是纳特)：
  $$H(Y)=-\sum _{i=1}^{n}p(y_i)lo{g}_{2}p(y_i)$$
  信息增益定义
  表示得知特征A的信息而使得类X的信息的不确定性减少的程度。
  (A：代表数据集里面的特征，X：数据集里面标签的类别)
  统计学里面的公式：
  $$g(D,A)=H(D)-H(D|A)$$
  西瓜书里面的公式：
  $$Gain(D,a)=Ent(D)-\sum _{v=1}^V\frac{D^v}{D}Ent(D^v)$$
  计算的方法就是按照西瓜书里面的，信息增益就是互信息，
  计算一下使用的是统计学里面的数据
  
  类别是“是”的有9个，类别是“否”的有6个。年龄是“青年”的有5个，年龄是“中年”的有5个，年龄是“老年”的有5个。
  $$End(D)=-(\frac{9}{15}log\frac{9}{15}+\frac{6}{15}log\frac{6}{15})=0.971$$
  $D^1年龄是青年，其中“是”有2个，“否”有3个；D^2年龄是中年，其中“是”有3个，“否”有2个；D^3年龄是老年，其中“是”有4个，“否”有1个$
  $$\begin{array}{rl}Ent(D^1)& =-(\frac{2}{5}log\frac{2}{5}+\frac{3}{5}log\frac{3}{5})=0.971\\ Ent(D^2)& =-(\frac{3}{5}log\frac{3}{5}+\frac{2}{5}log\frac{2}{5})=0.971\\ Ent(D^3)& =-(\frac{4}{5}log\frac{4}{5}+\frac{1}{5}log\frac{1}{5})=0.722\end{array}$$

$$\begin{array}{rl}Gain(D,年龄)& =Ent(D)-\sum _{v=1}^3\frac{D}{D^v}Ent(D^v)\\ & =0.971-(\frac{5}{15}\times 0.971+\frac{5}{15}\times 0.971+\frac{5}{15}x\times 0.722)\\ & =0.083\end{array}$$

• ID3算法
  ID3算法的核心是在决策树各个结点上应用信息增益准则选择特征

1. ID3优点：
   理论清晰、方法简单、学习能力较强。
2. 缺点：
   1. ID3算法只有树的生成，所以该算法生成的树容易产生过拟合。
   2. 只能处理分类属性的数据，不能处理连续的数据
   3. ID3算法采用信息增益作为评价标准。信息增益的缺点是倾向于取值较多的特征，在有些情况下这类特征可能不会提供太多有价值的信息

4. C4.5

• 信息增益率
  信息增益对可取数目较多的属性有所偏好，如果将ID也作为一个特征，那么它的信息增益为0.971，因为每一个ID对应一个，即每一个对应的$Ent(D^{id})$熵为0，为了减少这种偏好带来的影响，可以使用“信息增益率”来选择最优划分的属性。
  统计学：特征A对训练数据集D的信息增益比$g_R(D,A)定义其为信息增益g(D,A)与训练数据集D的经验熵H(D)之比$
  $$g_R(D,A)=\frac{g(D,A)}{H(D)}$$
  西瓜书:
  $$Gai{n}_{r}atio(D,a)=\frac{Gain(D,a)}{IV(a)}$$
  $$IV(a)=-\sum _{v=1}^V\frac{D^v}{D}log\frac{D^v}{D}$$
• C4.5算法
  C4.5算法与ID3算法相似，C4.5使用的是信息增益比来选取特征。

1. 优点：
   • 解决偏向取值较多的属性的问题
   • 可以处理连续型属性。
2. 缺点：
   • 对数据集进行多次的顺序扫描和排序，算法的效率低。

• C4.5算法处理连续值
  • 需要连续属性离散化，最简单的策略采用二分法对连续属性进行处理，这就是C4.5算法采用的。
  • 连续值处理方法：
    给定数据集D和连续特征a，假定a出现了n个不同的值，将这n个值从小到大进行排序，取相邻的两个点的均值，作为划分点，这样的可以取n-1个划分点，计算哪个划分点的信息增益大。

5. CART

1. Gini指数

    CART(Classification and Regression Tree， 分类和回归树)决策树是使用“基尼指数”来选择划分特征属性的。数据集D的纯度可以使用Gini值来度量：

$$\begin{array}{rl}Gini(D)& =\sum _{k=1}^{|y|}\sum _{k^{\prime }\ne k}{p}_k{p}_{k^{\prime }}\\ & =\sum _{k=1}^y{p}_k(1-p_k)\\ & =1-\sum _{k=1}^{|y|}{p}_k^2\\ & =1-\sum _{k=1}^y(\frac{|C_k|}{|D|}{)}^2\end{array}$$

    $p_k$指样本属于第k类的概率，总共有y个类别，$C_k$属于第k个类别的样本子集。
    Gini(D)反映了从数据集D中随机抽取两个样本，其类别标记不一样的概率。因此，GIni(D)越小，则数据集D的纯度越高。
    属性a的基尼指数定义：
$$Gin{i}_{i}ndex(D,a)=\sum _{v=1}^V\frac{|D^v|}{|D|}Gini(D^v)$$
    选择属性，基尼指数最小的属性作为划分属性，V表示分类
例子

    计算基尼指数：
$$Gini(D,A=青年)=\frac{5}{15}(2\times \frac{2}{5}\times (1-\frac{2}{5}))+\frac{10}{15}(2\times \frac{7}{10}\times (1-\frac{7}{10}))=0.44$$

2. 回归树

    回归树使用平方误差最小准则，一个回归树对应着输入空间(特征空间)的一个划分以及在划分的单元上的输出值。假设已经将输入空间划分为M个单元$R_1$,$R_2$,$...$,$R_M$,并且在每个单元$R_m$上有一个固定的输出值$c_m$,回归树模型：
$$f(x)=\sum _{m=1}^M{c}_{m}I(x\in R_m)$$
    当输入空间的划分确定时，使用平方误差${\sum }_{x_i\in R_m}(y_i-f(x_i){)}^2$表示回归树训练数据的预测误差。
最优切分变量$j$,与切分点s，求解：

$$mi{n}_{j,s}\left[mi{n}_{c_1}\sum _{x_i\in R_1(j,s)}(y_i-c1{)}^2+mi{n}_{c_2}\sum _{x_i\in R_2(j,s)}(y_i-c2{)}^2\right]$$

    遍历变量$j$，对固定的切分变量$j$扫描切分点$s$，使得上式达到最小值的$(j,s)$

6. 决策树剪枝

    剪枝(pruning)是决策树学习算法解决过拟合的重要手段。在决策学习中，为了尽可能正确分类训练样本，结点划分过程将不断重复，有时候会出现过拟合。
决策树剪枝分为“预剪枝”(prepruning)和“后剪枝”(postpruning)。

• 预剪枝
  预剪枝是在决策树生成过程中，对每个结点在划分前进行估计，若当前节点的划分不能带来决策树泛化性能提升，则停止划分并且将当前的节点标记为叶节点。
  解决过拟合方法：
  • 树的深度
  • 叶节点树

# sklearn参数设置
from sklearn import tree
model = tree.DecisionTreeClassifier(max_depth=,   # 最大深度
									max_leaf_nodes=)  # 叶节点树

• 后剪枝
      后剪枝是先从训练集生成一棵完整的决策树，然后自底向上地对非叶节点进行考察，若该节点对应的子树替换成叶节点能带来决策树泛化性能的提示，则将该子树替换成叶节点。
  计算子树的损失函数：
  $$C_{\alpha }(T)=C(T)+\alpha |T|$$

    其中$T$为任意子树，$C(T)为对训练数据的预测误差$，$|T|$为子树的叶节点个数，$\alpha$是一个大于0的参数。$C_{\alpha }(T)$为参数是$\alpha$时的子树$T$的整体损失，$\alpha$权衡训练数据的拟合程度与模型的复杂度。