1.梯度常用符号说明
①我们常将参数上标视为某时间点,例如参数代表第0个时间点的参数,即初始参数。
②无论在哪个时间点,我们的参数都是成千上万个的,通常用下标来区分他们,例如 ,其中向量的某一元素代表了该时刻的第i个参数。
③我们常用倒三角▽L()来代表第i时刻的梯度组成的向量,其中▽L(
)=
2.学习率大小对训练的影响

①学习率过小:
损失降低过慢,容易陷入鞍点停止
②学习率过大:
当学习率大到一定程度,会导致一开始学习速度快,但逐渐变得缓慢,这就类似打高尔夫球,在即将进洞的地方依然使用比较大的力气打球,球就会一直在洞的周围徘徊。
当学习率继续增大,可能会导致损失函数直接激增,就好比打球用过力将球打的太远。
当且仅当学习率适合时,损失才会平稳降低。
3.正式由于初始设置学习率的麻烦,这才引入了自动调整学习率的各种算法
①基于epoches的学习率调整
如果我们认同一开始时参数离最优点比较远,需要大的学习率,当我们经过几轮epoches之后,离最优点变近这一假设,我们就可以使用下面这一公式进行学习率的调整:
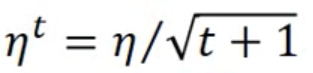
即随着t次数越多,我们更新学习率的大小就越小。
②Adagrad
方法①虽然考虑了更新次数,但是,由于不同参数有着不同的重要程度,更新时就应当有大有小,然而法①对于不同的参数,都是使用相同大小的学习率,这就会造成一定的问题。
Adagrad在①的基础之上,每个epoche更新时会去除以之前更新梯度的均方根(root mean square)
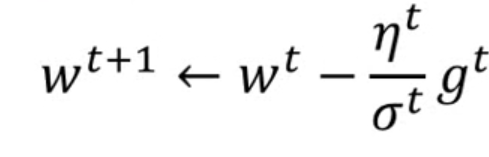
例子:

将式子简化,我们可以约去有关更新次数的信息,将adagrad简化为初始学习率除以过去更新梯度和的开根号。

对于不同dimention上的参数,根据Adagrad其梯度更新速度都是不同的,除以梯度和根号的值更类似在衡量其二次微分 。

W2取一些点的一阶导数累和后比W1的较大,和二阶导数成正比。
③RMSProp
虽然Adagrad考虑了不同dimention需要给不同学习率以达到不同更新速度的目的,但是,即使是相同dimention,在同一方向上有时也是时而陡峭时而平缓,这时就不是更新次数越多,其梯度就应该更新越慢的,真实的损失函数可能是极为复杂的。
RMSProp会综合考虑以往更新梯度和现有的梯度,并为二者赋予权重,这个权重是提前设置的超参数。

若将式子展开,会发现RMSprop实际上是在做weighted sum的RMS,前的权重为
,
④Adam
RMSProp虽然一定程度上解决了同一dimention不同时刻梯度不同的情形,但是没有解决训练卡在鞍点的问题,
Adam创新性的提出了动量Momentum的概念,我们每次移动的梯度不仅仅考虑此次更新的梯度,还要考虑之前的梯度。
参数每次更新的结果是上一时刻的动量加上梯度。
例子:


实际上,momentum也是对所有之前梯度的加权和:

从式子也可以看出,我们每次在更新参数时,一方面要考虑最新计算的梯度,另一方面也要加上一个Vi,这个值是之前所有梯度的加权和,且越靠前的梯度其权重越小。
4.特征缩放的必要性
如果不做特征缩放,不同dimention的参数对于梯度值的影响大小是不同的,当某dimention整体数值范围大过其他dimention的参数,就会导致这个dimention所连的w权重对损失的影响异常大,并且在进行梯度下降时,其损失降低的方向也并不是朝着最低点,在经过多轮更新后,可能会产生梯度消失的情况。

其中一种进行特征缩放的方法是,不同数据相同dimention的数值要减去其平均值,然后除以标准差。

这样,对于每一个dimention,我就得到了均值为0,标准差为1的正态分布,

在一个标准差范围内,即64%的概率x其值落在[-1,1]的范围内,在两个标准差范围内,也就是说95%的概率x其值落在了[-2,2]的范围内,这意味着我们的前激活值(即输入向量进行左乘矩阵并加上bias后)不会太大或太小,就不会朝着激活函数两侧偏移,远离梯度饱和区域,就会使得我们避免了梯度消失的发生。
如果feature scaling针对的是一个batch中每个hidden layer 的输入分布都固定下来,那就是所谓的Batch normalization(除此之外,BN算法为了避免修改分布导致将非线性激活近似成了线性激活后表达能力的不足,又进行了其他操作)
5.梯度下降之原理---多元泰勒展开式
在损失函数初始点处以多元泰勒展开(这里以二元为例),保留一次近似,我们有
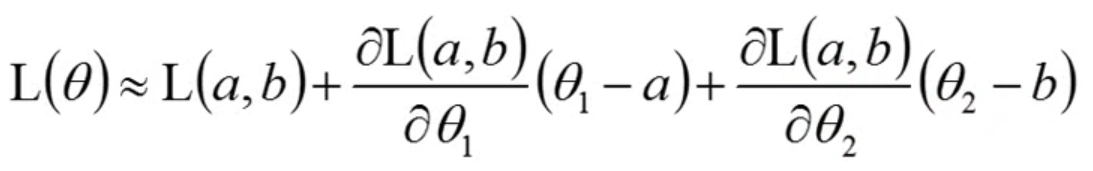
设三个常数部分分别为s,u,v
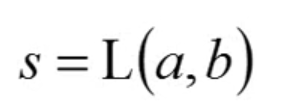
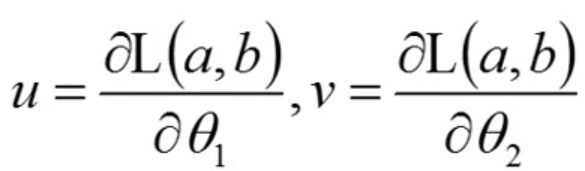
我们得
![]()
在领域内,我们有
![]()
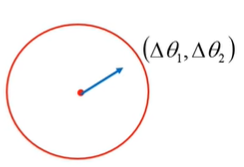
为了使得L()最小,我么需要有
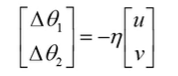
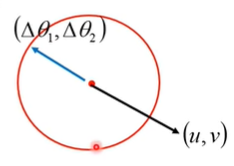
即


























 2554
2554











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








