详解最大似然估计(MLE)、最大后验概率估计(MAP),以及贝叶斯公式的理解
(1)最大似然估计
这篇文章中提到,关于最大似然估计,使用频率去估计概率,在抛硬币问题中会得到正面向上的概率是0.7的结论,其原因是由于样本数量太小,使用经验风险最小化会出现过拟合现象。
经验风险:即模型关于训练样本集的平均损失。
(2)最大后验概率估计:
为了解决过拟合问题,在抛硬币例子中加入了先验概率P(θ),最大后验概率估计得到正面向上的概率是0.558的结论,对于小样本来讲,效果更好。
下面对最大后验概率进行分析:
最大后验估计方法于是估计  为这个随机变量的后验分布的众数:
为这个随机变量的后验分布的众数:
后验分布的分母与  无关,所以在优化过程中不起作用。注意当前验
无关,所以在优化过程中不起作用。注意当前验  是常数函数时最大后验估计与最大似然估计重合。
是常数函数时最大后验估计与最大似然估计重合。
************************************************************
我们对上式使用对数损失函数时(先取负对数,再将对数展开),则上式等价于:
对比结构风险最小化公式:
由于f( | )是模型,可以是条件概率分布模型,那么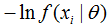
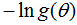
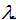
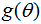
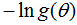
结构风险最小化就是为了在似然尽可能大的情况下避免模型太过复杂。所以得证。







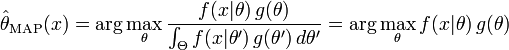
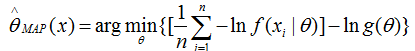
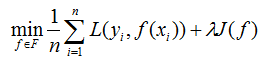














 945
945

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








