运算
常用
立 方 a 3 ± b 3 = ( a ± b ) ( a 2 ∓ a b + b 2 ) 立方a^3\pm b^3=(a\pm b)(a^2\mp ab+b^2) 立方a3±b3=(a±b)(a2∓ab+b2)
配方
a x 2 + b x + c = a ( x + b 2 a 2 + c − a ( b 2 a 2 ) ) ax^2+bx+c=a(x+\frac{b}{2a}^2+c-a(\frac{b}{2a}^2)) ax2+bx+c=a(x+2ab2+c−a(2ab2))
多项式长除法
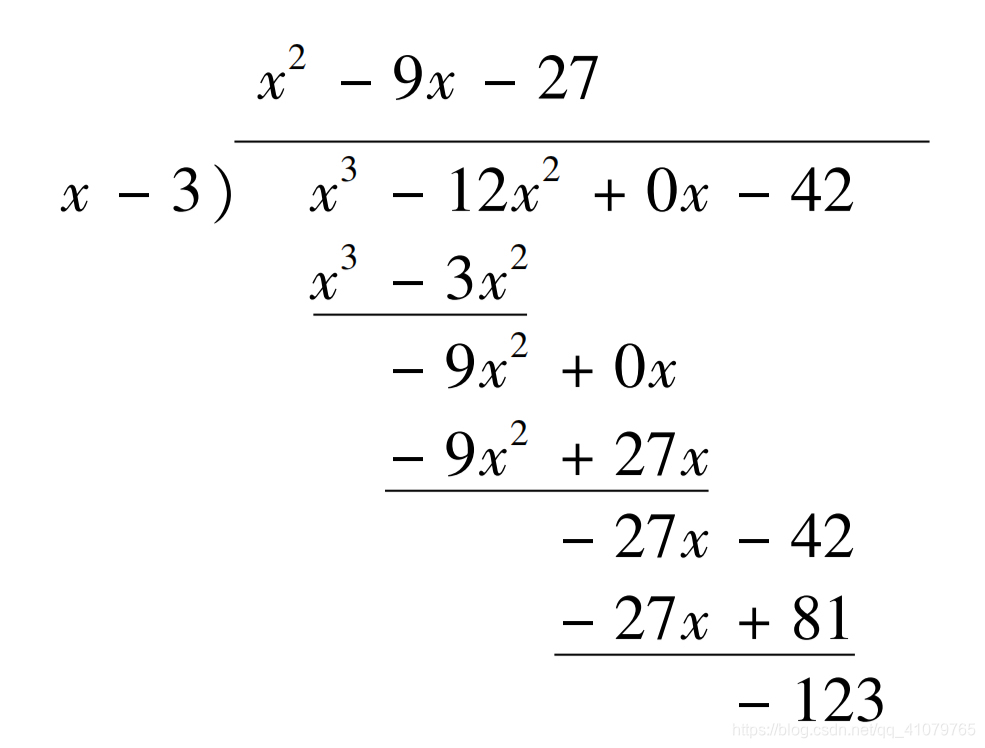
二次函数 f ( x ) = a x 2 + b x + c = 0 ( a ≠ 0 ) f(x)=ax^2+bx+c=0(a\ne 0) f(x)=ax2+bx+c=0(a=0)
常用
Δ
=
b
2
−
4
a
c
\Delta =b^2-4ac
Δ=b2−4ac
根
式
x
1
,
2
=
−
−
b
b
2
−
4
a
c
2
a
根式x_{1,2}=-\frac {-b\sqrt{b^2-4ac}}{2a}
根式x1,2=−2a−bb2−4ac
韦
达
定
理
{
x
1
+
x
2
=
−
b
a
x
1
x
2
=
c
a
韦达定理\begin {cases}x_1+x_2=-\frac{b}{a}\\ x_1x_2=\frac{c}{a}\end {cases}
韦达定理{x1+x2=−abx1x2=ac
其他
- 有 理 数 系 的 方 程 有 根 a + b 则 必 有 根 a − b 有理数系的方程有根a+\sqrt {b}则必有根 a-\sqrt{b} 有理数系的方程有根a+b则必有根a−b
- 与有理数系的方程_
a
x
2
+
b
x
+
c
=
0
(
a
≠
0
)
ax^2+bx+c=0(a\ne 0)
ax2+bx+c=0(a=0)的二根互为相反数的新方程
a
x
2
−
b
x
+
c
=
0
ax^2-bx+c=0
ax2−bx+c=0
互为倒数的新方程 c x 2 + b x + a = 0 cx^2+bx+a=0 cx2+bx+a=0
互为负倒数的新方程 c x 2 − b x + a = 0 cx^2-bx+a=0 cx2−bx+a=0 - f ( x ) = a x 2 + b x + c f(x)=ax^2+bx+c f(x)=ax2+bx+c满足 a > b > c , f ( x ) = 0 a>b>c,f(x)=0 a>b>c,f(x)=0,则 { a > 0 c < 0 a + b + c = 0 \begin{cases}a>0\\c<0\\a+b+c=0\end{cases} ⎩⎪⎨⎪⎧a>0c<0a+b+c=0
- b=0时，函数为偶函数
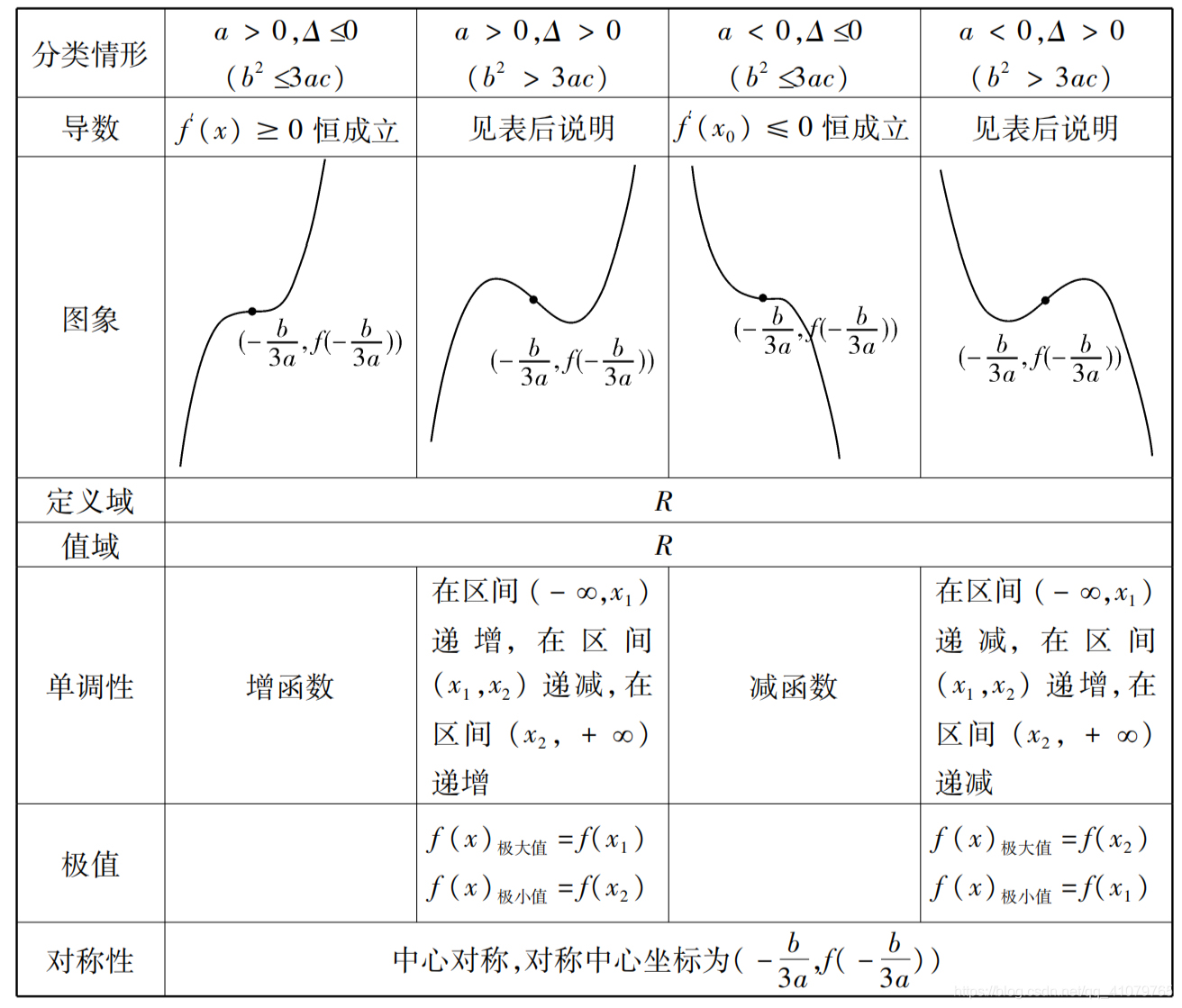
三次函数 f ( x ) = a x 2 + b x + c f(x)=ax^2+bx+c f(x)=ax2+bx+c
常用
Δ = 4 ( b 2 2 − 3 a c 2 ) \Delta =4(\frac{b}{2}^2-\frac{3ac}{2}) Δ=4(2b2−23ac)
图像
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
