1 巴斯模型概念
巴斯扩散模型针对创新产品、技术的采用和扩散,常被用作市场分析工具,对新产品、新技术需求进行预测。而新产品创新扩散是指新产品从创造研制到进入市场推广、最终使用的过程,表现为广大消费者从知晓、兴趣、评估、试用到最终采用新产品的行为。
巴斯扩散模型的许多变形也已被开发出来,用以满足某些特殊情形的精确需求。
2 创新扩散理论-Diffusion of Innovations Theory
巴斯模型的理论基础是新产品创新扩散理论。下面一张图很好地解释了创新扩散模型。

3 Bass模型详解
模型的核心思想是创新群体群体的购买决策独立于社会系统其他成员,而模仿群体购买新产品的时间受到社会系统的影响,并且这种影响随购买人数增加而增加,因为模仿群体的购买决策时间受到社会系统成员的影响。
Bass模型的基本形式:
d
N
(
t
)
d
t
=
p
[
m
−
N
(
t
)
]
+
q
N
(
t
)
m
[
m
−
N
(
t
)
]
\frac{dN(t)}{dt} = p[m - N(t)] + q\frac{N(t)}{m}[m - N(t)]
dtdN(t)=p[m−N(t)]+qmN(t)[m−N(t)]
N
(
t
)
=
m
F
(
t
)
N(t) = mF(t)
N(t)=mF(t)
其中,
- N(t) 表示在时间t 时的累计采用者,n(t) 表示t 时刻采用者的数量
- F(t) 表示在时间t 时的采用者数量占总的潜在采用者数量的概率,f(t) 表示在时间t 时的采用者数量占总的潜在采用者数量的概率密度函数
- p表示外部影响系数,q表示内部影响系数
- m表示最终采用者的总数,即市场潜力。
我们分别看柿子中的两个部分
p
[
m
−
N
(
t
)
]
p[m - N(t)]
p[m−N(t)]
这一部分表示因为外部影响而购买新产品的采用人数,即这些采用者不受那些已经采用该种新产品的人的影响,成为创新采用者。
q
N
(
t
)
m
[
m
−
N
(
t
)
]
q\frac{N(t)}{m}[m - N(t)]
qmN(t)[m−N(t)]
这一部分表示那些受先前购买者影响而购买的采用人数。当t = 0时,
n
(
0
)
=
p
m
n(0) = pm
n(0)=pm
即假设在创新扩散开始时,有pm个采用者,也可以理解为新产品引入市场前的试销或赠送的样品。
上面这一个微分方程解出来的结果为:
N
(
t
)
=
m
1
−
e
−
(
p
+
q
)
t
1
+
(
q
p
)
e
−
(
p
+
q
)
t
N(t) = m\cfrac{1 - e^{-(p+q)t}} {1 + (\cfrac{q}{p})e^{-(p+q)t}}
N(t)=m1+(pq)e−(p+q)t1−e−(p+q)t
n
(
t
)
=
m
p
(
p
+
q
)
2
e
−
(
p
+
q
)
t
[
p
+
q
e
−
(
p
+
q
)
t
]
2
n(t) = m\cfrac{p(p +q)^2e^{-(p+q)t}} {[p + qe^{-(p+q)t}]^2}
n(t)=m[p+qe−(p+q)t]2p(p+q)2e−(p+q)t
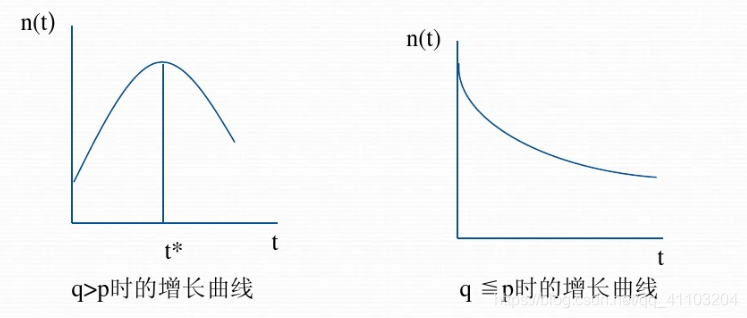
如果Bass模型的创新系数p与模仿系数q的参数值上分析,如果q>p,则采纳曲线由最高点,即此产品的扩散是成功的;如果q<=p,则增长曲线没有极值点,随时间呈指数衰减状态,说明此产品的市场扩散失败。
3 巴斯模型的假设
- 市场潜力随时间的推移保持不变
- 一种创新的扩散独立于其他创新
- 产品性能随时间推移保持不变
- 社会系统的地域界限不随扩散过程而发生改变
- 扩散只有两个阶段过程,采用和不采用
- 一种创新的扩散不受市场营销策略的影响
- 不存在供给约束
- 采用者是无差异的、同质的;但是将消费者分为两类:创新消费者和模仿消费者。新产品的潜在采用者会受到大众媒体影响(外部影响)的采用者称为创新者;会受到口头传播影响(内部影响)的采用者为模仿者
4 应用和局限
适用范围:
- 耐用消费品的分析预测,既适用于新产品,也适用于已进入市场的产品。
- 简洁明了,适用于初次评估。
- 变形模型,可以使用与一些特殊情况。
局限:
- 巴斯模型给出的是购买者数量,而不是企业的产品销售量,但是销售量可以根据顾客使用频率间接估计。
- 虽然巴斯模型在理论上比较完善,但是只适用于已经在市场中存在一定时期的新产品的市场预测,而往往新产品上市的时候,器治疗和性能对顾客来讲相当陌生,企业无法对巴斯模型中的创新系数和模仿系数作出可靠的估计,此时就需要对巴斯扩散模型做出一定的补充。
4 代码
# 最小二乘法
from math import e # 引入自然数e
import numpy as np # 科学计算库
import matplotlib.pyplot as plt # 绘图库
from scipy.optimize import leastsq # 引入最小二乘法算法
# 样本数据(Xi,Yi),需要转换成数组(列表)形式
ti = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
yi = np.array([8, 11, 15, 19, 22, 23, 22, 19, 15, 11])
# 需要拟合的函数func :指定函数的形状,即n(t)的计算公式
def func(params, t):
m, p, q = params
fz = (p * (p + q) ** 2) * e ** (-(p + q) * t) # 分子的计算
fm = (p + q * e ** (-(p + q) * t)) ** 2 # 分母的计算
nt = m * fz / fm # nt值
return nt
# 误差函数函数:x,y都是列表:这里的x,y更上面的Xi,Yi中是一一对应的
# 一般第一个参数是需要求的参数组,另外两个是x,y
def error(params, t, y):
return func(params, t) - y
# k,b的初始值,可以任意设定, 一般需要根据具体场景确定一个初始值
p0 = [100, 0.3, 0.3]
# 把error函数中除了p0以外的参数打包到args中(使用要求)
params = leastsq(error, p0, args=(ti, yi))
params = params[0]
# 读取结果
m, p, q = params
print('m=', m)
print('p=', p)
print('q=', q)
# 有了参数后,就是计算不同t情况下的拟合值
y_hat = []
for t in ti:
y = func(params, t)
y_hat.append(y)
# 接下来我们绘制实际曲线和拟合曲线
# 由于模拟数据实在太好,两条曲线几乎重合了
fig = plt.figure()
plt.plot(yi, color='r', label='true')
plt.plot(y_hat, color='b', label='predict')
plt.title('BASS model')
plt.legend()

参考资料:
https://baike.baidu.com/item/%E5%B7%B4%E6%96%AF%E6%89%A9%E6%95%A3%E6%A8%A1%E5%9E%8B/10258655?fr=aladdin
https://www.jianshu.com/p/269b8894d630?from=timeline
https://wenku.baidu.com/view/dcc6191155270722192ef7cf.html
https://zhuanlan.zhihu.com/p/28153851
https://www.jianshu.com/p/d3eb8d1a5e8c
https://www.jianshu.com/p/269b8894d630?from=timeline
























 4349
4349

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








