【BZOJ - 4754】独特的树叶（树哈希）

最新推荐文章于 2025-02-03 16:01:44 发布

xuanweiace

最新推荐文章于 2025-02-03 16:01:44 发布

阅读量350

点赞数

分类专栏： bzoj 哈希

本文链接：https://blog.csdn.net/qq_41289920/article/details/99479512

版权

bzoj 同时被 2 个专栏收录

16 篇文章

订阅专栏

哈希

9 篇文章

订阅专栏

题干：

JYY有两棵树A和B：树A有N个点，编号为1到N；树B有N+1个点，编号为1到N+1。JYY知道树B恰好是由树A加上一个叶

节点，然后将节点的编号打乱后得到的。他想知道，这个多余的叶子到底是树B中的哪一个叶节点呢？

Input

输入一行包含一个正整数N。

接下来N-1行，描述树A，每行包含两个整数表示树A中的一条边；

接下来N行，描述树B，每行包含两个整数表示树B中的一条边。

1≤N≤10^5

Output

输出一行一个整数，表示树B中相比树A多余的那个叶子的编号。如果有多个符合要求的叶子，输出B中编号最小的

那一个的编号

Sample Input

5 1 2 2 3 1 4 1 5 1 2 2 3 3 4 4 5 3 6

Sample Output

Hint

解题报告：

哈希规则：子树u的哈希值由它的每一个子树vi的哈希值得来，首先将所有f(v)排个序（防止顺序不同造成影响），然后

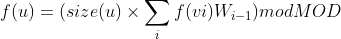$f(u)=(size(u) \times \sum_i f(vi)W_{i-1} )mod MOD$ ，

W是事先选取的一个位权，MOD是模数，size(u)是子树u的大小。

这样DFS一遍可求出以1号节点为根时，所有子树的哈希值f(u)。

但是这是无根树，我们想求出以任意节点为根时整棵树的哈希值。

设fa[u]以1为根时u的父亲，则上面的f(u)也是以fa[u]为根时子树u的哈希值。

再求一个g(u)表示以u为根时子树fa[u]的哈希值。这个g(u)怎么求呢？再DFS一遍，对于每个节点，g(u)由g(fa[u])以及u的每个兄弟vi的f(vi)得来。但是直接暴力枚举的话在菊花图上是O(n^2)的，那怎么办呢？

对于每个节点u维护一个数组，存储它所有儿子的哈希值f(v)，如果有父亲，则g(u)也在里面，把这个数组排好序，求出每个前缀的哈希值和每个后缀的哈希值。这时，以u为根时整棵树的哈希值就是整个数组的哈希值（再乘上子树大小n）。

此时求每个儿子v的g(v)，就是从那个数组中间去掉f(v)后的哈希值，二分查找后把前缀哈希值和后缀哈希值拼起来就可以得到。记得乘上v为根时uu的size即n−size(v)。

这样就求出以每个节点为根的哈希值了。

把A的所有哈希值存到一个set里，然后枚举B的每个度为1的点u，求出以u为根它的唯一子树v的哈希值，如果set里有这个值，u就是所求的点之一。部分内容参考自：链接

首先明确一个问题，以u为根节点的树的Hash值=树的大小 * 子树Hash值的带权和 % MOD，也就是说这个根节点是以子树大小的身份参与到其中的。也就是HASH[u]其实重头戏在于u的孩子节点，而u在其中的作用只是size那一部分权重而已，其他的都与他无关。这是在做树的问题的时候，和其他问题不一样的一点，也是比较有特色的一点。

g[v]代表以v为根时，子树u的Hash值。（也就是以v为根节点的部分哈希和）那么g[v]由g[u]和v的一系列兄弟节点f[vi]带权得来。

AC代码：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<queue>
#include<map>
#include<vector>
#include<set>
#include<string>
#include<cmath>
#include<cstring>
#define F first
#define S second
#define ll long long
#define pb push_back
#define pm make_pair
using namespace std;
typedef pair<int,int> PII;
const int MAX = 2e5 + 5;
const ll MOD = 2000020331;
//const ll MOD = 2000004199;  用这个模数都没有问题！
const ll seed = 31;//
ll PW[MAX];
struct Edge {
	int v,ne;
} e[MAX];
int head[MAX],tot;
int n;
int deg[MAX];
bool isB;
void add(int u,int v) {
	if(isB) deg[u]++;
	e[++tot].v = v;
	e[tot].ne = head[u]; head[u] = tot;
}
int size[MAX],fa[MAX];
vector<ll> son[MAX],sl[MAX],sr[MAX];
ll f[MAX],g[MAX];
set<ll> vis;
ll dfs1(int cur,int rt) {
	ll res = 0;
	fa[cur] = rt; son[cur].clear();//必须要清空！！ 
	size[cur] = 1;
	for(int i = head[cur]; ~i; i = e[i].ne) {
		int v = e[i].v; if(v == rt) continue;
		ll tmp = dfs1(v,cur);
		son[cur].push_back(tmp);
		size[cur] += size[v]; 
	}
	if(son[cur].empty()) return f[cur] = 1;//注意叶子结点的HASH值需要是1，而不能是0，也就是son数组中必须都是正数的HASH值。
	sort(son[cur].begin(),son[cur].end());
	int up = son[cur].size();
	for(int i = 0; i<up; i++) res = (res * seed + son[cur][i]) % MOD;	
	return f[cur] = size[cur] * res % MOD;
}
int ans;
void dfs2(int u) {
	if(fa[u]) {
		son[u].pb(g[u]);sort(son[u].begin(),son[u].end());
	}
	int up = son[u].size();
	sl[u].resize(up);sl[u][0] = son[u][0]; 	
	for(int i = 1; i<up; i++) {//好像不太能把初始化合并进来 
		sl[u][i] = (sl[u][i-1] * seed + son[u][i])%MOD;
	}
	sr[u].resize(up);sr[u][up-1] = son[u][up-1];
	for(int i = up-2; i>=0; i--) sr[u][i] = (sr[u][i+1] + son[u][i] * PW[up-i-1])%MOD; //其实不是求后缀的HASH值，而是前缀HASH的后缀和，所以要这么写 
	for(int i = head[u]; ~i; i = e[i].ne) {
		int v = e[i].v;if(v == fa[u]) continue;
		if(up == 1) {g[v] = 1; dfs2(v); break;}
		int p = lower_bound(son[u].begin(),son[u].end(),f[v]) - son[u].begin();
		g[v] = 0;
		if(p+1 < up) g[v] = sr[u][p+1];
		if(p-1 >= 0) g[v] = (g[v]+sl[u][p-1]*PW[up-1-p])%MOD;
		g[v] = g[v] * (n-size[v]) % MOD;
		if(isB && deg[v] == 1 && vis.find(g[v]) != vis.end()) ans = min(ans, v);
		dfs2(v);
	}
	if(!isB) vis.insert(sl[u][up - 1] * n % MOD);
}
int main()
{
	PW[0] = 1;
	for(int i = 1; i<MAX; i++) PW[i] = PW[i-1]*seed % MOD;
	cin>>n;
	memset(head,-1,sizeof head);
	for(int u,v,i = 1; i<n; i++) {
		cin>>u>>v;
		add(u,v);add(v,u);
	}
	dfs1(1,0);  dfs2(1);
	tot=0,isB=1,n++;
	memset(head,-1,sizeof head);
	for(int u,v,i = 1; i<n; i++) {
		cin>>u>>v;
		add(u,v);add(v,u);
	} 
	dfs1(1,0);
	ans=1e9;
	if(deg[1] == 1 && vis.find(f[e[head[1]].v]) != vis.end()) 
		ans = 1;
	dfs2(1);
	printf("%d\n",ans); 
	return 0 ;
}

另一种及其简单的Hash方式：

我们只需要 $H_u = seed \times( \prod H_{v_i} + size[u])$ 就可以了。

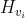其中 $H_{v_i}$ 是每一个子树的hash值
这个函数和上一个函数一样，支持换根，那么就不限于找重心了
那第一颗树所有的hash值丢进set中，第二颗树删除一个节点的hash值也可以用类似的方法弄出来。

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<queue>
#include<map>
#include<vector>
#include<set>
#include<string>
#include<cmath>
#include<cstring>
#define F first
#define S second
#define ll long long
#define pb push_back
#define pm make_pair
using namespace std;
typedef pair<int,int> PII;
const int MAX = 2e5 + 5;
//const ll MOD = 2000020331;//这个模数在这个方法中可以直接扔掉了，因为根本不是质数所以肯定要不了，因为逆元的求法就不对。
const ll MOD = 2000004199;  //用这个模数都没有问题！
const ll seed = 13331;//可换！ 233,2333,23333对于第二个模数都可以过
ll INV;
struct Edge {
	int v,ne;
} e[MAX];
int head[MAX],tot;
int n;
void adde(int u,int v) {
	e[++tot].v = v;
	e[tot].ne = head[u]; head[u] = tot;
}
inline ll qpow(ll a,ll b) {
	ll res = 1;
	while(b) {
		if(b&1) res = res * a % MOD;
		a = a *a % MOD;
		b >>= 1;		
	}
	return res;
}
inline ll add(ll x,ll y) {return (x+y)%MOD;}
inline ll mul(ll x,ll y) {return (x*y)%MOD;}
inline ll sub(ll x,ll y) {return (x-y+MOD)%MOD;}
ll H[MAX];
int size[MAX],du[MAX];
void dfs(int cur,int fa) {
	H[cur] = 1;size[cur] = 1;
	for(int i = head[cur]; ~i; i = e[i].ne) {
		int v = e[i].v;
		if(v == fa) continue;
		dfs(v,cur);
		size[cur] = add(size[cur],size[v]);
		H[cur] = mul(H[cur],H[v]);
	}
	H[cur] = add(H[cur],size[cur]);
	H[cur] = mul(H[cur],seed);
}
set<ll> ss;
bool isB;
void dfs1(int cur,int fa) {
	if(isB==0) ss.insert(H[cur]);//必须要先插入，因为根的情况。 
	ll Hall = mul(H[cur],INV),Hres;
	Hall = sub(Hall,n);
	for(int i = head[cur]; ~i; i = e[i].ne) {
		int v = e[i].v;
		if(v == fa) continue;
		Hres=mul(Hall,qpow(H[v],MOD-2));
		Hres=add(Hres,n-size[v]); Hres=mul(Hres,seed);
		//至此Hres代表除v的树的Hash值
		H[v]=mul(H[v],INV); H[v]=sub(H[v],size[v]);
		H[v]=mul(H[v],Hres);H[v]=add(H[v],n);H[v]=mul(H[v],seed);
		dfs1(v,cur);
	}
}
int main()
{
	INV = qpow(seed,MOD-2);
	cin>>n;
	tot=0;
	memset(head,-1,sizeof head);
	for(int u,v,i = 1; i<n; i++) scanf("%d%d",&u,&v),adde(u,v),adde(v,u);
	dfs(1,0);
	dfs1(1,0);
	tot=0;
	memset(head,-1,sizeof head);
	n++;
	for(int u,v,i = 1; i<n; i++) {
		scanf("%d%d",&u,&v);
		du[u]++,du[v]++;
		adde(u,v);adde(v,u);
	}
	isB=1;
	dfs(1,0);
	dfs1(1,0);
	for(int i = 1; i<=n; i++) {
		if(du[i] == 1) {
			ll Hres = mul(H[i],INV);
			Hres = sub(Hres,n);
			if(ss.find(Hres) != ss.end()) {
				printf("%d\n",i);return 0 ;
			}
		}
	}
	return 0 ;
}