离散数学谓词逻辑

命题逻辑的推理理论

推理的基本概念：设Ｇ，Ｈ是公式，对任意解释Ｉ，如果Ｉ满足Ｇ，那么Ｉ满足Ｈ，则称Ｈ是Ｇ的逻辑
结果（或称Ｇ蕴涵Ｈ），记为Ｇ⇒Ｈ，此时称Ｇ为前提，Ｈ为结论。
推广：设Ｇ１，Ｇ２，…，Ｇｎ，Ｈ是公式，称Ｈ是Ｇ１，Ｇ２，…，Ｇｎ的逻辑结果（Ｇ１，Ｇ２，…，Ｇｎ共同蕴涵Ｈ），当
且仅当（Ｇ１∧Ｇ２∧…∧Ｇｎ）→Ｈ为永真式，记为Ｇ１，Ｇ２，…，Ｇｎ⇒Ｈ，称Ｇ１，Ｇ２，…，Ｇｎ称为一组前提，用集合Г来表示，记Г＝｛Ｇ１，Ｇ２，…，Ｇｎ｝。Ｈ称为结论，则可简记记为Г⇒Ｈ

推理规则：
①规则Ｐ（称为前提引用规则）：在推导的过程中，可随时引入前提集合中的任意一个前提；
②规则Ｔ（逻辑结果引用规则）：在推导的过程中，可以随时引入公式Ｓ，该公式Ｓ是由其前的一个或多个公式推导出来的逻辑结果。
③规则ＣＰ（附加前提规则）：如果能从给定的前提集合Г与公式Ｐ推导出Ｓ，则能从此前提集合Г推导出Ｐ→Ｓ。

谓词

１．谓词的概念与表示
在谓词逻辑中，原子命题分解成个体词和谓词．
·个体词
是可以独立存在的客体，它可以是具体事物或抽象的概念
个体词分个体常量（用ａ，ｂ，ｃ，…表示）和个体变量（用ｘ，ｙ，ｚ，…表示）；
·谓词
是用来刻划个体词的性质或事物之间关系的词．
含ｎ个个体词的谓词称ｎ元谓词。
２．命题函数与量词
·（简单）命题函数
即“谓词（若干客体变项）”。
逻辑符号化

例　用谓词逻辑符号化下述语句：
（１）天下乌鸦一般黑；
（２）在美国留学的学生未必都是亚洲人；
（３）每个实数都存在比它大的另外的实数；
（４）尽管有人很聪明，但未必一切人都聪明；
解：（１）天下乌鸦一般黑

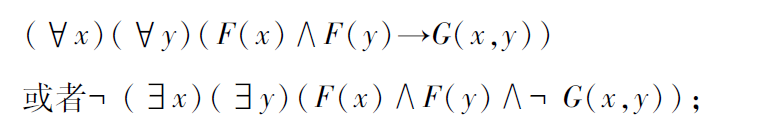
（２）在美国留学的学生未必都是亚洲人
设Ａ（ｘ）：ｘ是亚洲人；Ｈ（ｘ）：ｘ是在美国留学的学生，

（３）每个实数都存在比它大的另外的实数
设Ｒ（ｘ）：ｘ是实数；Ｌ（ｘ，ｙ）：ｘ小于ｙ，则：

（４）尽管有人很聪明，但未必一切人都聪明
设Ｍ（ｘ）：ｘ是人；Ｃ（ｘ）：ｘ很聪明，则：

知识点２　谓词公式与解释、变元的约束
１．谓词公式与解释
·原子公式
若Ｐ（ｘ１，ｘ２，…，ｘｎ）是ｎ元谓词，ｔ１
，ｔ２
，…，ｔｎ
是项，则称Ｐ（ｔ１，ｔ２，…，ｔｎ）为原子谓词公式，简称原子公式；
·谓词公式
满足下列条件的表达式，称为合式公式，简称公式。
①原子公式是合式公式；
②若Ｇ，Ｈ是合式公式，则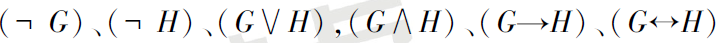

也是合式公式；
③若Ｇ是合式公式，ｘ是个体变量，则

Ｇ也是合式公式；
④仅仅由① －③产生的表达式才是合式公式。