Reed-Solomon-RS码详解

一、参数简要介绍

当我们要传输$k$比特数据的时候，我们编码后的码字长为$n=k+2s$，该码可纠$s$位错。最常用的参数设置为：$k=223,s=16,n=k+2s=255$。

二、思路

对于$k$位数据$m_0,...,m_{k-1}$，我们可以将其表示为多项式的形式$m(x)=m_0+m_{1}x+...+m_{k-1}{x}^{k-1}$。然后我们可以找$n$个不同的$x_i$，分别带入$m(x)$中，计算得到$(x_0,y_0),...(x_{n-1},y_{n-1})$。
在所有$(y_0,...y_{n-1})$中最多有$s$个错误。因此我们找一个$k+s$多的子集。这个子集能够包含$k$个正确的点。然后求出一条符合这些点的多项式。后面我们将考虑如何求这个子集的问题。

假设我们拿到了$k$个正确的值，我们怎么回复这个多项式呢？拉格朗日插值或者解方程组！下图给出了解方程组的方法：

三、具体算法

在具体实现中，取$GF(2^r)$的本原元$\alpha$，然后定义一个生成多项式：
$$g(x)=(x-\alpha )(x-{\alpha }^2)...(x-{\alpha }^{2s-1})$$
然后我们将我们的消息$m(x)=m_0+m_{1}x+...+m_{k-1}{x}^{k-1}$做下面的运算：
$$b(x)=x^{2s}m(x)(modg(x))(式1)$$

(式1)就表示了$x^{2s}m(x)=q(x)g(x)+b(x)$的关系。我们最后的码字就是：
$$c(x)=x^{2s}m(x)-b(x)$$

$c(x)=x^{2s}m(x)-b(x)$
$=q(x)g(x)+b(x)-b(x)$
$=q(x)g(x)$

下面我们来具体看一下上面的变化是如何形成码字：
首先消息为$(m_{k-1},....,m_0)$
$x^{2s}m(x)$就是将嘻嘻移位$2s$位：$(m_{k-1},....,m_0,0,...,0)$(2s个0)
$c(x)=x^{2s}m(x)-b(x)$的操作就得到了码字$c(x)$：
$(m_{k-1},....,m_0,-b_{2s-1},...,-b_0)$

当我们想检查码字是不是正确的，就将他$mod(g(x))$。如果正确，我们取码字前$k$位即可。

四、引理证明

1.对任意$g(x)$的根$\beta$，${\beta }^{2s}m(\beta )=b(\beta )$。

因为$x^{2s}m(x)=q(x)g(x)+b(x)$，所以${\beta }^{2s}m(\beta )=q(\beta )g(\beta )+b(\beta )=b(\beta )$。
因为$g(x)=(x-\alpha )(x-{\alpha }^2)...(x-{\alpha }^{2s-1})$，所以有${\alpha }^{j\cdot 2s}m({\alpha }^j)=b({\alpha }^j),1\le j\le 2s$。

2.任意给定总共$k$位$m(x)$和$b(x)$的系数。我们可以正确恢复$m(x)$和$b(x)$所有系数。
$g(x)$度数为$2s$，所以$b(x)$有$2s=n-k$个系数。$m(x)$有k个系数，所以$c(x)$有$n$个系数。给定其中k个后，还剩$n-k=2s$个位置参数，利用引理1构建以下方程组：

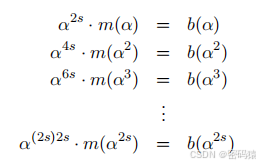
$2s$个方程组解$2s$个未知数，成功恢复所有参数。

3.假设$m(x),b(x)$存在$s$位错误系数，那么我们可以正确恢复$m(x)$所有系数。

正如前面我们讲的，最多$s$为错误，那么至少有$k+s$正确。假设我们找到包含$k+s$个点的子集，那么至少有$k$个点正确，就可以利用前面的引理正确恢复所有参数。

五、译码

假设收到了$r(x)=c(x)+e(x)$:

1. 计算$s_i=r({\alpha }^i),1\le i\le 2s$。
2. 利用Berlekamp算法定位错误。
3. 然后就可以利用前面的算法恢复出消息。